В данной работе строится FP//LINSPACE алгоритмический аналог вещественной функции Римана ![]() для алгоритмических вещественных чисел
для алгоритмических вещественных чисел ![]() ,
, ![]() , с полиномиальной временной и линейной емкостной сложностью на машине Тьюринга в модели Ко-Фридмана алгоритмических чисел и функций. Для построения алгоритмического аналога функции Римана
, с полиномиальной временной и линейной емкостной сложностью на машине Тьюринга в модели Ко-Фридмана алгоритмических чисел и функций. Для построения алгоритмического аналога функции Римана ![]() предлагается алгоритм расчета двоично-рациональных приближений данной функции для вещественных
предлагается алгоритм расчета двоично-рациональных приближений данной функции для вещественных ![]() ,
, ![]() , с полиномиальной временной и линейной емкостной сложностью на машине Тьюринга. Данный алгоритм строится на основе разложения в числовой ряд, который сходится для вещественных
, с полиномиальной временной и линейной емкостной сложностью на машине Тьюринга. Данный алгоритм строится на основе разложения в числовой ряд, который сходится для вещественных ![]() ,
, ![]() , при этом показывается и используется в данном алгоритме линейная сходимость числового ряда. Предложенный алгоритм вычисления вещественной функции Римана
, при этом показывается и используется в данном алгоритме линейная сходимость числового ряда. Предложенный алгоритм вычисления вещественной функции Римана ![]() включает использование алгоритмов вычисления вещественной функции
включает использование алгоритмов вычисления вещественной функции ![]() и гипергеометрических рядов с полиномиальным временем и линейной памятью. Предложенный алгоритм (модифицированный некоторым образом для работы с комплексными числами) может использоваться для вычисления комплексной функции Римана
и гипергеометрических рядов с полиномиальным временем и линейной памятью. Предложенный алгоритм (модифицированный некоторым образом для работы с комплексными числами) может использоваться для вычисления комплексной функции Римана ![]() для
для ![]() ,
, ![]() (то есть также для
(то есть также для ![]() ), с использованием полиномиального времени и линейной памяти по
), с использованием полиномиального времени и линейной памяти по ![]() , где
, где ![]() – точность вычислений. Модифицированный алгоритм также будет использовать полиномиальное время и линейную память по
– точность вычислений. Модифицированный алгоритм также будет использовать полиномиальное время и линейную память по ![]() и экспоненциальное время и экспоненциальную память по
и экспоненциальное время и экспоненциальную память по ![]() .
.
В данной работе рассматриваются алгоритмические (вычислимые) вещественные числа и функции, которые представляются функциями Коши, вычислимыми на машине Тьюринга [1] (такая модель алгоритмических чисел и функций называется моделью Ко-Фридмана).
Основные результаты по теории алгоритмических чисел и функций и их вычислительной сложности находятся, например, в [1]; основные результаты по теории вычислительной сложности на машине Тьюринга находятся, например, в [2].
Известно, что вещественная функция Римана ![]() [3] является полиномиально вычислимой по времени для натуральных
[3] является полиномиально вычислимой по времени для натуральных ![]() [4, 5]; алгоритмы из [4, 5] требуют не менее чем
[4, 5]; алгоритмы из [4, 5] требуют не менее чем ![]() ячеек памяти для вычисления приближенных значений функции
ячеек памяти для вычисления приближенных значений функции ![]() с точностью
с точностью ![]() . Также имеется алгоритм вычисления гипергеометрических рядов с произвольной точностью с квази-линейным временем и линейной памятью [6], который применим к вычислению значения
. Также имеется алгоритм вычисления гипергеометрических рядов с произвольной точностью с квази-линейным временем и линейной памятью [6], который применим к вычислению значения ![]() . Временная и емкостная вычислительная сложность алгоритмов из [4, 5, 6] рассматривается в контексте битовой сложности; на машине Тьюринга алгоритмы из [4, 5] являются полиномиальными по времени и квази-линейными по памяти, а алгоритм из [6] является полиномиальным по вроемени и линейным по памяти.
. Временная и емкостная вычислительная сложность алгоритмов из [4, 5, 6] рассматривается в контексте битовой сложности; на машине Тьюринга алгоритмы из [4, 5] являются полиномиальными по времени и квази-линейными по памяти, а алгоритм из [6] является полиномиальным по вроемени и линейным по памяти.
В данной работе показывается, что вещественная функция Римана ![]() является полиномиально вычислимой по времени и линейно вычислимой по памяти (с помощью одного и того же алгоритма) на машине Тьюринга для вещественных
является полиномиально вычислимой по времени и линейно вычислимой по памяти (с помощью одного и того же алгоритма) на машине Тьюринга для вещественных ![]() ,
, ![]() , в модели Ко-Фридмана. Для доказательства данного результата строится алгоритм вычисления вещественной функции Римана
, в модели Ко-Фридмана. Для доказательства данного результата строится алгоритм вычисления вещественной функции Римана ![]() с полиномиальным временем и линейной памятью на машине Тьюринга. Данный алгоритм основан на разложении функции Римана
с полиномиальным временем и линейной памятью на машине Тьюринга. Данный алгоритм основан на разложении функции Римана ![]() в числовой ряд [7, 8] для комплексных
в числовой ряд [7, 8] для комплексных ![]() ,
, ![]() ; в данном алгоритме используются алгоритмы из [9, 10, 11] вычисления вещественной функции
; в данном алгоритме используются алгоритмы из [9, 10, 11] вычисления вещественной функции ![]() и гипергеометрических рядов с полиномиальным временем и линейной памятью. Для построения алгоритма вычисления функции Римана
и гипергеометрических рядов с полиномиальным временем и линейной памятью. Для построения алгоритма вычисления функции Римана ![]() используются алгоритм вычисления числовых рядов из [12] и прямой и обратный анализ ошибок округления в численных алгоритмах [9, 10, 11, 13].
используются алгоритм вычисления числовых рядов из [12] и прямой и обратный анализ ошибок округления в численных алгоритмах [9, 10, 11, 13].
Частично результат, изложенный в данной работе, представлялся на научной конференции «Научная дискуссия: вопросы математики, физики, химии, биологии» [14].
1.1 ![]() алгоритмические числа и функции
алгоритмические числа и функции
Функции Коши в модели Ко-Фридмана [1] – это функции, двоично-рационально сходящиеся к вещественным числам. Фукнция ![]() (здесь
(здесь ![]() – множество двоично-рациональных чисел) двоично-рационально сходится к вещественному числу
– множество двоично-рациональных чисел) двоично-рационально сходится к вещественному числу ![]() , если
, если ![]() для всех
для всех ![]() ; с помощью
; с помощью ![]() обозначается множество всех функций, двоично-рационально сходящихся к числу
обозначается множество всех функций, двоично-рационально сходящихся к числу ![]() .
.
Definition 1. [1] Вещественное число ![]() называется
называется ![]() алгоритмическим вещественным число, если
алгоритмическим вещественным число, если ![]() содержит функцию
содержит функцию ![]() , вычислимую на машине Тьюринга.
, вычислимую на машине Тьюринга.
Definition 2. [1] Вещественная функция ![]() , заданная на отрезке
, заданная на отрезке ![]() , называется
, называется ![]() алгоритмической вещественнойфункцией на отрезке
алгоритмической вещественнойфункцией на отрезке ![]() , если существует машина Тьюринга
, если существует машина Тьюринга ![]() с оракульной функцией такая, что для всех
с оракульной функцией такая, что для всех ![]() и для всех
и для всех ![]() функция
функция ![]() , вычисляемая машиной
, вычисляемая машиной ![]() с оракульной функцией
с оракульной функцией ![]() , принадлежит
, принадлежит ![]() .
.
1.2 Вычислительная сложность алгоритмических функций
Definition 3. [1] Фукнция ![]() называется
называется ![]() вычислимой по времени вещественной функцией на отрезке
вычислимой по времени вещественной функцией на отрезке ![]() , если для всех алгоритмических вещественных чисел
, если для всех алгоритмических вещественных чисел ![]() функция
функция ![]() (
(![]() берется из определения
берется из определения ![]() алгоритмических вещественных функций) является
алгоритмических вещественных функций) является ![]() вычислимой по времени.
вычислимой по времени.
Definition 4. [1] Функция ![]() называется
называется ![]() вычислимой по памяти вещественной функцией на отрезкеl
вычислимой по памяти вещественной функцией на отрезкеl ![]() , если для всех алгоритмических вещественных чисел
, если для всех алгоритмических вещественных чисел ![]() функция
функция ![]() (
(![]() берется из определения
берется из определения ![]() алгоритмических вещественных функций) является
алгоритмических вещественных функций) является ![]() вычислимой по памяти.
вычислимой по памяти.
Входными данными функций ![]() и
и ![]() является запись
является запись ![]() (повторение данного символа
(повторение данного символа ![]() раз) в случае, когда функции вычисляются с точностью
раз) в случае, когда функции вычисляются с точностью ![]() .
.
С помощью FP//LINSPACE обозначается класс строковых функций, вычислимых за полиномиальное время и линейную память (с помощью одного и того же алгоритма) на машине Тьюринга. Полиномиально вычислимые по времени и линейно вычислимые по памяти алгоритмические вещественные числа и функции называются FP//LINSPACE алгоритмическими вещественными функциями. Множество FP//LINSPACE алгоритмических вещественных функций на отрезке ![]() обозначается с помощью FP//LINSPACE
обозначается с помощью FP//LINSPACE![]() .
.
1.3 Вычисление приближений вещественных функций
В данной работе используются следующие результаты из [9, 10, 11].
Для умножения ![]() и
и ![]() с точностью
с точностью ![]() , где
, где ![]() и
и ![]() – вещественные числа такие, что
– вещественные числа такие, что ![]() и
и ![]() для некоторого натурального числа
для некоторого натурального числа ![]() , достаточно вычислять
, достаточно вычислять ![]() и
и ![]() с точностью
с точностью ![]() для
для ![]() , где
, где ![]() – линейная функция натуральных аргументов.
– линейная функция натуральных аргументов.
Для вычисления величины, обратной к ![]() с точностью
с точностью ![]() , где
, где ![]() – вещественное число такое, что
– вещественное число такое, что ![]() для некоторого натурального числа
для некоторого натурального числа ![]() , достаточно вычислять
, достаточно вычислять ![]() с точностью
с точностью ![]() для
для ![]() , где
, где ![]() – линейная функция натуральных аргументов.
– линейная функция натуральных аргументов.
Для вычисления функции ![]() с точностью
с точностью ![]() , где вещественные
, где вещественные ![]() и вещественное число
и вещественное число ![]() , достаточно вычислять
, достаточно вычислять ![]() и
и ![]() с точностью
с точностью ![]() для
для ![]() , где
, где ![]() – линейная функция натуральных аргументов.
– линейная функция натуральных аргументов.
Можно показать, что для вычисления функции ![]() с точностью
с точностью ![]() , где вещественные
, где вещественные ![]() и вещественное
и вещественное ![]() , достаточно вычислять
, достаточно вычислять ![]() с точностью
с точностью ![]() для
для ![]() , где
, где ![]() – линейная функция натуральных аргументов.
– линейная функция натуральных аргументов.
2 FP//LINSPACE вычисление функции ![]()
Рассмотрим числовой ряд [7, 8] фунции Римана ![]() , сходящийся для всех комплексных чисел
, сходящийся для всех комплексных чисел ![]() (исключая
(исключая ![]() для целых
для целых ![]() ):
):
![]() (1)
(1)
Пусть
![]()
![]()
![]()
![]() и
и
![]()
запишем ряд (1) следующим образом:
![]() (2)
(2)
Пусть ![]() – натруальное число,
– натруальное число, ![]() ; пусть
; пусть ![]() и
и ![]() – натуральное число такое, что
– натуральное число такое, что ![]() . Будем вычислять
. Будем вычислять ![]() по формуле (2) с точностью
по формуле (2) с точностью ![]() для таких
для таких ![]() , где
, где ![]() – натуральное число.
– натуральное число.
2.1 Вычисление ![]()
Так как
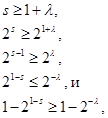 (3)
(3)
выполняютя соотношения
![]()
![]()
![]()
Следовательно
![]() ,
,
где ![]() – некторая константа (следует из соотношений, изложенных в параграфе 2.2.3).
– некторая константа (следует из соотношений, изложенных в параграфе 2.2.3).
Это означает, что для вычисления ![]() по формуле (2) с точностью
по формуле (2) с точностью ![]() достаточно вычислять величины
достаточно вычислять величины ![]() и
и ![]() с точностью
с точностью ![]() , где
, где ![]() (
(![]() – константа, зависящая от
– константа, зависящая от ![]() ).
).
Далее, для вычисления величины ![]() с точностью
с точностью ![]() воспользуемся алогитмом из [9, 10, 11] вычисления функции
воспользуемся алогитмом из [9, 10, 11] вычисления функции ![]() с точностью
с точностью ![]() ; при этом достаточно вычислять величину
; при этом достаточно вычислять величину ![]() до точности
до точности ![]() для
для ![]() , где
, где ![]() – линейная функция натуральных аргументов (
– линейная функция натуральных аргументов (![]() – некоторое натуральное число).
– некоторое натуральное число).
2.2 Вычисление ![]()
Будем вычислять функцию ![]() следующим образом:
следующим образом:
1) вычисляем ![]() с точностью
с точностью ![]() ;
;
2) вычисляем ![]() с точностью
с точностью ![]() ;
;
3) вычисляем
![]() ,
,
где ![]() и
и ![]() – приближенные значения величин
– приближенные значения величин ![]() and
and ![]() соответственно с точностью
соответственно с точностью ![]() ; пусть
; пусть ![]() – точность вычисления величины
– точность вычисления величины ![]() ;
;
4) вычисляем
![]()
пусть ![]() – точность вычисления величины
– точность вычисления величины ![]() .
.
Для вычисления величины ![]() с точностью
с точностью ![]() воспользуемся алгоритмом из [9, 10, 11] вычисления функции
воспользуемся алгоритмом из [9, 10, 11] вычисления функции ![]() с точностью
с точностью ![]() ; для этого достаточно вычислять величину
; для этого достаточно вычислять величину ![]() с точностью
с точностью ![]() для
для ![]() , где
, где ![]() – это линейная функция натуральных аргументов (
– это линейная функция натуральных аргументов (![]() – натуральное число).
– натуральное число).
Следовательно, для вычисления величины ![]() с точностью
с точностью ![]() с помощью суммирования ряда величину
с помощью суммирования ряда величину ![]() достаточно вычислять с точностью
достаточно вычислять с точностью ![]() , где
, где ![]() .
.
2.2.1 Вычисление ![]()
Запишем величину ![]() следующим образом:
следующим образом:
![]()
Будем вычислять ![]() в цикле по
в цикле по ![]() , на каждом шаге вычисляя
, на каждом шаге вычисляя
![]()
(при этом ![]() ), где
), где ![]() – приближенное значение величины
– приближенное значение величины ![]() с точностью
с точностью ![]() ,
, ![]() – приближенное значение величины
– приближенное значение величины ![]() с точностью
с точностью ![]() ;
; ![]() для всех натуральны
для всех натуральны ![]() . Будем вычислять
. Будем вычислять ![]() с точностью
с точностью ![]() , отбрасывая все биты после точки, начиная с
, отбрасывая все биты после точки, начиная с ![]() -го бита.
-го бита.
Используя метод математической индукции по ![]() , покажем, что
, покажем, что ![]() для каждого
для каждого ![]() , если брать
, если брать ![]() .
.
База индукции: ![]() ; в этом случае, величина
; в этом случае, величина ![]() , равнаяo
, равнаяo ![]() , вычисляется с точностью
, вычисляется с точностью ![]() . Индукционный рпереход: пусть
. Индукционный рпереход: пусть ![]() для
для ![]() . В этом случае
. В этом случае
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
(здесь используется оценка ![]() ). Следовательно, выполняется оценка
). Следовательно, выполняется оценка
![]()
в частности, ![]() . Это означает, что достаточно брать
. Это означает, что достаточно брать ![]() и
и ![]() для вычисления
для вычисления ![]() с точностью
с точностью ![]() . И, далее, для вычисления
. И, далее, для вычисления ![]() с точностью
с точностью ![]() достаточно брать
достаточно брать ![]() где
где ![]() – линейная функция натурального аргумента, так как
– линейная функция натурального аргумента, так как ![]() .
.
2.2.2 Вычисление ![]()
Будем вычислять ![]() в цикле по
в цикле по ![]() . Так как
. Так как
![]()
![]()
где ![]() и
и ![]() , выполняется соотношение
, выполняется соотношение
![]()
![]()
Далее, из
![]()
следует
![]()
Следовательно, если взять ![]() и вычислять
и вычислять ![]() и
и ![]() с точностью
с точностью ![]() , то точность вычисления
, то точность вычисления ![]() будет
будет ![]() .
.
Найдем точность вычисления of ![]() используя следующие соотношения:
используя следующие соотношения:
![]()
где
![]() и
и ![]()
Так как
![]()
выполняется соотношение
![]()
Оценим сверху величину
![]()
Пусть ![]() – нечетное натуральное число и
– нечетное натуральное число и ![]() ; пусть
; пусть
![]()
Так как ![]() , выполняются равенства
, выполняются равенства
![]()
![]()
![]()
Следовательно,
![]()
![]() и
и ![]()
из чего получаем
![]() и
и ![]()
(те же самые соотношения выполняются в случае, когда ![]() – четное). Следовательно
– четное). Следовательно
![]()
Как результат, если взять ![]() , то
, то
![]()
Это означает, что достаточно взять ![]() и
и ![]() для вычисления
для вычисления ![]() с точностью
с точностью ![]() .
.
3 Основной результат
Как результат, получаем, что для вычисления ![]() с точностью
с точностью ![]() для
для ![]() достаточно выполнить следующие шаги:
достаточно выполнить следующие шаги:
1) вычислить ![]() с точностью
с точностью ![]() для
для ![]() где
где ![]() – линейная функция натуральных аргументов, и
– линейная функция натуральных аргументов, и
2) использовать ![]() умножений двоично-рациональных чисел длины
умножений двоично-рациональных чисел длины![]() , где
, где ![]() – линейная функция натуральных аргументов.
– линейная функция натуральных аргументов.
Следовательно выполняется следующая теорема.
Теорема 1. Вещественная функция Римана ![]() принадлежит классу FP//LINSPACE
принадлежит классу FP//LINSPACE![]() для любого интервала
для любого интервала ![]() , где
, где ![]() ,
, ![]() ,
, ![]() и
и ![]() – натуральное число,
– натуральное число, ![]() .
.
Также выполняется следующая теорема (учитывая параграф 1.3).
Теорема 2. Вещественная функция Римана ![]() является экспоненциально вычислимой по времени и экспоненциально вычислимой по памяти по
является экспоненциально вычислимой по времени и экспоненциально вычислимой по памяти по ![]() для любого отрезка
для любого отрезка ![]() , где
, где ![]() ,
, ![]() ,
, ![]() и
и ![]() – натуральное число,
– натуральное число, ![]() .
.
Рецензенты:
Косовский Н.К., д.ф.-м.н., профессор, зав. кафедрой информатики, математико-механический факультет, Санкт-Петербургский государственный университет (Министерство образования и науки Российской Федерации), г. Санкт-Петербург.
Ермаков С.М., д.ф.-м.н., профессор, зав. кафедрой статистического моделирования, математико-механический факультет, Санкт-Петербургский государственный университет (Министерство образования и науки Российской Федерации), г. Санкт-Петербург.
Библиографическая ссылка
Яхонтов С.В. ЭФФЕКТИВНОЕ ПО ВРЕМЕНИ И ПАМЯТИ ВЫЧИСЛЕНИЕ ДЗЕТА-ФУНКЦИИ РИМАНА В МОДЕЛИ КО-ФРИДМАНА // Современные проблемы науки и образования. – 2014. – № 6. ;URL: https://science-education.ru/ru/article/view?id=16788 (дата обращения: 27.04.2024).



