Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Орлова Е.Г. 1 Феоктистов Д.В. 1 Кузнецов Г.В. 1

---

1 Национальный исследовательский Томский политехнический университет

Приведены результаты экспериментального исследования влияния шероховатости поверхности и расхода жидкости на динамику изменения краевого угла при растекании капли дистиллированной воды по твердой горизонтальной поверхности медных подложек в форме круглых дисков с различной шероховатостью. Определены значения статических краевых углов для подложек с разной шероховатостью в зависимости от расхода дистиллированной воды. Установлено, что с увеличением расхода жидкости статические углы растут, а с увеличением шероховатости поверхности происходит изменение наступающих динамических краевых углов. Показано, что при больших скоростях линия трехфазного контакта не тормозится элементами шероховатости, и происходит уменьшение динамического краевого угла. При малых скоростях происходит торможение при движении через элементы шероховатости (пиннинг контактной линии).

Статья в формате PDF

573 KB

растекание

динамический краевой угол

статический краевой угол

линия трехфазного контакта

объемный расход

теневая система

Шлирин система.

1. Attinger D., Zhao Z., Poulikakos D. Experimental study of molten micro-droplet surface deposition and solidification: transient behavior and wetting angle dynamics // Heat Mass Transfer. – 2000. – V. 122. – P. 544-546.

2. Calvert P. Inkjet Printing for Materials and Devices // Chem. Mater. –2001. – V. 13. – P. 3299-3305.

3. Chinnov E. A., Kabov O. A. Features of two-phase flow in a rectangular microchannel // Technical Physics Letters. –2010. – Vol. 36. – No. 5. – Р. 468-470.

4. Evaporation dynamics of microdroplets on self-assembled monolayers of dialkyl disulfides / Li G., Flores S. M., Vavilala C. et.al. // Langmuir. – 2009. – V. 25. – PP. 13438-13447.

5. Foit J.J. Spreading under variable viscosity and time-dependent boundary conditions: estimate of viscosity from spreading experiments // Nuclear Engineering and Design. – 2004. – V. 227. – PP. 239-253.

6. Kabov O. A., Zaitsev D.V. The effect of wetting hysteresis on drop spreading under gravity // Doklady Physics. – 2013. – V.451. – PP. 37-40.

7. Kim J. Spray cooling heat transfer: The state of the art // Int J Heat Fluid Flow. – 2007. – V. 28. – P. 753-767.

8. Models for fuel droplet heating and evaporation: comparative analysis / Sazhin S.S., Kristyadi T., Abdelghaffar W.A., Heikal M.R. // Fuel. – 2006. – V. 85. – P. 1613-1630.

9. Orlova E.G, Kuznetsov G.V., Feoktistov D.М. The evaporation of the water-sodium chlorides solution droplets on the heated substrate // EPJ Web of Conferences, V. 76, 012039 (2014).

10. Wenzel R.N. Persistence of Solid Surfaces to Wetting by Water // Ind.Eng.Chem. – 1936. – V.28. – P.988.

Недостаточно полное понимание свойств трехфазной линии контакта в процессе динамического взаимодействия капли с твердой поверхностью приводит к сдерживанию развития ряда технологий при капельном охлаждении поверхностей [7], нанесении различных покрытий [1], струйной печати [2, 4], впрыскивании топлива в двигатели внутреннего сгорания [8], при добыче нефти, смазке, склеивании и пропитке различных материалов, росте биологических кристаллов.

Необходимость уменьшения характерных размеров устройств в различных отраслях техники, например, в энергетике и медицине, космической индустрии и электронике, определяет развитие исследований гидродинамики газожидкостных течений в микросистемах и микроканалах [3]. Процессы, происходящие в таких течениях, характеризуются следующими факторами: теплофизическими свойствами жидкости, удельным расходом теплоносителя, физико-химическими свойствами, микрорельефом и смачиваемостью поверхности.

Несмотря на большое количество исследователей (Т. Юнг, П.С. Лаплас, П.А. Ребиндер, Б.В. Дерягин, Р. Хоффман, Дж. Бэтчелор, О.В. Воинов, Т. Блэйк), занимающихся изучением процессов смачивания и растекания жидкостей по твердой поверхности, на сегодняшний день не разработаны основные положения теории свойств линии трехфазного контакта (ЛТФК). В научной периодической литературе отсутствуют результаты исследований систем с большим диапазоном варьирования скорости растекания ЛТФК и степени шероховатости смачиваемой поверхности.

Цель данной работы: экспериментальное изучение влияния степени шероховатости, микроструктуры поверхности и расхода жидкости на наступающий динамический краевой угол (ДКУ) в процессе растекания капли недаэрированной дистиллированной воды по твердой горизонтальной поверхности.

Экспериментальная установка

Эксперименты проведены на установке (рис. 1) с использованием теневой и шлирин систем. Концепция исследований и принцип действия приведены в [9]. Съёмка растекания капли на исследуемой поверхности проводилась одновременно с двух сторон. Камера шлирин системы использовалась для осуществления контроля за осесимметричностью капли.

Рис. 1. Оптическая схема (а) и общий вид (б) экспериментальной установки: 1, 17 – источник света; 2, 16– матовое стекло; 3 – щель;

4, 14 – коллимирующая линза; 5– подложка; 6 – конденсирующая линза; 7, 11 – непрозрачный щит с отверстием; 9 – шприцевый насос; 8, 10 – высокоскоростная камера; 12 – шлирин линза; 13 –  делитель пучка; 15 – кодирующий фильтр.

В качестве твердой поверхности использовались медные подложки в форме круглых дисков толщиной 4 мм и диаметром 54 мм. Для оценки влияния шероховатости и профиля поверхности на характеристики смачивания при растекании капли выбраны подложки с разным микрорельефом поверхности. Шероховатые поверхности получены путем бомбардировки гладкой медной поверхности частицами Al2O3  размерами 10 и 100 мкм.

В каждой подложке по центру находится отверстие диаметром 2 мм, через которое шприцевым насосом (Cole-Parmer Touch Screen) выдавливается капля объемом 0,3 мл и расходом от 0,005 мл/с до 0,16 мл/с. Таким образом, реализовался способ измерения динамических краевых углов методом “сидячей капли ”.

Процесс растекания фиксировался скоростной видеокамерой FastCAMSA1.1 model 675K-M1. Скорость видеозаписи варьировалась от 10 до 1281 кадров/сек в зависимости от расхода смачивающей жидкости. Полученные видеокадры обрабатывались при помощи программного обеспечения КРУСС, в котором использовался метод Юнга-Лапласа [6] для определения ДКУ смачивания. Данная программа распознаёт профиль капли и определяет её геометрические параметры, такие как краевой угол, диаметр основания, высота, объем, площадь поверхности и др. (рис.2).

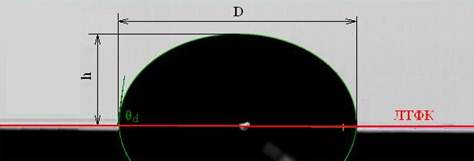
Рис. 2. Геометрические параметры капли

Основные результаты и выводы

По результатам предварительных экспериментов определены основные факторы воздействия, которые сведены в таблицу 1. Также с помощью профилометра «Micro Measure 3D station» определено среднее арифметическое отклонение профиля (Ra) на всех исследуемых подложках.

Для понимания процесса растекания жидкости по поверхности необходимо знать значение статического краевого угла на данной поверхности. В таблице 2 приведены экспериментальные данные статических краевых углов на исследуемых подложках в зависимости от объемной скорости образования капли дистиллированной воды. Статические краевые углы измерялись при постоянной смоченной площади.

Таблица 1

Основные факторы воздействия

Таблица 2

 Статические краевые углы смачивания

Установлено, что все подложки характеризуются определенными статическими углами смачивания, которые зависят от объёмной скорости образования капли. На исследуемых подложках увеличение объёмной скорости образования капли привело к увеличению статического краевого угла. Максимальное различие в значениях статических краевых углов зафиксировано на положке медь III (Ra 6,210 мкм) и составило 22°.

По результатам экспериментальных данных рассчитана скорость перемещения ЛТФК. Данная характеристика описывает скорость растекания капли по поверхности и определяется из уравнения:

где С – скорость захвата кадров, кад./с; Bd1, Bd3 – диаметр капли в предыдущий и следующий момент времени соответственно, мм; К1, К3 – номер кадра в предыдущий и следующий момент времени соответственно.

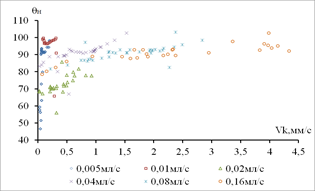
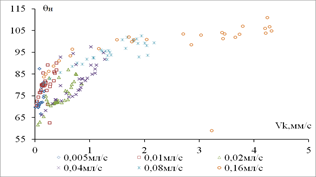
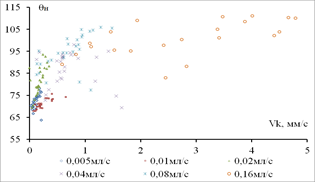
Установлено, что при растекании капли по медным подложкам, повышение шероховатости поверхности с 0,591 мкм до 5,190 мкм привело к возрастанию максимального значения наступающего краевого угла, однако последующее увеличение шероховатости до 6,210 мкм не вызвало дальнейшего роста краевого угла натекания. Максимум краевого угла натекания в 112° зафиксирован при объёмной скорости дистиллированной воды 0,160 мл/с: на меди II (Ra 5,190 мкм) (Рис. 3(б)) при скорости ЛТФК 4,250 мм/с и на меди III (Ra 6,210 мкм) в диапазоне скорости ЛТФК 2,430 – 3,480 мм/с (Рис. 3(в)). В данном случае наблюдается расхождение полученных экспериментальных результатов с результатами теоретических исследований [10], согласно которым рост краевых углов с увеличением шероховатости наблюдается на гидрофобных поверхностях (θ>90°), тогда как медные поверхности являются изначально гидрофильными (θ<90°) (табл.2). Это объясняется тем, что на краевые углы натекания влияет не только шероховатость поверхности, характеризуемая коэффициентом шероховатости K, но и форма и расположение микроканавок и микровысупов.

(а)

(б)

(в)

Рис. 3. Зависимость наступающего краевого угла от скорости перемещения ЛТФК при растекании капли дистиллированной воды по: а) отожженной меди – Ra 0,591 мкм; б) меди II – Ra 5,190 мкм; в) меди III – Ra 6.210 мкм

В данном случае шероховатость поверхностей из меди формировалась при помощи бомбардировки сферическими частицами оксида алюминия. Согласно [5] данный метод получения шероховатости поверхности является наиболее перспективным, т.к. согласно выводам автора именно такая форма микронеровностей улучшает гидрофобные свойства поверхности.

При растекании капли по медным подложкам выделено три режима. Первый режим характеризуется «скачкообразным» увеличением ДКУ натекания. Во втором режиме наступающий ДКУ монотонно уменьшается. В третьем режиме формируется равновесный краевой угол при постоянной площади смоченной поверхности.

Установлено различие в стадии «формирование равновесного краевого угла» при малых и больших скоростях роста капли. При больших скоростях роста капли (0,020–0,160 мл/с) поверхностные «дефекты» сглаживаются капиллярными волнами на поверхности жидкости, ЛТФК не зацепляется за микровыступы и ДКУ натекания уменьшается в процессе растекания. В связи с этим увеличение ДКУ при завершении процесса растекания при малых объёмных скоростях образования капли дистиллированной воды (0,005–0,010мл/с) объясняется тем, что ЛТФК капли «зацепляется» за микровыступы поверхности подложки (происходит пиннинг ЛТФК). Это приводит к увеличению ДКУ в конце процесса растекания, т.к. движущей силы потока не хватает для преодоления микровыступов.

Заключение

По результатам экспериментальных исследований получены значения статических краевых углов в зависимости от скорости образования капли дистиллированной воды на всех исследуемых поверхностях. Обнаружено, что с увеличением объемного расхода жидкости растет значение статического краевого угла на медных поверхностях. Установлено влияние шероховатости на динамический контактный угол: с ростом шероховатости увеличивается значение ДКУ натекания. Возможно, что причиной такого изменения ДКУ является не только шероховатость поверхности, но и форма и расположение микроканавок и микровысупов.

Также установлено различие в стадии «формирования равновесного краевого угла» при малых и больших расходах жидкости. При больших скоростях ЛТФК не зацепляется за микровыступы, и происходит уменьшение динамического краевого угла. При малых скоростях движущей силы потока не хватает для преодоления микровыступов, и ЛТФК «зацепляется» за неровности, происходит пиннинг контактной линии. В данном случае наблюдается увеличение ДКУ.

Работа выполнена в рамках НИР Госзадания «Наука» (шифр федеральной целевой научно-технической программы 2.1321.2014).

Заворин А.С., д.т.н., зав. каф. Парогенераторостроения и парогенераторных установок НИ ТПУ, г. Томск;

Стрижак П.А., д.ф.-м.н., профессор каф. Автоматизации теплоэнергетических процессов НИ ТПУ, г. Томск.

Библиографическая ссылка