1. исходные данные для обработки представляют собой физические параметры, характеризующиеся динамическими и распределенными свойствами;
2. вычисления производятся в реальном масштабе времени и период актуальности полученных при этом результатов ограничен;
3. в системе обрабатывается разнородная информация, т.е. вычислительный процесс характеризуется признаками гетерогенности;
4. компьютерная сеть представляет собой распределенную структуру, в которой пользовательские рабочие места могут быть разнесены по территории целой страны или даже всего земного шара;
5. такие системы должны обеспечивать распараллеливание задач для разных пользователей.
Главной проблемой создания подобных распределенных гетерогенных вычислительных систем является то, что имеющиеся комплексы уже не способны отвечать современным требованиям в плане технического, организационного, математического и программного обеспечения, так как создавались десятилетия назад [4]. Кроме того отсутствует возможность интегрирования их в единую вычислительную структуру. Отсутствие единого концептуального подхода при решении таких задач тормозит развитие информационных технологий в огромном прикладном кластере.
Разработка и совершенствование математического и алгоритмического обеспечения для решения таких задач позволит повысить эффективность работы создаваемого программного обеспечения и, как следствие, расширить область применения подобных систем.
На основе анализа программной инфраструктуры и методов обработки данных [1, 2, 5] в глобальных распределенных системах обработки данных автором предложена иерархическая структура абстрактного математического обеспечения вычислительных комплексов, предназначенного для решения задач, содержащих большой объем расчетов динамических параметров физических процессов, непрерывно проводимых в режиме реального времени. Данная иерархия представляет собой четырехуровневую структуру (рис. 1).
На низшем – четвертом уровне – рассматриваются способы (методы) вычислений, т.е. набор функций и производных с помощью которых проводятся вычисления.
Уровень определяющего параметра представлен набором параметров, которые необходимы для формирования групп вышестоящего уровня. Как правило, это индивидуальный набор значений или характеристик, получаемых в результате решения базовых математических вычислений.
Уровень группы параметров составляют базовые модели, обеспечивающие расчеты групп параметров и составление необходимых выборок гетерогенных параметров, на основе которых будут производиться вычисления.
Верхний уровень представляет собой готовую математическую модель для производства распределенных гетерогенных вычислений в глобальных компьютерных сетях, на основе данных о группах определяемых параметров.
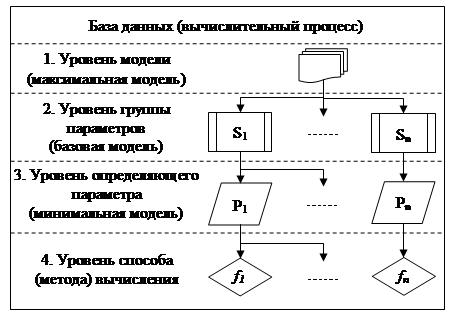
Рис. 1. Структура организации математического обеспечения систем гетерогенных распределенных вычислений динамических параметров
Показано, что предложенная иерархия математического обеспечения – это не окончательное застывшее, а постоянно развивающееся образование. На каждом этапе своего развития она представляется как частично упорядоченное множество, в котором существуют непустые подмножества как минимальных, так и максимальных элементов. Математическое моделирование при таком подходе существенно зависит от выбора конкретного класса абстрактных динамических систем, к которым и относятся вычислительные системы мониторинга глобальных физических процессов.
Параметры распределенных физических объектов и процессов носят пространственно-временной характер [3], в связи с этим, общепринято представление их характеристик в виде полей, т.е. распределенных значений в конкретный момент времени, что представляет собой достаточно большой массив данных. Чаще всего подобные массивы представляются в виде карт, показывающих привязку распределения массива данных физических параметров к географической сетке. Для производства математических операций в данном случае требуется вычисление определенных производных состояния каждого значения физического параметра в массиве. Процедура анализа конкретного значения физического показателя в массиве данных (поле) может быть сведена к разработке математической модели, основанной на решении задачи Дирихле для круга. В предложенном контексте структуры организации математического обеспечения (рис.1) уровнем максимальной модели будет являться комплексная математическая модель решения задачи Дирихле, базовыми моделями будут непосредственные наборы уравнений для расчета физических величин (давления, температуры т.д.), минимальные модели характеризуют промежуточные или производные значения, рассчитываемые для нахождения конкретных значений физических величин (лапласианы и градиенты), а уровень способа (метода) вычисления представляется набором уравнений и функций, с помощью которых осуществляются математические операции.
Суть задачи Дирихле заключается в том, что для физических параметров принимается положение, что каждая функция, которая является аналитической внутри некоторого круга с центром в точке 0, может быть описана во всех точках этого круга в следующем виде:
![]() , (1)
, (1)
Положение точки i внутри круга задается в полярных координатах следующими
параметрами: ![]() – расстояние от центральной
точки 0,
– расстояние от центральной
точки 0, ![]() – угол между прямой i и полярной осью, которая направлена с юга
на север. Если отсчет от полярной прямой ведется по ходу часовой стрелки, то
полярный угол считается положительным и наоборот.
– угол между прямой i и полярной осью, которая направлена с юга
на север. Если отсчет от полярной прямой ведется по ходу часовой стрелки, то
полярный угол считается положительным и наоборот.
Обозначив декартовы координаты произвольной точки i (xi, yi) через полярные координаты, получим:
![]() и
и ![]() , (2)
, (2)
где ![]() и
и ![]() –проекции радиус-вектора
–проекции радиус-вектора ![]() на оси x и y
соответственно.
на оси x и y
соответственно.
Интегрируя в формулу (1) значения ![]() и
выражения для
и
выражения для ![]() и
и ![]() (2),
опустив координаты центра, получим:
(2),
опустив координаты центра, получим:
![]() .
(3)
.
(3)
Аналогично, для точки i+1 получится:
![]() . (4)
. (4)
Решив систему уравнений (3)-(4), получим значения ![]() и
и ![]() :
:
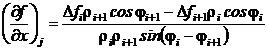 ; (5)
; (5)
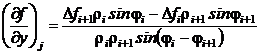 ,
(6)
,
(6)
где j = 1, 2, …, m – порядковый номер
треугольника в проекциях радиус-векторов (рисунок 2,б), по данным которого
находятся ![]() и
и ![]() .
.
Если повторить решение уравнений (5)-(6) для j = 1, 2, …, m, получим m пар значений составляющих градиента
функций ![]() . Среднее значение модуля
градиента поля
. Среднее значение модуля
градиента поля ![]() можно рассчитать из
соотношения:
можно рассчитать из
соотношения:
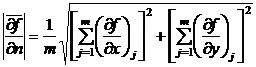 .
(7)
.
(7)
В качестве примера приведено математическое обоснование построения и анализа массива данных физических величин на основе обработки параметров давления для локального масштаба с шагом регулярной сетки от 50 до 300 км (рис.2).
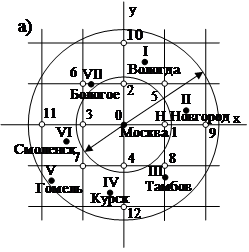
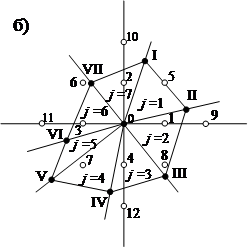
Рис.
2. Пример расположения пунктов получения данных: а) в узлах регулярной сетки,
где: ![]() – узлы метки;
– узлы метки; ![]() – пункты наблюдения; б) в
проекциях радиус-векторов
– пункты наблюдения; б) в
проекциях радиус-векторов
Таким образом, имея указанный ранее набор исходных данных, рассмотренная математическая модель способна производить расчет и построение полей любых метеорологических величин в узлах регулярной сетки. Кроме того, реализация данной модели позволит вычислять необходимые для производства дальнейших расчетов значения градиентов давления и температуры, параметров геострафического ветра, адвективных изменений некоторых метеорологических параметров, вычислять лапласиан давления и радиус кривизны изобар.
Применение данной модели в распределенной системе гетерогенных вычислений позволит отойти от загруженности серверов сети, путем кластерного распределения и управления вычислительными задачами. Это позволит проводить фрагментированную (кластерную) оценку данных с возможностью задействовать весь потенциал специализированных распределенных компьютерных сетей.
Рецензенты:Данилов А. Д., д.т.н., профессор, профессор каф. «Электропривод, автоматика и управление в технических системах», ФГБОУ ВПО «Воронежский государственный технический университет», г. Воронеж.
Барабанов В.Ф., д.т.н., профессор, профессор каф. «Автоматизированные вычислительные системы», ФГБОУ ВПО «Воронежский государственный технический университет», г. Воронеж.
Библиографическая ссылка
Пилеич А.В. МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ГЕТЕРОГЕННЫХ РАСПРЕДЕЛЕННЫХ ВЫЧИСЛЕНИЙ ДИНАМИЧЕСКИХ ПАРАМЕТРОВ ФИЗИЧЕСКИХ ПРОЦЕССОВ // Современные проблемы науки и образования. 2014. № 6. ;URL: https://science-education.ru/ru/article/view?id=16648 (дата обращения: 06.07.2025).



