В предлагаемой работе экспериментально исследуется структура и интенсивность осредненных течений изотермической жидкости, возбуждаемых в цилиндрической полости с упругой границей. Изучается влияние параметров вибраций и жидкости на структуру и интенсивность течений и закономерности их трансформации. Исследования проводятся в широком интервале значений безразмерной частоты вибраций.
1. Экспериментальная установка и методика
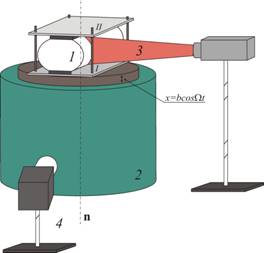
Рис. 1. Схема экспериментальной установки: 1 – кювета, 2 – электродинамический вибратор, 3 – световой нож (лазер), 4 – камера, линия n – ось вибраций.
Двумерная модель капли представляет собой
цилиндрическую полость кругового сечения длиной ![]() мм и радиусом
мм и радиусом ![]() мм (положение капли
относительно оси вибраций показано на рис. 1). Стенки кюветы изготовлены
из упругого эластичного полиэтилена, что позволяет ей сжиматься и расширяться
под действием вибрационного воздействия. Торцы кюветы герметично закрыты
фланцами из плексигласа. При заполнении кюветы рабочей жидкостью внутри нее
создается избыточное давление. Для этого в одном из торцов полости имеется
заливное отверстие с нагнетательным клапаном. В качестве рабочей жидкости
используются водоглицериновые растворы, вязкость которых варьируется в
диапазоне
мм (положение капли
относительно оси вибраций показано на рис. 1). Стенки кюветы изготовлены
из упругого эластичного полиэтилена, что позволяет ей сжиматься и расширяться
под действием вибрационного воздействия. Торцы кюветы герметично закрыты
фланцами из плексигласа. При заполнении кюветы рабочей жидкостью внутри нее
создается избыточное давление. Для этого в одном из торцов полости имеется
заливное отверстие с нагнетательным клапаном. В качестве рабочей жидкости
используются водоглицериновые растворы, вязкость которых варьируется в
диапазоне ![]() сСт
(плотность жидкости изменяется в интервале
сСт
(плотность жидкости изменяется в интервале ![]() г/см3).
г/см3).
Кювета 1
(рис. 1), заполненная рабочей жидкостью, закрепляется на столике
электродинамического вибратора 2 [2]. Конструкция крепления кюветы разработана таким
образом, что изначально полость оказывается сжатой между подвижной I
и неподвижной II пластинами-активаторами,
вследствие чего сечение кюветы принимает форму эллипса, большая ось которого ориентирована
горизонтально. Подвижная пластина I располагается
непосредственно на столике вибратора, который совершает вертикальные
гармонические колебания по закону ![]() . амплитуда и линейная частота вибраций могут
варьироваться в интервалах
. амплитуда и линейная частота вибраций могут
варьироваться в интервалах ![]() мм и
мм и ![]() Гц. В ходе опыта из-за упругих
свойств стенок вибрационное воздействие на кювету передается практически
одинаково как со стороны нижней (подвижной), так и со стороны верхней
(неподвижной) пластины. Вибрации осуществляются вдоль малых полуосей эллипса.
Эксперимент проводится при заданных значениях
Гц. В ходе опыта из-за упругих
свойств стенок вибрационное воздействие на кювету передается практически
одинаково как со стороны нижней (подвижной), так и со стороны верхней
(неподвижной) пластины. Вибрации осуществляются вдоль малых полуосей эллипса.
Эксперимент проводится при заданных значениях ![]() ,
,
![]() и f.
и f.
Для измерения вязкости жидкости используется капиллярный вискозиметр (относительная погрешность не превышает 0.1%), для измерения плотности – ареометр (с точностью 0.001 г/см3). амплитуда вибраций измеряется при помощи оптического катетометра типа В-630 (0.1 мм) или с экрана монитора при обработке видеозаписи; частота вибраций задается и контролируется универсальным измерительным комплексом ZET Lab (0.1 Гц).
Движение жидкости визуализируется светорассеивающими частицами Resine Amberlite размером 60 мкм и плотностью, близкой к плотности рабочей жидкости. Подсветка течений осуществляется световым ножом 3 (используется мощный лазер-генератор линий модели Z500Q), расположенным перпендикулярно оси вибраций. Структура течений регистрируется при помощи видеокамеры 4 (рис. 1). Поскольку движение жидкости складывается из колебательного (относительно стенок полости) и осредненного, возникающего на фоне колебаний, видеосъемка процесса осуществляется в системе отсчета полости (за счет синхронизации частоты видеосъемки с частотой вибраций полости). В зависимости от скорости осредненного движения жидкости выдержка видеосъемки изменяется в диапазоне от 1/100 до 1/1000. За это время светорассеивающие частицы на паре соседних кадров успевают «сместиться» на некоторое расстояние (рис. 2). Для вычисления распределения скоростей в пределах пары изображений и структуры осредненных течений как во всем объеме, так и в заданной точке полости используется PIV-методика, осуществляемая посредством специализированного программного обеспечения PIVlab (встраиваемый модуль MATLAB) на компьютере. Данный модуль позволяет получать, отображать и экспортировать такие параметры, как тангенциальная и касательная компоненты скорости потоков, их завихренность, дивергенция и т.д.
2. Результаты эксперимента
Вибрационное
воздействие на стенки капли вызывает колебания жидкости внутри нее, что
приводит к генерации осредненных потоков. Структура потоков и интенсивность их
осредненного движения определяются безразмерной частотой вибраций ![]() . В наших экспериментах осредненное
течение имеет двумерную структуру, представляющую собой систему вихрей,
вытянутых вдоль кюветы и согласованно вращающихся. В большинстве опытов картина
течения обладает зеркальной симметрией относительно большой и малой осей сжатой
кюветы (эллипса). Небольшое нарушение симметрии в отдельных экспериментах можно
объяснить не совсем симметричным характером вибрационного воздействия на саму
кювету. В области очень интенсивных вибраций устойчивость двумерного течения и
его симметрия нарушаются, в объеме полости возникают сложные трехмерные потоки.
. В наших экспериментах осредненное
течение имеет двумерную структуру, представляющую собой систему вихрей,
вытянутых вдоль кюветы и согласованно вращающихся. В большинстве опытов картина
течения обладает зеркальной симметрией относительно большой и малой осей сжатой
кюветы (эллипса). Небольшое нарушение симметрии в отдельных экспериментах можно
объяснить не совсем симметричным характером вибрационного воздействия на саму
кювету. В области очень интенсивных вибраций устойчивость двумерного течения и
его симметрия нарушаются, в объеме полости возникают сложные трехмерные потоки.
На рис. 2 представлены векторные поля скорости потоков (перпендикулярное сечение кюветы), возникающих в объеме жидкости, полученные при PIV-обработке видеозаписей экспериментов, проводимых при изменении вязкости жидкости и параметров вибраций.




Рис. 2. Вид и схема течений водоглицериновой смеси: а – ![]() Гц,
Гц, ![]() мм,
мм, ![]() сСт;
сСт;
б – ![]() Гц,
Гц, ![]() мм,
мм, ![]() сСт;
в –
сСт;
в – ![]() Гц,
Гц, ![]() мм,
мм, ![]() сСт;
сСт;
г – ![]() Гц,
Гц, ![]() мм,
мм, ![]() сСт.
сСт.
при
сравнительно невысоких значениях безразмерной частоты вибраций в экспериментах
с жидкостью большой вязкости (![]() сСт)
в объеме полости
формируется осредненное течение, представляющее собой систему согласованно
вращающихся вихрей (рис. 2а,
сСт)
в объеме полости
формируется осредненное течение, представляющее собой систему согласованно
вращающихся вихрей (рис. 2а,
![]() ). При этом вихри большего размера I находятся вблизи верхнего и нижнего
полюсов кюветы и вращаются согласованно друг с другом, формируя потоки,
направленные к полюсам. Можно заметить, что скорость частиц, величина которой
определяется длиной векторов, оказывается максимальной в струях, бьющих к
полюсам капли. Это значение скорости в дальнейшем будет использоваться для
числовой характеристики возникающего осредненного течения.
). При этом вихри большего размера I находятся вблизи верхнего и нижнего
полюсов кюветы и вращаются согласованно друг с другом, формируя потоки,
направленные к полюсам. Можно заметить, что скорость частиц, величина которой
определяется длиной векторов, оказывается максимальной в струях, бьющих к
полюсам капли. Это значение скорости в дальнейшем будет использоваться для
числовой характеристики возникающего осредненного течения.
Структура
осредненного течения в осциллирующей капле качественно изменяется с увеличением
безразмерной частоты вибраций: вихри I принимают вытянутую «приплюснутую»
форму и смещаются ближе к стенке кюветы. Под ними формируется новая система – «внешние»
вихри II,
имеющие противоположное направление вращения (рис. 2б, ![]() ). Картина осредненного течения
становится «двухуровневой». Повышение частоты вибраций приводит к увеличению и размера,
и интенсивности вихрей II.
). Картина осредненного течения
становится «двухуровневой». Повышение частоты вибраций приводит к увеличению и размера,
и интенсивности вихрей II.
В
случае высоких частот вибраций вихри
I,
расположенные в пограничных слоях Стокса, становятся настолько тонкими, что
оказываются практически неразличимыми (рис. 2в, ![]() ). Вихри II формируют картину, по структуре близкую
к низкочастотному случаю (рис. 2а),
но с противоположным направлением закрутки. Теперь образовавшиеся струи бьют от
полюсов кюветы, а их интенсивность близка к низкочастотному случаю.
). Вихри II формируют картину, по структуре близкую
к низкочастотному случаю (рис. 2а),
но с противоположным направлением закрутки. Теперь образовавшиеся струи бьют от
полюсов кюветы, а их интенсивность близка к низкочастотному случаю.
В
опытах с маловязкими жидкостями при интенсивном вибрационном воздействии
обнаружена неустойчивость симметричного движения, когда во всем объеме кюветы
развивается один большой центральный вихрь (рис. 2г, ![]() ).
).
для
описания и анализа экспериментальных результатов условно разделим область
безразмерных частот на низкие, ![]() ,
умеренные,
,
умеренные, ![]() ,
и высокие,
,
и высокие, ![]() .
.
В
низкочастотном диапазоне в качестве основной характеристики потока выберем скорость
струи, которая генерируется вихрями I и направлена к полюсам осциллирующей
капли. При заданной вязкости жидкости и фиксированном значении амплитуды
вибраций с повышением частоты скорость жидкости в струе ![]() увеличивается (рис. 3а). Увеличение амплитуды вибраций при постоянной
частоте также приводит к монотонному повышению скорости струи
увеличивается (рис. 3а). Увеличение амплитуды вибраций при постоянной
частоте также приводит к монотонному повышению скорости струи ![]() (рис. 3б).
(рис. 3б).
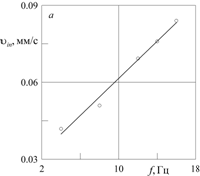
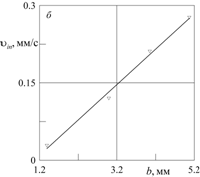
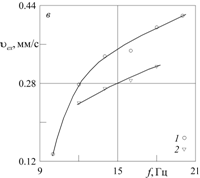
Рис. 3. Зависимость максимальной скорости ![]() струи от частоты (а, в) и амплитуды (б) вибраций: а –
струи от частоты (а, в) и амплитуды (б) вибраций: а – ![]() сСт,
сСт, ![]() мм; б –
мм; б – ![]() сСт,
сСт, ![]() Гц;
в –
Гц;
в – ![]() сСт,
сСт, ![]() мм (кривая 1),
мм (кривая 1), ![]() сСт,
сСт, ![]() мм
(кривая 2).
мм
(кривая 2).
В
области высоких и умеренных значений безразмерной частоты измерение скорости
вихрей, генерируемых в пограничных слоях, становится практически невозможным по
причине их малой толщины. Поэтому в качестве характерной скорости потоков была
выбрана скорость струи, сформированная внешними вихрями II и направленная от полюсов кюветы. При постоянном
значении вязкости ![]() сСт
скорость жидкости
сСт
скорость жидкости ![]() монотонно повышается с
увеличением частоты вибраций
монотонно повышается с
увеличением частоты вибраций ![]() (рис. 3в); амплитуда вибрационного воздействия в
ходе экспериментов поддерживается постоянной,
(рис. 3в); амплитуда вибрационного воздействия в
ходе экспериментов поддерживается постоянной, ![]() мм
(рис. 3в, кривая 1). При повышении вязкости жидкости кривая
скорости движения
мм
(рис. 3в, кривая 1). При повышении вязкости жидкости кривая
скорости движения ![]() смещается в область
меньших значений (кривая 2;
смещается в область
меньших значений (кривая 2; ![]() мм,
мм, ![]() сСт).
сСт).
3. Обсуждение результатов
В
случае высоких безразмерных частот (![]() ) определяющим вибрационным параметром
является пульсационное число Рэлея
) определяющим вибрационным параметром
является пульсационное число Рэлея ![]() [1], которое
в условиях нашей задачи примет вид
[1], которое
в условиях нашей задачи примет вид ![]() . Течение,
возникающее в объеме кюветы, генерируется за счет касательных к поверхности
осредненных потоков, формирующихся на внешней границе слоя Стокса, и увлекающих
за собой остальной объем жидкости. Безразмерная скорость осредненного течения в
объеме полости
. Течение,
возникающее в объеме кюветы, генерируется за счет касательных к поверхности
осредненных потоков, формирующихся на внешней границе слоя Стокса, и увлекающих
за собой остальной объем жидкости. Безразмерная скорость осредненного течения в
объеме полости ![]() пропорциональна
пропорциональна ![]() [3; 6].
[3; 6].
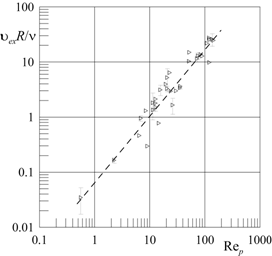
Рис. 4. Зависимость безразмерной скорости струи ![]() от
от ![]() ;
;
![]() Гц,
Гц, ![]() мм,
мм,
![]() сСт.
сСт.
На
рис. 4 представлена экспери-ментальная зависимость безразмерной скорости ![]() внешних потоков (струй), направленных
от полюсов кюветы, построенная по результатам опытов с жидкостями различной вязкости
при варьировании параметров вибраций (
внешних потоков (струй), направленных
от полюсов кюветы, построенная по результатам опытов с жидкостями различной вязкости
при варьировании параметров вибраций (![]() ).
результаты находятся в хорошем
согласии между собой на плоскости управляющих параметров
).
результаты находятся в хорошем
согласии между собой на плоскости управляющих параметров ![]() . Безразмерная скорость монотонно
возрастает с повышением пульсационного числа Релея, тем самым доказывая, что полученные
результаты соответствуют области высокочастотной асимптотики.
. Безразмерная скорость монотонно
возрастает с повышением пульсационного числа Релея, тем самым доказывая, что полученные
результаты соответствуют области высокочастотной асимптотики.
Для
характеристики скорости потоков введем безразмерный параметр ![]() [1], где в качестве единицы измерения
выбрана скорость осредненного движения жидкости, возбуждаемого в неоднородном
слое Стокса при
[1], где в качестве единицы измерения
выбрана скорость осредненного движения жидкости, возбуждаемого в неоднородном
слое Стокса при ![]() . В случае высоких
безразмерных частот в условиях ламинарного течения (область малых
. В случае высоких
безразмерных частот в условиях ламинарного течения (область малых ![]() ) параметр
) параметр ![]() не
должен изменяться с частотой. экспериментальные
результаты удовлетворительно согласуются на плоскости
не
должен изменяться с частотой. экспериментальные
результаты удовлетворительно согласуются на плоскости ![]() (рис. 5а). Параметр Vex монотонно повышается с увеличением
(рис. 5а). Параметр Vex монотонно повышается с увеличением ![]() , асимптотически приближаясь к постоянному
значению в области
, асимптотически приближаясь к постоянному
значению в области ![]() .
.
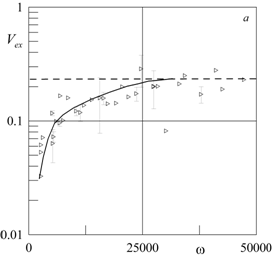
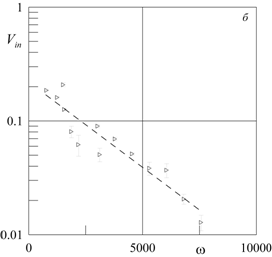
Рис. 5. Зависимость от частоты ![]() параметра
параметра ![]() для высоких частот (а) и параметра
для высоких частот (а) и параметра ![]() для низких частот (б):
для низких частот (б): ![]() Гц,
Гц, ![]() мм,
мм, ![]() сСт (а);
сСт (а); ![]() Гц,
Гц,
![]() мм,
мм, ![]() сСт
(б).
сСт
(б).
В случае малых
безразмерных частот вибраций толщина слоя Стокса становится сравнимой с
характерными размерами полости. Для характеристики осреднённой скорости
жидкости выберем тот же безразмерный параметр, что и для высокочастотного
случая. экспериментальные
результаты по измерению скорости осредненных течений при малых и умеренных
значениях ![]() , полученные при изменении вязкости
жидкости и параметров вибраций, также вполне удовлетворительно согласуются
между собой на плоскости
, полученные при изменении вязкости
жидкости и параметров вибраций, также вполне удовлетворительно согласуются
между собой на плоскости ![]() (рис. 5б). Характерные значения скорости течения
жидкости в том и другом случае оказываются близкими по порядку величины. Однако
по частоте кривые сдвинуты относительно друг друга на несколько порядков.
(рис. 5б). Характерные значения скорости течения
жидкости в том и другом случае оказываются близкими по порядку величины. Однако
по частоте кривые сдвинуты относительно друг друга на несколько порядков.
Таким
образом, как при низких, так и при высоких значениях безразмерной частоты в
качестве управляющих безразмерных комплексов при описании осредненного течения
жидкости внутри капли могут быть выбраны параметры ![]() и
и
![]() .
.
Заключение. В рамках настоящей работы изготовлена экспериментальная
установка, разработана и апробирована методика, изучены структуры и
интенсивность осредненных потоков изотермической жидкости, возникающих в
осциллирующей капле с упругой границей. Изучено влияние параметров жидкости и
вибраций на закономерности трансформации генерируемых потоков и интенсивность
их течений. Опыты проведены в широком интервале безразмерных частот вибраций.
Выделено три характерных диапазона по частоте: низкие, умеренные и высокие
частоты, для каждого из которых характерна своя картина течений. Показано, что,
помимо безразмерной частоты вибраций ![]() , осредненное
движение жидкости может быть охарактеризовано безразмерным параметром
, осредненное
движение жидкости может быть охарактеризовано безразмерным параметром ![]() .
.
Полученные результаты могут представлять теоретический и практический интерес для занимающихся задачами, связанными с интенсификацией процессов перемешивания жидкости внутри осциллирующей полости, а также вибрационной конвекции жидкости.
Работа выполнена в рамках программы стратегического развития Пермского государственного гуманитарно-педагогического университета (проект 029-Ф) и задания Минобрнауки РФ 2014/372 (проект 2176) при поддержке Министерства образования Пермского края (проект С 26/625).
Рецензенты:Козлов В.Г., д.ф.-м.н., профессор, заведующий кафедрой общей и экспериментальной физики, ФГБОУ ВПО «Пермский государственный гуманитарно-педагогический университет», г. Пермь.
Иванова А.А., д.ф.-м.н., профессор, ведущий научный сотрудник лаборатории вибрационной гидромеханики, ФГБОУ ВПО «Пермский государственный гуманитарно-педагогический университет», г. Пермь.
Библиографическая ссылка
Щипицын В.Д., Вяткин А.А., Козлов Н.В. ЭКСПЕРИМЕНТАЛЬНОЕ ИССЛЕДОВАНИЕ ТЕЧЕНИЯ В ОСЦИЛЛИРУЮЩЕЙ КАПЛЕ С УПРУГОЙ ГРАНИЦЕЙ // Современные проблемы науки и образования. 2014. № 6. ;URL: https://science-education.ru/ru/article/view?id=16613 (дата обращения: 05.07.2025).



