Получить специальные знания в соответствующих областях техники и технологии, сформировать определенную культуру научного мышления можно только на добротной основе естественнонаучного образования, фундаментом которого являются физика и химия. При этом основным компонентом процесса обучения выступает решение задач, что позволяет: понять и запомнить основные законы и формулы, сформировать представление об их характерных особенностях и границах применения; развивать умения и навыки использования общих законов для решения конкретных, практических вопросов.
Анализ использования задач при изучении естественнонаучных дисциплин позволяет выделить их основные функции:
- познавательная, позволяющая расширить кругозор обучающихся, используя данные о жизни и деятельности учёных, интересные факты, связанные с физическими явлениями и химическими объектами;
- развивающая, состоящая в совершенствовании умений работать с разными видами представления информации (таблицами, рисунками и т.д.), а также развитии логического мышления, поскольку при решении задач используются такие логические операции, как анализ, синтез, сравнение, абстрагирование и обобщение;
- функция единства теории и практики, выражающаяся в формировании умений использовать законы физики и химии для решения практических задач в профессиональной деятельности, а также в быту;
- функция демонстрации междисциплинарных связей физики, химии, математики, дисциплин профессионального цикла;
- функция оценки качества знаний обучающихся. Правильность решения задачи позволяет объективно отразить уровень усвоения учебного материала, проверить, насколько качественно он усвоен. Приведённые функции показывают, насколько важен процесс решения задач в изучении естественнонаучных дисциплин.
На наш взгляд, обучение, как школьников, так и студентов решению задач по физике и химии должно быть выстроено на основе деятельностного подхода. Как отмечает Г.А. Атанов, именно этот подход, основанный на «… решении задач, … позволяет наглядно и эффективно организовать деятельность обучаемых» [1]. Разработанная для учащихся старших классов, слушателей подготовительных курсов методика обучения решению задач по физике на основе деятельностного подхода успешно используется и для студентов, и главное – позволяет получать высокие результаты обучения [3]. Данная методика содержит следующие этапы: 1) подготовительный, 2) разработки алгоритма для задач данного типа, 3) диагностики и обучения несформированным действиям, 4) решения задач, 5) контрольно-рефлексивный [3].
В ходе проведённых исследований проектирование учебной деятельности строилось на основе диагностики испытываемых обучающимися трудностей в процессе решения задач при выполнении ими отдельных действий и операций. При этом были сделаны выводы о том, что обучающиеся более успешно решают задачи при наличии развёрнутой операционной основы деятельности по их решению, а также при выделении и формулировании подцелей в ходе решения с опорой на «ключевые признаки» в структуре рассматриваемой задачи.
Одной из основных целей деятельности по решению, в частности физических задач, является выработка алгоритмических предписаний к решению задач по конкретным темам с последующим обобщением и систематизацией полученного опыта – получением детализированного плана решения произвольной физической задачи, который систематизирован и представлен в виде схемы (рис.1).
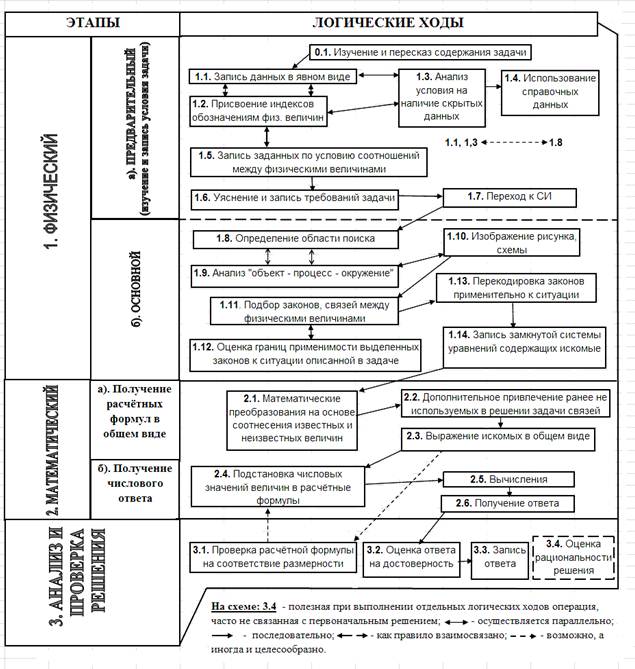
Рис.1. Детализированный, обобщённый план решения
произвольной физической задачи (авторская схема)
При этом в процессе решения задач определённого вида помимо выявления особенностей их решения и отработки конкретных операций по их решению осуществляется свёртывание их в обобщённые действия. Раскрытие содержания общих способов действий, направленных на решения задач, чрезвычайно важно, поскольку именно на освоение общих способов действий и должна быть направлена учебная деятельность обучающихся. Опираясь на ключевые признаки, обучающиеся объясняют цель и содержание каждого шага в решении, что в итоге приводит к свободной ориентации в структуре задачи. Так, например, при рассмотрении задачи 1 (рис.2) обучающиеся выделяют – «математические преобразования», «уяснение и запись требований задачи». В задаче 2 – «анализ на наличие скрытых данных», «использование справочных данных» (поскольку в задаче рассматривается движение точки земной поверхности, то можно и нужно записать радиус Земли, кроме того, её период обращения – 24 ч). В задаче 3 – «изображение рисунка», анализ «объект – процесс – окружение». При обсуждении второго выделенного логического этапа рассматриваются методы упрощения и усложнения. Так, в процессе упрощения используются идеализация, оценка и отбрасывание второстепенных явлений, пренебрежение несущественными деталями, в процессе усложнения – учёт и рассмотрение ранее отброшенных деталей, объектов, явлений. Решая эту задачу, вводим упрощающее условие – сопротивлением воздуха пренебречь. Убрав это условие, мы усложняем задачу. Траектория будет отличаться от параболы и движение по отношению к оси x уже не будет равномерным. Кроме того, считаем, что: а) тело брошено с поверхности Земли; б) тело можно принять за материальную точку; в) не учитываем движение Земли вокруг Солнца и вокруг собственной оси; г) считаем ускорение свободного падения ![]() и т. д. Учитывая любое из приведенных упрощений, мы усложняем задачу.
и т. д. Учитывая любое из приведенных упрощений, мы усложняем задачу.
|
1. Точка движется в плоскости XОY, и при этом её координаты изменяются с течением времени по закону:
2. Найти линейную скорость вращения точек земной поверхности на широте
3. Тело брошено под углом α к горизонту с начальной скоростью |
Рис. 2. Условия физических задач
Анализ – логический приём, состоящий в том, что изучаемый объект (в нашем случае учебная задача) мысленно расчленяется на составные элементы (признаки, свойства, отношения), каждый из которых исследуется в отдельности как часть расчленённого целого. Синтез – логический приём, с помощью которого отдельные элементы соединяются в целое. Умение мыслить очень часто связывают с умением анализировать. Это вполне справедливо, так как вывод следствий, выражающих новые свойства изучаемого объекта, очень часто требует анализа того, что уже известно о нём. Особое значение навыков и умений осуществлять анализ на каждом из выделенных этапов решения задачи наглядно отражает детализированный план решения произвольной физической задачи. Уже на предварительном, физическом этапе самый первый шаг – «Изучение и пересказ содержания задачи» (именно пересказ, то есть целостное воспроизведение условия и требований задачи, а не дословное воспроизведение) – опирается на умения и навыки осуществлять анализ. Неспособность ученика целостно воспроизвести содержание задачи говорит о том, что задача им не принята и к её непосредственному решению приступать нельзя.
Конечно, при решении задач трудно выделить в чистом виде анализ или синтез, они взаимосвязаны. Поэтому часто говорят об аналитико-синтетическом методе решения. Тем не менее, «… когда решение выстраивают исходя из вопроса (требований) задачи, на передний план выступает все же анализ» [2]. Подбор определённой системы задач и их рассмотрение с акцентом на содержание деятельности по их решению, позволяет выработать рекомендацию об обязательной попытке построить решение исходя из вопроса или требований задачи. Эта рекомендация позволяет снять одну из существенных трудностей обучающихся, состоящую в том, что многие из них часто просто не знают и не понимают, с чего начать решение задачи.
Большинство стандартных задач можно решить аналитическим методом, выстроив решение исходя из вопроса (требований) задачи, однако не все. Когда так выстроить решение нельзя, используется синтетический метод, и на передний план выступает синтез, так как синтезируются различные соотношения, которые могут быть установлены по данным и условию задачи. Таким образом, целесообразно начинать решение вычислительной задачи либо с вопроса задачи, либо с основного закона (законов), описывающего физическое явление (явления), рассматриваемое в данной задаче. В целом, независимо от выбора метода (аналитического или синтетического), успех в решении задачи определяется умением провести анализ физической ситуации, описанной в задаче, в основе которого лежит умение выделить главное.
В таблице 1 приведена система основных приёмов, использующихся для развития умений обучающихся осуществлять анализ в процессе решения задач, которая условно разделена на две группы. Первая группа связана с действиями преподавателя и обучающихся в процессе обсуждения и решения задачи, вторая – с переконструированием исходного содержания задачи.
Таблица 1
Система приёмов по развитию умений осуществлять анализ в процессе решения задач
|
Группа приёмов |
Название приёма |
Основные идеи и принципы приёма |
|
1 |
1.1. Пошаговое объяснение каждого этапа решения задачи |
Формулировка вслух целей и содержания каждого шага в решении задачи. Особое внимание уделяется – анализу физической ситуации описанной в задаче |
|
1.2. Поиск аналогии |
Поиск подобия в содержании, последовательности и способах действий в решении с рассмотренными ранее задачами |
|
|
1.3. Создание проблемной ситуации с помощью «случайной» ошибки |
Преподаватель целенаправленно допускает ошибку, приводящую к абсурдному результату; «не замечает» допущенной ошибки ученика |
|
|
1.4. Оценка рациональности решения |
Попытка решения разными способами, поиск наиболее оптимального |
|
|
2 |
2.1. Исключение «лишних» данных из условия и требований задачи |
Из текста задачи исключаются заданные в готовом виде обозначения величин, соотношения между ними (р = ; L1 = 1,5 L2), содержащиеся справочные данные и так далее |
|
2.2. Преобразование к задаче с недостающими или избыточными данными |
Введение в условие задачи излишних данных и наоборот исключение необходимых |
|
|
2.3. Упрощение (усложнение) ситуации описанной в задаче |
Идеализация, оценка и отбрасывание второстепенных явлений, пренебрежение несущественными деталями (учёт и рассмотрение ранее отброшенных деталей, объектов, явлений) |
|
|
2.4. Вариативность в способах представления содержания задачи |
Переход от текстового описания условия к условию заданному таблицей, графиком, диаграммой и наоборот |
По сравнению с физикой в химических задачах используется гораздо меньше величин, необходимых для решения. Тем не менее, вышеизложенная методика обучения решению задач на основе деятельностного подхода может быть успешно использована в преподавании химии. В обобщённом плане решения произвольной задачи вместо физического выделяется химический этап, в котором вещества и их превращения рассматриваются с качественной стороны. Одним из наиболее важных этапов при решении химической задачи, ведущим к пониманию её смысла, мы считаем предварительный анализ текста, предполагающий уточнение отдельных терминов, перефразирование и переформулирование условия, в результате чего выясняется, о химическом процессе или о конкретном веществе говорится в условии задачи.
К применяемым нами методическим приёмам, способствующим развитию умений осуществлять анализ в процессе решения химических задач, относятся:
· сравнение. Приводятся условия двух задач (например, 1) рассчитать массу хлорида алюминия, необходимую для приготовления 2 л раствора с молярной концентрацией растворённого вещества 2 моль/дм3; 2) рассчитать массу хлорида алюминия, необходимую для приготовления 2 л раствора с молярной концентрацией эквивалента растворённого вещества 2 моль/дм3), сравнивая которые, студент обучается выделять признаки и свойства у объектов, устанавливать сходство и различие между признаками, выделять основания для сравнения;
· выбор (правильного ответа / расчётной формулы для решения задачи), способствующий усвоению структуры задачи, установлению взаимосвязи между данными и искомыми величинами, обоснованию своих суждений;
· конструирование (например, какими данными нужно дополнить условие задачи), при использовании которого студент переносит усвоенные знания на область новых знаний, включается в активную поисковую деятельность, структурируя данные, анализируя и преобразуя математическую модель задачи;
· схематическое моделирование задачи, позволяющее перевести текст на знаково-символический язык, который может осуществляться вещественными или графическими средствами, тем самым увеличивая доступность для понимания связей и отношений, скрытых в тексте, а также соотнести результаты, полученные на модели, с реальностью (с текстами).
Иногда перевод текста на знаково-символический язык химических формул и уравнений реакций делает настолько явными зависимости между величинами, фигурирующими в задаче, что сразу же способствует нахождению решения. В процессе построения модели нами используется подход Ж. Вернье [4], в котором используются категории состояния объекта, описанного в тексте задачи и его трансформаций. При этом данные изображаются в виде геометрических фигур, а отношения между объектами – в виде линий и стрелок. Использование одних и тех же знаково-символических средств при построении модели для задач разного типа способствует формированию общих способов действий в процессе анализа задачи, выделению составляющих ее компонентов и нахождению путей решения.
Динамика развития умений осуществлять анализ в процессе решения задач по физике и химии регулярно диагностировалось с помощью специально разработанных заданий и системы задач [5, 6]. Результаты проведённых исследований позволяют утверждать [3], что обучение студентов общим приемам умственной деятельности, а в частности, анализу, является наиболее эффективным при организации обучения решению задач.
Рецензенты:
Сапожков С.Б., д.т.н., проф. заведующий кафедрой естественнонаучного образования Юргинского технологического института Томского политехнического университета, г.Томск;
Соколова И.Ю., д.п.н., профессор кафедры инженерной педагогики Национального исследовательского Томского политехнического университета, г.Томск.
Библиографическая ссылка
Полицинский Е.В., Деменкова Л.Г. РАЗВИТИЕ УМЕНИЙ ОБУЧАЮЩИХСЯ ОСУЩЕСТВЛЯТЬ АНАЛИЗ В ПРОЦЕССЕ РЕШЕНИЯ ЗАДАЧ // Современные проблемы науки и образования. 2014. № 6. ;URL: https://science-education.ru/ru/article/view?id=16592 (дата обращения: 03.04.2025).



