Концепция построения дискретного электропривода (ДЭП) с шаговым двигателем (ШД) в робототехнических комплексах направлена на упрощение структуры привода, повышение его гибкости, унификации в программном и аппаратном обеспечении, на полный или частичный отказ от стандартных датчиков положения, в частности, с реализацией контроля путевой координаты на основе косвенной информации. Такая информация может быть получена в результате обработки сигнала штатного пьезоэлектрического датчика ДЭП – акселерометра, который используется в контуре локальной обратной связи для демпфирования колебаний якоря (ротора) ШД. Система организуется как поисковая с экстремальным регулированием момента (усилия – для линейных двигателей). Преследуется цель достижения ортогонального положения электрической и механической осей шагового двигателя и программной коррекции известной величины динамической ошибки. Однако достижение устойчивой работы такого привода требует глубокого синтеза структуры и определения целого комплекса условий, в частности, связанных с ограничениями со стороны инвертора тока.
Синтез структурной схемы дискретного электропривода
Задача повышения статических и динамических качеств дискретного электропривода с шаговым двигателем в замкнутой структуре с косвенным контролем путевой координаты, определяет необходимость применения методов исследования системы с учетом ее импульсного характера по управлению и питания обмоток шагового двигателя от управляемого инвертора тока, сохраняющего свои свойства в ограниченном частотном диапазоне. Синтез электропривода целесообразно осуществить, используя математическое описание в преобразованных координатах d, q, связанных с подвижным элементом двигателя.
Система уравнений, представляющая процессы в разомкнутом приводе в дифференциальной форме, имеет вид [1]
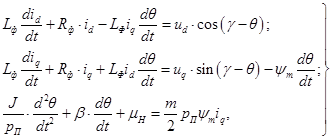(1)
где Rф - сопротивление обмотки ШД: Lф - индуктивность обмотки; id и iq - мгновенные токи в ортогональных фазах по осям d и q; ψт - потокосцепление; J - момент инерции; μН - момент сопротивления нагрузки; pП - число пар полюсов; ud, uq - напряжения фаз по осям; θ - угол поворота ротора ШД; γ - управляющее воздействие; β - коэффициент вязкого трения.
Для привода, работающего в режиме квазизамкнутого режима, система уравнений (1) при условиях:
id =0; 
= 0; 
=1,
будет иметь вид
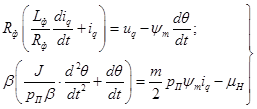(2)
Введя обозначения: ТЭ = LФ/RФ; ТМ = J/( pП β); кД = 
; 
; 
; 
=
и применив преобразование по Лапласу, получим систему вида
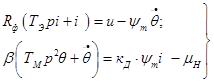(3)
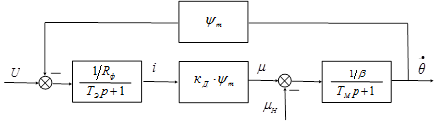
Система дифференциальных уравнений (3) соответствует структурной схеме (рис. 1а).
а)
б)
в)
Рис.1. Структурные схемы дискретного электропривода
Передаточная функция этой системы по управлению для выходной координаты 
в операторной форме имеет вид
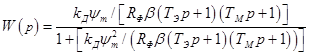
или
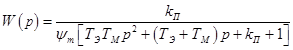, (4)
где 
– безразмерный коэффициент, определяемый параметрами привода.
Передаточная функция системы по нагрузке 
при выходной переменной имеет вид
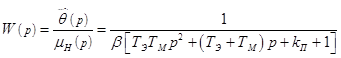. (5)
При питании обмоток ШД от инвертора тока обеспечивается компенсация ЭДС движения и, следовательно, отрицательной обратной связи по скорости. Результатом этого является существенное снижение постоянной времени ТЭ. В этом случае ТЭ = 0, 
= 0 система уравнений (2) трансформируется в выражение
(6)
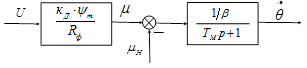
которому соответствует структурная схема, показанная на рисунке 1б.
Передаточные функции инвертора тока 
по управлению и нагрузке соответственно [2]
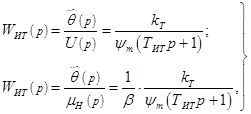(7)
где 
, 
– коэффициент передачи и постоянная времени инвертора тока.
Включение в структуру привода измерителя динамической ошибки позволяет осуществить контроль за рассогласованием по положению ΔUѲ = (ѲПР – Ѳ)h, где h – коэффициент преобразования, соответствующий величине сдвига щеток от нейтрали в бесконтактном двигателе постоянного тока [4].
Оптимизация привода по критериям качества требует выбора типа регулятора. В дискретном электроприводе в структуре с инвертором тока это может быть достигнуто при использовании ПИ-регулятора [3]. Передаточная функция по управлению будет иметь вид
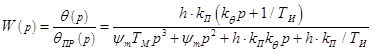. (8)
Условия оптимизации могут быть представлены системой уравнений
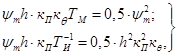(9)
в соответствии с которыми параметры регулятора:
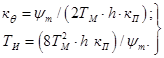(10)
Практическая реализация ПИ-регулятора может быть реализована как на аппаратном уровне, так и программными средствами и в общем виде представляется известным образом:
. (11)
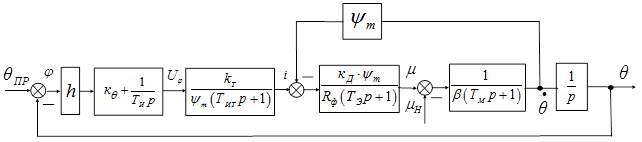
Таким образом, замкнутому электроприводу соответствует структурная схема на рис.1в.
Исследования дискретного электропривода
Экспериментальные исследования дискретного электропривода проводились с шаговым двигателем типа ДШИ-200-2. Основные технические характеристики привода: m = 2; RФ = 3,12 Ом; ТЭ = 0.43·10-3 с; ТМ = 38·10-3 с; ММАХ = 0.5 Н·м; 
= 4,5 мВ/эл.рад.с-1; 
= 10-5 Нм·с; 
= 1,22; 
= 0,63 В/эл.рад.; 
= 1,24; ТИ = 2,5 мс.
Устойчивая работа рассматриваемой системы в значительной степени зависит от характеристик управляемого инвертора тока, который генерирует приводу свойства источника момента (усилия – для линейных ШД). ДЭП сохраняет таковые в области работы до ограничительной механической характеристики 
(рис. 2, кривая 1), подчиняющейся закону [1]
,
где ϰ – ЭДС в о. е.; δ – безразмерный коэффициент внутреннего и внешнего вязкого трения; 
– напряжение питания инвертора тока.
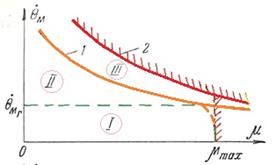
Рис. 2. Граничные механические характеристики ДЭП
Исследования показывают, что в области вблизи ограничительной механической характеристики привода начинает проявляться колебательность процессов 
, 
(рис. 3а, 
– задание 
).
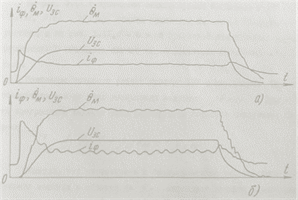
Рис. 3. Осциллограммы , UЗС, iФ в функции времени
Работа привода выше ограничительной механической зависимости характеризуется снижением динамического коэффициента передачи инвертора 
и вызывает значительные отклонения регулируемого параметра 
от заданного 
. Это связано с тем, что для данного значения 
в пространстве состояний существует такое граничное значение 
, при превышении которого за счет компенсации ЭДС вращения напряжения питания инвертора искажаются формируемые программными средствами кривые токов в фазах ШД. В результате появляется дополнительный фазовый сдвиг между током фазы и ЭДС ортогональной фазы, не соответствующий значению φ=π/2 (рис. 4). Ортогональность электрической и механической осей шагового двигателя нарушается. Динамическая ошибка привода уже не равна заявленной программной величине.
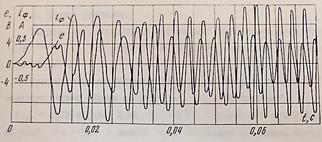
Рис. 4 . Осциллограммы , еФ, iФ в функции времени в области выше
Степень колебательности процессов возрастает (см. осциллограммы на рис. 3б), хотя при детерминированной величине устойчивость привода существенно не нарушается, – возрастает лишь ошибка воспроизведения движения [5]. Основным условием работы в области 3 (рис. 2) – с постоянной мощностью Р = const – является ограничение величины нагрузки , которую необходимо снижать при увеличении частоты вращения оси ШД.
Экспериментами и моделированием показано [6], что для снижения времени установления требуемого значения динамической ошибки в нестационарных режимах работы привода необходимо при пуске осуществлять программный сдвиг поля ШД на угол
. На рисунке 5 продемонстрированы осциллограммы переходных процессов пуска , еФ, iФ в функции времени с программным изменением скорости по экспоненциальному закону до значения = 40 с-1.
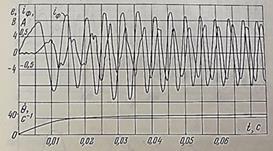
Рис. 5. Осциллограммы , еФ, iФ в функции времени в области до
Ортогональная ориентация электрической и механической осей шагового двигателя после завершения переходных процессов (время переходного процесса tПП = 0,07 с) соответствует норме, о чем свидетельствует фазовый сдвиг между током фазы iФ и ЭДС ортогональной фазы еФ φ = π/2.
Заключение
Управление с косвенным замыканием путевой координаты устраняет основной недостаток разомкнутого ДЭП – влияние нагрузки на величину динамической ошибки и точность воспроизведения движения.
Эмпирическая методика исследований доказательно показывает возможность воспроизведения траекторных перемещений в установившемся режиме с ошибкой, не зависящей от изменяющейся величины нагрузки при условии сохранения источником тока заданных свойств.
Рецензенты:
Присмотров Н.И., д.т.н., профессор ФГБОУ ВПО «Вятский государственный университет», г. Киров;
Хорошавин В.С., д.т.н., профессор ФГБОУ ВПО «Вятский государственный университет», г. Киров.
Библиографическая ссылка
Лалетин В.И., Сбоев В.М., Рычков В.В. СИНТЕЗ ДИСКРЕТНОГО ЭЛЕКТРОПРИВОДА С КОСВЕННЫМ ЗАМЫКАНИЕМ ПУТЕВОЙ КООРДИНАТЫ // Современные проблемы науки и образования. – 2014. – № 6. ;URL: https://science-education.ru/ru/article/view?id=16332 (дата обращения: 23.04.2024).