Для случая обработки токарными резцами с вершиной при её острой и закругленной форме параметры действительного и остаточного сечения детально рассмотрены в работах Г.И. Грановского и его последователей. Однако для наружного продольного точения безвершинными резцами принципиальным отличием от обработки традиционными резцами служит отсутствие вершины. Вместо нее в процессе формообразования участвует протяженная режущая кромка (рисунок 1). При этом в значительной степени меняются условия резания, выражающиеся в изменении геометрии лезвия и формирования сечения срезаемого слоя.
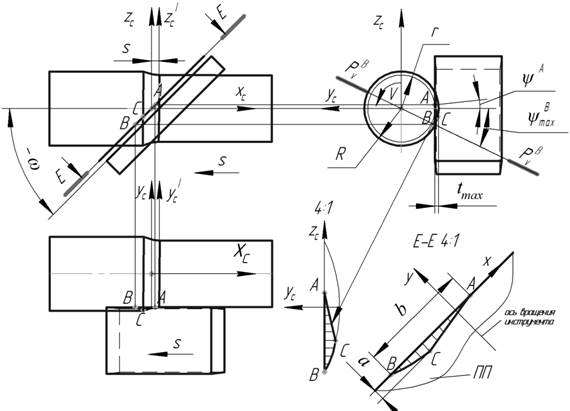
Рисунок 1 – Схема процесса косоугольного точения безвершинным резцом с прямолинейной режущей кромкой и параметры сечения срезаемого слоя (ПП – передняя поверхность инструмента)[7]
В связи с этим для приближенного теоретического нахождения шероховатости поверхности по параметру Rz можно воспользоваться кинематико-геометрическим методом. В основу, которого положено нахождение высоты остаточного сечения, значение которой принимается приближенно равным параметру Rz.
Основные результаты
Вопросу теоретического нахождения высоты остаточного сечения и шероховатости обработанной поверхности при точении безвершинными резцами с прямолинейной режущей кромкой посвящены работы Г.С. Минасяна [1] и W. Grzesik[8]. В своих работах они предлагают различные схемы и формулы для нахождения высоты остаточного сечения. В этой связи рассмотрим представленные ими данные.
Для расчетного определения высоты микронеровностей при точении безвершинным резцом БРМ-1 в работе [1] приводится схема, основанная на том, что поверхность резания является однополостным гиперболоидом вращения (рисунок 2). С учетом того, что значения высоты остаточного сечения (h) значительно меньше диаметра обрабатываемого изделия (d) автор [1] предлагает для нахождения величин (h) использовать приблизительную формулу:
(1)
где s – подача;
– угол наклона передней грани.
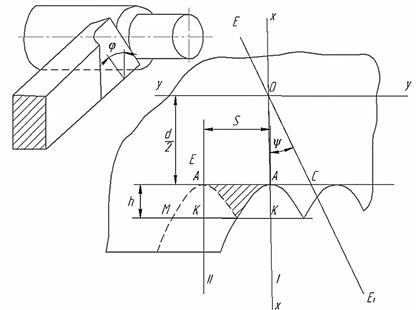
Рисунок 2– Схема для расчетного определения высоты остаточного сечения по данным
Г.С. Минасяна [1]
Формула (1) хоть и является приближенной, однако дает возможность на качественном уровне оценивать влияние кинематико-геометрических особенностей процесса (подачи, диаметра обрабатываемой поверхности и угла наклона лезвия) на параметр шероховатости Rz.
Основываясь на аналогичном положении (что поверхность резания является гиперболоидом вращения) автор работы [8] для теоретического нахождения величин высоты неровностей профиля (Rz), предлагает использовать уравнение:
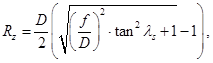(2)
где f – подача;
D – диаметр заготовки;
λs – угол наклона режущей кромки.
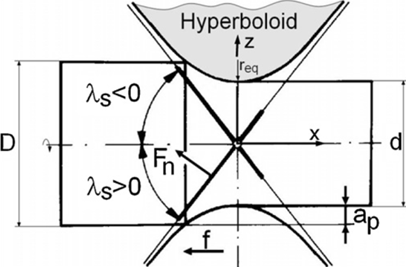
Рисунок 3 –Схема процесса точения безвершинным резцом по данным WitGrzesik [2]
Как показано в работах [5-7, 10], при косоугольном точении безвершинным резцом с прямолинейной режущей кромкой, обрабатываемая поверхность представляет собой поверхность однополостного гиперболоида вращения, сечением которого в горизонтальной и вертикальной плоскости является гипербола (3).
(3)
где
– параметры гиперболы, определённые из
условия, что проекция РК на плоскость ZOX является её асимптотой;
r – радиус обработанной поверхности;
ω – угол наклона лезвия (см. рисунок 1).
С точки зрениягеометрии при перемещении инструмента в направлении подачи за один оборот заготовки образуются две гиперболы, пересекающиеся в общей точке A (рисунок 4). Эти гиперболы образуют собой остаточное поперечное сечение ограниченное контуром ABC.
В работе [1] приводится приближенная формула для определения высоты (Н), она имеет погрешность при больших значениях угла наклона лезвия и при больших подачах. В связи с этим была составлена более точная формула (4), в основе которой лежит определение точки пересечения двух гипербол образованных при перемещении инструмента на величину подачи (см. рисунок 4).
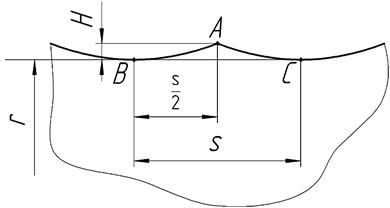
Рисунок 4 –Схема определения высоты остаточного сечения
Высота остаточного сечения (гребешка)
зависит от подачи (s), угла наклона лезвия (w)
и глубины резания (t), которая выражается через радиус
обработанной поверхности 
. Таким
образом, с учетом формулы (3), максимальную высоту поперечного остаточного
сечения определим по формуле:
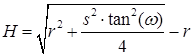(4)
На рисунке 5 представлены зависимости изменения максимальной высоты остаточного сечения от угла наклона лезвия и подачи для разных значений глубины резания. Как видно из представленных зависимостей, увеличение подачи и угла наклона лезвия приводит к значительному увеличению высоты (H), в то время как увеличение глубины резания приводит к незначительному увеличению H. Это является важным обстоятельством, поскольку правильный выбор режимов обработки и параметров установки инструмента будет определять качество обработанной поверхности.
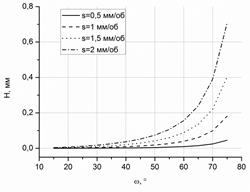
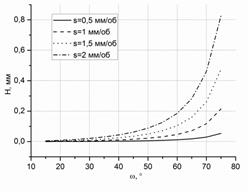
а) б)
Рисунок 5 – Зависимость изменения высоты остаточного сечения от угла наклона лезвия и подачи: R=10мм, глубина резания а) t=0,5 мм; б) t=2мм.
На рисунке 6 представлены результаты расчета высоты остаточного сечения срезаемого слоя материала по формулам Г.С. Минасяна (1), W. Grzesik(2) и формуле автора (4).полученной на основе данных работ [4-7, 9].
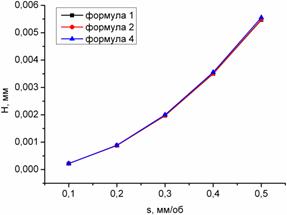
Рисунок 6 – Зависимость высоты остаточного сечения от подачи
Выводы
На основе рассмотренных и полученных данных можно сделать следующие выводы:
1. В результате сопоставления расчетных формул Г.С. Минасяна (1), W. Grzesik(2) и предложенной автором (4) установлено незначительное отклонение результата определения высоты остаточного сечения. Следовательно, все эти формулы могут быть использованы для приближенной оценки высотного параметра шероховатости поверхности Rz.
2. Несмотря на возможность приближенного расчета Rzпо высоте остаточного сечения с использованием кинематико-геометрического метода невозможно точно рассчитать величину шероховатости обработанной поверхности, поскольку при обработке резанием в зоне стружкообразования протекают сложные деформационные процессы [3], которые также участвуют в формировании поверхностного слоя детали и влияют на шероховатость поверхности.
Рецензенты:
Сапожков С.Б., д.т.н., заведующий кафедрой естественно-научного образования ФГБОУ ВПО «Юргинский технологический институт (филиал) Национального исследовательского Томского политехнического университета», г. Юрга.
Петрушин С.И., д.т.н., профессор кафедры технологии машиностроения ФГБОУ ВПО «Юргинский технологический институт (филиал) Национального исследовательского Томского политехнического университета», г. Юрга.
Библиографическая ссылка
Филиппова Е.О. ТЕОРЕТИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЫСОТЫ ОСТАТОЧНОГО СЕЧЕНИЯ ПРИ КОСОУГОЛЬНОМ ТОЧЕНИИ БЕЗВЕРШИННЫМ РЕЗЦОМ // Современные проблемы науки и образования. – 2014. – № 6. ;URL: https://science-education.ru/ru/article/view?id=16188 (дата обращения: 19.04.2024).