Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Кацман Ю.Я. 1 Лепустин А.В. 1 Илюхин Б.В. 2

---

1 ФГАОУ ВПО «Национальный исследовательский Томский политехнический университет»

2 ФГБОУ ВПО «Томский государственный университет систем управления и радиоэлектроники»

В данной статье исследованы оценки эффективности работы школ Томской области в зависимости от типа населенного пункта (областной центр, небольшой город, село, малокомплектные школы). Обработка экспериментальных данных проводился в программе STATISTICA. С помощью критериев Стьюдента и Фишера сравнивались образовательные результаты различных типов школ. С помощью линейного корреляционного анализа были выявлены наиболее существенные переменные (контекстные факторы), влияющие на результаты ЕГЭ школьников по русскому языку и математике. На следующем этапе были построены многомерные линейные регрессионные модели для различных оценок и типов школ. В работе подробно рассматривалось качество моделей, обсуждалось качество коэффициентов уравнения регрессии. С учетом неоднозначного влияния различных факторов (переменных) на оценки эффективности работы разных типов школ, определялась оптимальная размерность модели. На основании полученных результатов сделаны выводы о применимости многомерных линейных моделей для оценки образовательных достижений учеников.

Статья в формате PDF

229 KB

оценка

статистика

критерий

корреляция

регрессия

переменная

контекстный фактор

гипотеза

модель

среднее значение

дисперсия

диаграмма рассеяния

доверительный интервал

коэффициент детерминации.

1. Болотов В.А., Вальдман И.А. Информирование различных целевых групп как условие эффективного использования результатов оценки учебных достижения школьников. // Проблемы современного образования. – 2012. – № 6. – С. 187-202. [Электронный ресурс]. – Режим доступа: http://www.pmedu.ru/res/2012_6_13.pdf (дата обращения 10.11.14).

2. Болотов В.А., Вальдман И.А., Ковалёва Г.С., Пинская М.А.. Анализ опыта создания российской системы оценки качества образования. // Управление образованием: теория и практика. Вып. 1-2, 2011. URL: http://www.iuorao.ru/2010-01-01-14 (дата обращения 10.11.14).

3. Боровиков В. STATISTICA. Искусство анализа данных на компьютере: Для профессионалов. 2-е изд. (+CD).  СПб.: Питер, 2003.  688 с.

4. Горлов П.И., Илюхин Б.В., Возможность использования ресурсов Центра оценки качества образования Томской области для создания элементов региональной системы оценки качества образования. //Качество образования в Евразии. – 2013. – №1, С. 123-135.

5. Илюхин Б.В., Оценка качества образования и принцип разумной достаточности. //Народное образование. – 2012. – №6. С. 118-126.

6. Индикаторы оценки качества образования / М.Л. Агранович, П. Кондрашов // Директор школы. – 2007. – № 5. – С. 5-16. – (Образовательная политика)

7. Кашпур В.В., Рачилина М.В., Илюхин Б.В. Фоновые факторы, влияющие на результаты ЕГЭ. – Томск, Дельтаплан, 2008. 100 с.

8. Сербина Н.П., Кацман Ю.Я., Илюхин Б.В. Результаты мониторинга качества образования в образовательных учреждениях системы общего образования Томской области. Томская область – Томск; Дельтаплан, 214, 80 с. – URL: http://coko.tomsk.ru/files/reports/itog-monit-2014.pdf (дата обращения 02.12.2014).

9. Центр оценки качества образования томской области. Программа InfoCollector (Паспорт школы) 2.0. URL: http://coko.tomsk.ru/files/infomonitoring/InfoCollector.pdf (дата обращения 02.12.2014).

10. Школы, эффективно работающие в сложных социальных контекстах / М.А. Пинская, С.Г. Косарецкий, И.Д. Фрумин //Вопросы образования – 2011. №4 – С. 148-177.

Официальных критериев оценки эффективности образовательной организации, на сегодняшний день не существует. Очевидна невозможность применения бизнес-критериев (в том числе финансовых). Иными будут и предметы оценки. В рамках концепции Общероссийской системы оценки качества образования (2008) выделяются три объекта оценки: ресурсы, образовательные программы и образовательные результаты (как указано в Концепции – наиболее важный объект оценки). При этом, необходимо учитывать, что набор стандартизованных инструментов для получения объективной оценки учебных достижений крайне невелик как в Российской Федерации, так и в мире.

Наиболее стандартизованной процедурой оценки качества образования в России сегодня является Единый государственный экзамен (ЕГЭ). Изначально он вводился как инструмент стратификации выпускников и абитуриентов. К сожалению, в последнее время, ЕГЭ использовался органами управления образованием различных уровней как основной инструмент оценки эффективности работы школ, и соответственно, один из значимых критериев распределения средств. Однако образование не является замкнутой и закрытой системой, и на его результаты оказывают значительное влияние так называемые «контекстные факторы» [1] ‑ уровень социально-экономического развития территории, образовательный ценз родителей и пр.

Исследования [7] показали существенную зависимость результатов школьников от отношения к ЕГЭ администрации школ и учителей, квалификации и уровня образования педагогов, и ряда других факторов. На качество образования влияют и экономические факторы [6], а результаты исследования [10] показывают, что отдельные школы могут быть эффективны даже в сложных социальных контекстах. Подобные выводы содержатся и в работах, описывающих российский и международный опыт [2, 10]. Авторами была предпринята попытка уточнить с учетом региональной специфики перечень ключевых контекстных факторов, оказывающих наиболее значимое влияние на образовательные результаты школьников, оценить степень их влияния. Финансовые, социальные и иные показатели школ и контингента обучающихся были собраны в рамках формирования социальных паспортов образовательных организаций (ОО), как элемента построения региональной системы оценки качества образования [4 – 5, 8]. В результате была собрана информация по 188 параметрам, характеризующая каждую из 229 образовательных организаций Томской области, реализующих программы полного среднего общего образования в 2011-2012 учебном году. С полным перечнем собираемых данных, можно ознакомиться на сайте [9]. Для проведения исследования результатов ЕГЭ выпускников школ Томской области была использована методика, описанная в работе [7].

Цель и задачи исследования

Основной целью исследования является выявление отдельных факторов, наиболее существенно влияющих на образовательные результаты, а также совершенствование методов корректного сопоставления различных школ [7].

В работе были решены следующие задачи:

‑ сравнение образовательных результатов отдельных школ, расположенных в различных типах населенных пунктов (крупных городов, сел, малых сел, и пр.);

‑ влияния групп факторов [1, 7] на образовательные результаты школьников;

‑ эффективность методики [7] оценки влияния различных факторов на образовательные результаты школьников;

‑ построение линейной многомерной регрессионной модели, описывающей эффективность образовательных результатов школ, в зависимости от количества регрессоров; оценка качества модели.

Результаты исследований

В качестве оценки эффективности работы школ изначально были рассмотрены результаты сдачи ЕГЭ: средний балл (русский язык) и средний балл (математика).

Все исходные данные были сведены в единую таблицу, содержащую 229 строк (школы) и 183 столбца (переменные). Обработка данных проводилась в пакете STATISTICA.

А. Сравнение оценок для школ различных типов ОО

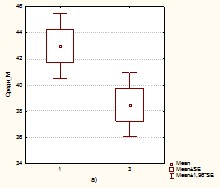
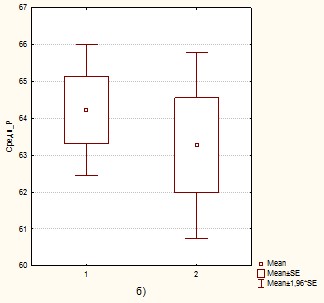
В исследовании предполагалось, что для выпускников различных ОО могут наблюдаться значимые различия в оценках эффективности. С этой целью все школы области были разбиты на 4 не пересекающиеся группы: 1 – школы г. Томска; 2 – городские школы (городское население < 100 000); 3 – малокомплектные школы; 4 – сельские и поселковые школы. Результаты оценок, полученных для разных типов школ, представлены на рис. 1.

Рис. 1. Результаты ЕГЭ для различных ОО Томской области.

Представленные диаграммы размаха показывают, что для оценок по разных предметам и различных типов ОО наблюдается как существенное отличие средних и практически не перекрывающиеся доверительные интервалы (рис. 1а), так и практическое равенство средних и совпадение доверительных интервалов (рис. 1б). Анализ результатов свидетельствует о том, что для различных ОО максимальное отличие оценок ЕГЭ по русскому языку составляет ~ 6 баллов, для оценок по математике это разница – менее 4,5 баллов. Об отличии средних оценок свидетельствуют и не перекрывающиеся (частично перекрывающиеся) доверительные интервалы, которые рассчитывались при доверительной вероятности равной 95%.

С точки зрения математической статистики задачу равенства / не равенства средних значений двух выборок можно решить, например, с помощью критерия Стьюдента: проверяем гипотезу против гипотезы при заданном уровне значимости α = 0,05. Применение критерия Стьюдента ограничено условиями: выборки (переменные) должны иметь гауссово распределение и их дисперсии должны быть равными.

Проверка нормальности распределения проводилась в пакете SATISTICA для двух оценок и всех типов ОО при уровне значимости α = 0,05. Типичный результат исследования представлен на рис. 2.

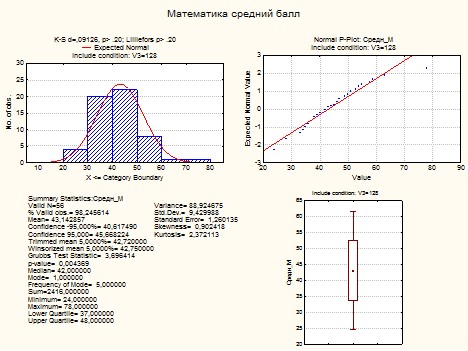
Рис. 2. Проверка нормальности распределения оценок ОО г. Томска

В верхнем ряду рис. 2 слева приведена гистограмма частот переменной Средн_М. Здесь же представлено гауссово распределения с параметрами равными экспериментальным данным. Сверху гистограммы приведены результаты проверки критериев Колмогорова-Смирнова и Лиллефоса. Так как вероятность принятия нулевой гипотезы значительно больше уровня значимости, делаем вывод о нормальном распределении переменной. Данный результат наглядно подтверждается графиком на нормальной вероятностной бумаге (первый ряд справа). Действительно, для школ, имеющих среднюю оценку равную 45±10, экспериментальные данные лежат на теоретической прямой и существенные отклонения наблюдаются только для школ, набравших либо слишком мало, либо слишком много баллов. Во втором ряду слева приведены выборочные характеристики переменной, справа же приведен «ящик с усами» ˗ диаграмма размаха. На диаграмме (·) соответствует среднее значение, верхней и нижней стороне ящика соответствуют значениям , верхний и нижний «ус» равны , что соответствует 95% выборки. Результаты на рис. 2 приведены для выборки минимального объема, для выборок большего объема критерий нормальности еще более высоко значим.

Убедившись в корректности применения критерия Стьюдента, сравним оценки эффективности работы школ различных ОО. Полученные результаты структурированы и представлены в табл. 1.

Таблица 1

Сравнение результатов ЕГЭ разных ОО

Известно, что корректное применение t – теста требует не только нормального распределения двух выборок (показано выше), но и равенства дисперсий. В программе STATISTICA одновременно с критерием Стьюдента проверяется и критерий Фишера (равенства двух дисперсий). Результаты тестирования (столбцы 7 и 8 табл.2) свидетельствуют о том, что для всех переменных принимается нулевая гипотеза – отношение дисперсий равно 1, так как соответствующие вероятности существенно больше уровня значимости α = 0,05. Для наглядности все результаты в табл. 2, свидетельствующие о значимом отличии эффективных оценок различных ОО выделены полужирным шрифтом.

Проведенный анализ показал как ожидаемые, так и неожиданные результаты:

− оценки ЕГЭ по русскому языку для всех типов ОО значительно превышают 50 баллов (более 50% шкалы оценивания), в то же время лучшие оценки по математике значительно ниже 50%;

− оценки эффективности обучения в томских и городских ОО (население < 100 000), а также в городских и сельских ОО по русскому языку и математике можно считать статистически равными;

− знания русского языка у выпускников малокомплектных школ значимо ниже, чем томских и городских ОО;

− оценки по математике в малокомплектных школах значимо ниже, чем в томских и городских;

Б. Влияние контекстных факторов на образовательные результаты школьников

Оценка влияние контекстных факторов (переменных) на эффективность работы школ (оценки ЕГЭ по русскому языку и математике) решалась в рамках линейного корреляционного анализа. Для оценки тесноты связи между случайными переменными X и Y рассчитывался эмпирический коэффициент парных корреляций . Проверка гипотезы о статистически значимой корреляции осуществлялась для всех переменных при уровне значимости α = 0,05. Наглядное представление результатов (матрицы коэффициентов размерностью ~ 180 × 180) затруднено. Пример корреляционной матрицы для школ области и для факторов, характеризующих кадровое обеспечение школы, приведен в табл. 2.

Таблица 2

Корреляционная матрица (все школы области)

В таблице приведены значения коэффициентов парных корреляций (верхняя строка) и соответствующие вероятности принятия нулевой гипотезы (нижняя строка). Представленная матрица эмпирических коэффициентов корреляции свидетельствует о том, что линейной или «почти линейной» связи между переменными (факторами) и оценками эффективности работы школ не наблюдается. Лишь для некоторых факторов верна гипотеза H1 – коэффициент корреляции значимо отличается от нуля. Правда этот коэффициент, как правило, меньше 0.5 по модулю, что указывает на нелинейную связь переменных. Для дифференцированной оценки влияния факторов на эффективность работы школы корреляционные матрицы рассчитывались для всех типов ОО. Аналогичным образом все исследования были проведены для факторов, отвечающих за информационно – техническое обеспечение школы и социально – экономическое положение учащихся.

Корреляционный анализ оценивает степень взаимосвязи двух и более случайных величин, однако еще важнее найти модель этой связи, позволяющая предсказать значения одной случайной величины по конкретным значениям другой (других). Решение этой проблемы будем искать в рамках многомерного линейного регрессионного анализа.

На первом этапе построили одномерную регрессионную модель, в которой независимая переменная X - доля семей, где оба родителя имеют высшее образование, Y – средний балл по русскому языку. Переменная X выбрана из тех соображений, что для большинства типов ОО значение парных корреляций было максимальным. Гипотеза о линейной зависимости оценки эффективности работы школы от контекстного фактора иллюстрируется рис. 3.

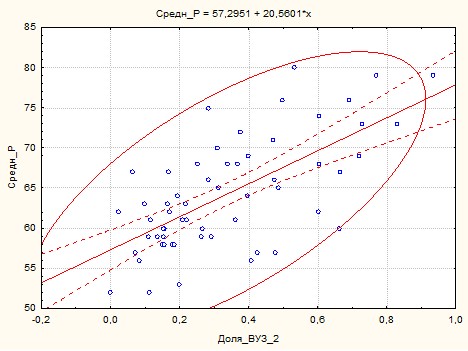
Рис. 3. Диаграмма рассеяния с подобранной прямой регрессии

Пунктирные линии соответствуют 95% доверительному интервалу для коэффициентов уравнения линейной регрессии. Эллипс рассеяния, построенный относительно линии регрессии накрывает 95% наблюдаемых точек. В заголовке приведено уравнение линейной регрессии, коэффициенты которого вычислены методом наименьших квадратов по заданной выборке (STATISTICA). Подробные характеристики модели приведены в табл. 3.

Таблица 3

Характеристики регрессионной модели (томские школы)

Коэффициент множественной корреляции R характеризует тесноту линейной связи между зависимой и всеми независимыми переменными. Коэффициент детерминации () и скорректированный коэффициент детерминации () выражает долю вариации зависимой переменной, объясненную данной моделью; критерий Фишера F характеризует значимость регрессии (нулевая гипотеза – между зависимой и независимыми переменными нет линейной зависимости). Эта гипотеза отклоняется, так как вероятность ее принятия p < 10-5 значительно меньше уровня значимости. Гипотезы о нулевых значениях коэффициентов уравнения также отклоняются из-за слишком малых вероятностей (столбец 7).

Значение коэффициента детерминации R2 = 0.445 очень мало, желательно, чтобы R2>0.8, к тому же только 67 % всей изменчивости объясняется вариацией переменной. Для решения данной проблемы построим многомерную линейную регрессионную модель.

На этапе корреляционного анализа были выявлены 10 – 12 контекстных факторов, связь которых с оценками эффективности работы школы была максимальной (максимум модуля коэффициента корреляции). Все модели созданы и исследованы для различных ОО.

Параметры модели максимальной размерности для ОО г. Томска приведены в табл. 4.

Таблица 4

Регрессионная модель (m=12)

Обсудим полученные результаты:

− в многомерной модели 82% всей изменчивости объясняется вариацией независимых переменных, в одномерной модели 67%;

− в многомерной модели , что значительно выше, чем в одномерной модели;

− при оценке качества коэффициентов многомерной модели только три значимо отличаются от нуля. Это коэффициенты при контекстных факторах, характеризующих, образовательный уровень родителей, долю учащихся, принимавших участие в олимпиадах и долю учащихся стоящих на учете.

Для выявления наиболее существенных объясняющих переменных применили следующий подход [3]: последовательно (пошагово) исключались наименее значимые переменные. В качестве оптимальной размерности модели (m) принималась та, для которой был максимален. Полученные результаты приведены в табл. 5.

Таблица 5

Оптимальная размерность линейной регрессионной модели

Очевидно, что характеристики модели зависят от ее размерности, при этом для различных оценок эта зависимость не одинакова. Следует отметить, что многомерные модели для школ разных ОО значительно отличаются. Прокомментируем полученные результаты:

• Качество многомерной регрессионной модели существенно зависит от типа ОО. Для томских школ характеристики модели максимальны для всех рассмотренных в работе оценок эффективности. Для городских школ области, за исключением томских, применение множественной регрессии – приемлемо. Однако уже для сельских школ, значение скорректированного коэффициента детерминации не достигает 0.25, а это значит, что менее 25% вариации описывается предложенной регрессионной моделью. Для малокомплектных школ это значение еще ниже, что говорит о некорректности применения линейных моделей для сельских и малокомплектных школ.
• Для всех оценок эффективности работы школы характеристики регрессионной модели – R и 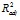ведут себя одинаково в зависимости от размерности (m).
• Оценки ЕГЭ по русскому языку для различных ОО значительно лучше описываются линейной регрессионной моделью, чем оценки по математике. При этом в зависимости от размерности модели значение коэффициента множественной корреляции для томских школ изменяется от 0.82 (m = 12) до 0.65 (m = 1). Соответствующие значения скорректированного коэффициента детерминации равны 0.59 и 0.41.

• Для сельских школ максимальный скорректированный коэффициент детерминации (контекстные факторы – социально – экономическое положение учащихся) не превышает 0.25, а для контекстных факторов – кадровое обеспечение школы – 0.14. Эти результаты подтверждают некорректность линейной модели (отсутствие влияния контекстных факторов на эффективность оценок) любой размерности для сельских школ.
• Для томских школ оценки ЕГЭ по математике более корректны для второго набора факторов – кадровое обеспечение школы (max 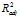= 0.535, min 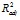= 0.341), чем для факторов – социально – экономическое положение учащихся (max 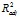= 0.309, min 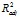= 0.18).

Выводы

1. Статистические исследования показали, что результаты городских и сельских школьников значимо различны, и не подлежат прямому сопоставлению. Результаты ЕГЭ школьников из малых (менее 100 000) городов и крупных (более 500 тыс. населения) городов отличаются незначительно.
2. Наиболее существенное влияние на образовательные результаты оказывают следующие факторы:
   1. Процент полных семей обучающихся в данной ОО;
   2. Процент родителей, имеющих высшее образование среди обучающихся в данной ОО;
   3. Процент обучающихся, состоящих на различных формах учета (инспекции КДН и пр.);
   4. Процент участия обучающихся в олимпиадах (конкурсах) различного уровня;
3. Показана эффективность методики [7] по оценке влияния различных факторов на образовательные результаты школьников;
4. Линейная многомерная регрессионная модель показала значительно более высокий коэффициент детерминации (около 58%), нежели одномерная (43, 5%). Но, тем не менее, очевидна необходимость дальнейшего исследования степени влияния отдельных факторов внутри различных групп ОО (городских, сельских и пр.).
5. Неудовлетворенность качеством многомерной регрессионной модели требует дальнейших исследований. Одним из возможных путей исследований представляется применение методов многомерного факторного и кластерного анализа, нелинейной регрессии.

Рецензенты:

Спицын В.Г., д.т.н., профессор кафедры Вычислительной техники Института Кибернетики ФГАОУ ВПО НИ ТПУ, г. Томск;

Уразаев А.М., д.б.н., профессор, ведущий научный сотрудник Томского государственного педагогического университета, г. Томск.

Библиографическая ссылка