В ряде мехатронных и робототехнических систем цель управления состоит в обеспечении технологического процесса, выполняемого по некоторой, заранее заданной или неопределенной, траектории с обеспечением требуемого вектора усилия при внешних флуктуирующих возмущениях. Эта проблема особенно актуальна в случаях, когда действительная траектория отличается от программной и требуется переход на фактическую, например, при управлении мобильными роботами, роботами для гидрорезания нефтепроводов, а также в технологическом оборудовании с большим моментом инерции и высокой динамикой.
Широкое распространение для САУ отмеченного типа получило управление, основанное на положениях теории инвариантности, в частности, управление, построенное на модифицированной четвертой форме инвариантности. По сравнению с другими методами коррекции введение инвариантных входов повышает точность, не изменяя свойств замкнутого контура системы. Реализация модифицированной четвертой формы инвариантности возможна использованием методов самонастройки, один из которых состоит в коррекции программной траектории, при ее разложении в интерполяторе на задающие для приводов воздействия, на стадии их формирования в устройстве формирования управляющего воздействия (УФУВ). Коррекция управляющего воздействия в устройстве его формирования выполняется на программном уровне и не влечет изменений основного контура привода, т.е. не затрагиваются внутренние свойства, а, следовательно, и динамические характеристики привода.
Принципиальное значение для рассматриваемого способа коррекция управляющей программы является процедура разложения заданной траектории на управляющие для приводов сигналы. Для оценки возможности реализации адаптивных алгоритмов управления составим дискретную модель работы УФУВ в режимах интерполяции. Рассмотрим формирование дополнительного управления, приводящие к коррекции программной траектории, в конечном итоге, к введению дополнительной составляющей в управляющее для приводов воздействие. Данный вопрос разберем на примере наиболее распространенного метода интерполяции - оценочной функции (ОФ) и для наиболее распространенных видов траектории - прямая линия и дуга окружности [2, 3].
Для организации управления вдоль заданной кривой (прямой) Z=f(X) отыскивается такая функция S, которая удовлетворяет условиям, обозначенным на рис. 1: 1) делит плоскость одного квадранта, где организуется управление, например XOZ, на две подплоскости U+ и U-; 2) в подплоскости S+ функция S > 0; 3) в подплоскости S- функция S < 0; 4) на заданной траектории функция S=0.
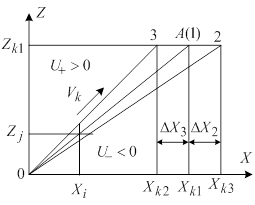
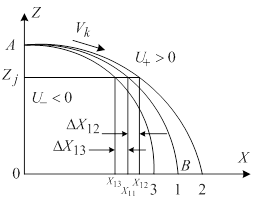
Рис. 1. Организация движения по методу ОФ
Алгоритм управления по ОФ предусматривает движение шагами по каждой координате в зависимости от знака ОФ в сторону, приближающую программную точку к идеальной траектории. В области всех значений аргументов это предусматривает вычисление ОФ, определение ее знака, и в зависимость от него формирование приращений Δx, Δz. На частоте f0 определяется новое значение ОФ согласно выражений
![]() при шаге по Z;
при шаге по Z;
![]() при шаге по X, (1)
при шаге по X, (1)
где знаки перед Xa, Za, определяются квадрантом.
Условия выполнения элементарных координатных приращений можно представить в виде:
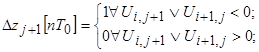
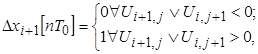 (2)
(2)
где: i, j — число предыдущих приращений соответственно по координатам X, Z.
На частоте 1/Тк формируется управляющее для привода воздействие. Из выражений (1) - (2) следует: 1) в формировании приращений используются только значения координат конечной точки Xa, Za, задаваемые в программе и являющиеся для данного участка константами; 2) для изменения траектории достаточно изменить значение одной из координат конечной точки - аргумента, причем независимо от метода интерполяции; 3) в силу принципа разложения заданного контура на управляющие воздействия и двухчастотного преобразования при изменении вектора положения автоматически изменяются проекции вектора скорости; 4) при неизменной в процессе выполнения технологической операции траектории достаточна разовая коррекция параметра Xa или Za.
При движении по дуге окружности метод ОФ определяет элементарные координатные приращения в виде
![]()
![]() (3)
(3)
где знаки перед вторым слагаемым определяются квадрантом и направлением движения.
В зависимости от знака ОФ приращения формируются в соответствии с логическими уравнениями
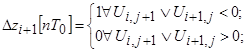
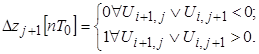 (4)
(4)
Из выражений (3) - (4) следует, что в отличие от линейной интерполяции здесь для формирования приращений используются текущие координаты Xi, Zi.
Особенности реализации. Большинство рассматриваемых технологических операций выполняются с постоянной или медленно изменяющейся скоростью. Тогда, составляющая моментной ошибки δΔf, обусловленная отклонением программной и фактической траекторий, может быть получена путем вычитания из текущей ошибки детерминированных составляющих ошибок: кинетической по управляющему и статической по возмущающим.
Рассмотрим сначала коррекцию при движении по прямолинейному участку в плоскости. Дополнительное управление Δgx должно выполняться за счет изменения значения координаты (функции) конечной точки Ха, используемой в процедурах (2), при получении интерполяционных импульсов. Новое значение Ха* определяется как
![]() ,
,
где знак "+" или "-" определяется знаком моментной минимизируемой ошибки.
Дополнительная составляющая ΔХа будет определяться
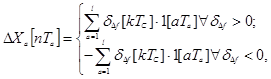 (5)
(5)
где l – число шагов до выполнения условия δΔf =0. Здесь частота Ta определяет частоту изменения Ха в соответствующей ячейке памяти.
При движении по дуге окружности коррекция значений текущей координаты функции (координаты) изменяется аналогично по зависимости
![]() .
.
Данный метод адаптации рассмотрен на примере двух структур, представленных на рис. 2. На схемах обозначены: W1(p) – передаточная функция привода с кинематической передачей и объектом управления; V(p) – передаточная функция привода по возмущению; K(p) – передаточная функция звена адаптации управляющего сигнала; g0, f – управляющее и возмущающее воздействия привода соответственно; X, X0 – непосредственно регулируемая координата и координата смежного привода соответственно; δ – суммарная ошибка системы; Δf – отклонение фактического усилия от расчетного; δf0 – составляющая ошибки системы, обусловленная возмущающим воздействием; δΔf – моментная составляющая ошибки; Δg – дополнительная составляющая управляющего воздействия.
В зависимости от управляющего воздействия звено K(p) имеет передаточную функцию:
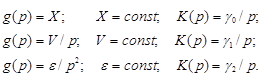
Где: X – регулируемая координата исследуемого привода; V – скорость входного сигнала исследуемого привода; ε – ускорение исследуемого привода; γ0, γ1, γ2 – коэффициенты передачи в канале формирования дополнительного управления.
Моделирование структур (рис.2) с каналом адаптации сигнала задания по положению, скорости и ускорению было реализовано в среде пакета программы MatLab – Simulink. В частности, проводился анализ точности системы управления в режиме движения с постоянной скоростью и при отработке гармонического входного сигнала. В роли объекта исследования выступает привод перемещения с главной обратной связью по положению исполнительного механизма. Привод включает в себя два внутренних контура: по напряжению и частоте вращения двигателя и ПИД регулятор.
Главное возмущающее воздействие, обусловлено геометрически-силовым взаимовлиянием координатных приводов, вызывающим отклонение фактической траектории исполнительного органа от заданной. В качестве привода смежной координаты выступает симулятор межкоординатных возмущений. В зависимости от вида сигнала задания его выходная координата описывается уравнениями:
Случай 1. Канал адаптации по положению
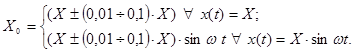
Случай 2. Канал адаптации по скорости
![]()
Случай 3. Канал адаптации по ускорению
![]()
Где: X0 – координата смежного привода; V0 – скорость привода второй координаты; ε0 –ускорение симулятора межкоординатных возмущений.
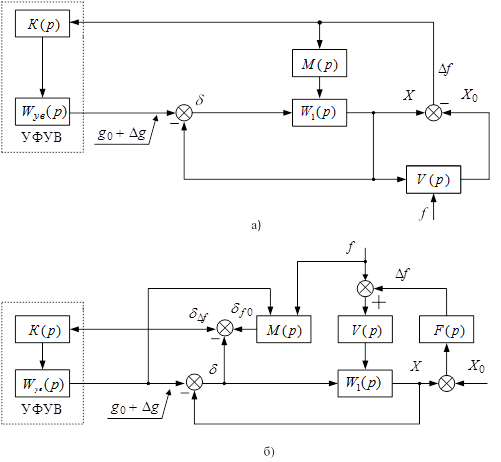
Рис. 2. Структурные схемы САУ с коррекцией управляющего воздействия привода в устройстве его формирования
Исследования проводились в режиме изменения момента нагрузки Mн(t), обусловленного влиянием «другой» координаты, в интервале от 1 до 5 Нм (при номинальном моменте привода 2 Нм). В ходе моделирования плавно изменялась скорость задания управляющего воздействия в диапазоне 10…80 мм/с для каналов адаптации по положению и скорости, а также ускорение входного сигнала в пределах от 1 до 20 мм/с2 для канала адаптации по ускорению. Соотношение координат, скоростей и ускорений приводов варьировалось от 1 до 10 %. Исследуемый привод в режиме движения с постоянной скоростью имеет ошибку положения, обусловленную влиянием симулятора смежной координаты и изменяющуюся в пределах от 5 до 10 %. Результаты моделирования САУ в режиме отработки гармонического входного сигнала показали, что вследствие внешних межкоординатных возмущений на выходе системы управления наблюдается установившаяся динамическая ошибка (10 % от амплитуды задающего сигнала). Данные показатели не отвечают требованиям, предъявляемым к системам управления отмеченного типа. Введение контура адаптации позволяет свести к минимуму влияние внешних возмущений при выполнении технологического процесса по заранее заданной траектории и при необходимости осуществить переход на новую траекторию. На рис. 3 представлены графики изменения выходной координаты привода с контуром адаптации и без него, в режиме движения с постоянной скоростью и при отработке САУ гармонического входного сигнала. На рис. 2 цифрами обозначены: 1 – график изменения выходной координаты САУ без контура адаптации; 2 – график изменения выходной координаты САУ с контуром адаптации; 3 – отклонение положения инструмента Δx от заданной траектории. Рис. 4 демонстрирует графики изменения показателей САУ в течение времени процесса компенсации. На рис. 4,а представлены основные показатели САУ для канала адаптации по положению, при tпк = 5с, V=10 мм/с, Δx=5%, Mн = 5 Нм. На рис. 4,б изображены основные показатели САУ для канала адаптации по скорости, при tпк = 5с, v=10 мм/с, v/v0 =5%, Mн = 5 Нм. На рис. 4,в показаны основные показатели САУ для канала адаптации по ускорению, при tпк = 5с, ε=5 мм/с2, ε / ε0 =10% , Mн = 5 Нм.
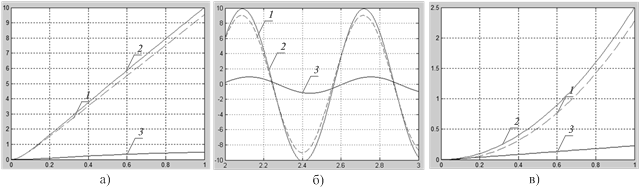
Рис.3. Исследование показателей точности САУ:
а) графики изменения выходной координаты САУ в режиме движения с постоянной скоростью, для каналов адаптации по скорости и положению (V=10 мм/с, Δx=5%, Mн = 5 Нм); б) графики изменения выходной координаты САУ при отработки гармонического входного сигнала для канала адаптации по положению (А=10, ω=10 рад/с, Mн = 5 Нм); в) графики изменения выходной координаты САУ для канала адаптации сигнала задания по ускорению (ε=5 мм/с2, ε / ε0 =10% , Mн = 5 Нм)
В ходе моделирования получены зависимости коэффициента передачи звена K(p) в канале адаптации от скорости (частоты) задающего воздействия для контура адаптации по скорости и положению, а также от ускорения сигнала задания для контура адаптации по ускорению. На рис. 5 представлен график зависимости коэффициента передачи от частоты задающего воздействия при отработке гармонического сигнала соответственно.
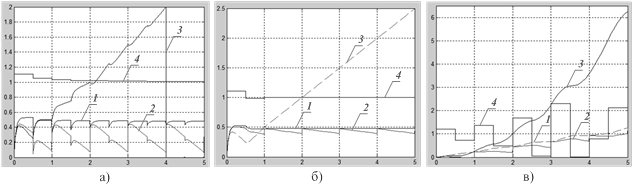
Рис. 4:
1 – график изменения ошибки системы управления δ; 2 – график моментной составляющей ошибки δΔf; 3 – график отклонения фактического усилия от расчетного Δf; 4 – график изменения коэффициента коррекции управляющего сигнала g*
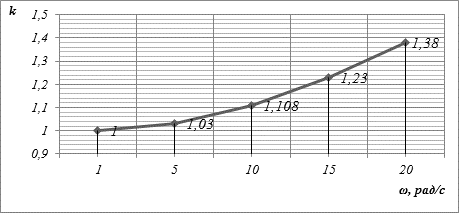
Рис. 5. График изменения коэффициента коррекции управляющего сигнала, в зависимости от частоты сигнала задания
Выводы
1. Применение четвертой формы инвариантности в мехатронных и робототехнических системах дает возможность выполнение динамической коррекции движения.
2. Исследуемый способ реализации контура адаптации, предусматривает коррекцию уровней сигналов производных на стадии формирования управляющего воздействия в процессе выполнения технологического процесса.
3. Коррекция управляющего воздействия в устройстве его формирования выполняется на программном уровне и не влечет изменений основного контура привода, т.е. не затрагиваются внутренние свойства, а, следовательно, и динамические характеристики привода. Причем, эта коррекция носит разовый характер при неизменной фактической траектории.
4. Результаты проведенных исследований подтверждают работоспособность рассмотренных алгоритмов.
Рецензенты:
Гоц А.Н., д.т.н., профессор кафедры «Тепловые двигатели и энергетические установки», ФГБОУ ВПО «Владимирский государственный университет имени Александра Григорьевича и Николая Григорьевича Столетовых», г. Владимир;
Новоселов Б.В., д.т.н., профессор, главный научный сотрудник ОАО «ВНИИ «СИГНАЛ», г. Ковров.
Библиографическая ссылка
Кобзев А.А., Новикова Н.А., Лекарева А.В., Махфуз А.А. АНАЛИЗ АЛГОРИТМОВ КОРРЕКЦИИ ПРОГРАММНОЙ ТРАЕКТОРИИ В УСТРОЙСТВЕ ФОРМИРОВАНИЯ УПРАВЛЯЮЩЕГО ВОЗДЕЙСТВИЯ ДЛЯ ПРИВОДОВ РОБОТОТЕХНИЧЕСКИХ СИСТЕМ // Современные проблемы науки и образования. 2014. № 6. ;URL: https://science-education.ru/ru/article/view?id=15702 (дата обращения: 06.07.2025).



