Волноводные структуры широко используются в системах обработки информации различных частотных диапазонов. Особое место занимают структуры с невзаимными свойствами, на основе которых разработаны элементы развязок устройств (вентили, циркуляторы и др.). Для создания этих устройств необходимы гиротропные среды. Наиболее распространенными являются ферриты, диапазон использования которых ограничен СВЧ и КВЧ диапазонами. В данной работе показаны невзаимные свойства волноводной структуры с тонкими пленками сверхпроводника второго рода и диэлектрика с нелинейными параметрами. Показана возможность существования в рассмотренной структуре солитоноподобных импульсов, параметры которых зависят от дисперсионных характеристик волноводной структуры, а также от амплитуды импульсов.
Тонкая пленка сверхпроводника в резистивном состоянии и тонкая пленка диэлектрика с нелинейными параметрами εxx =εyy =ε+α3|E| 2+α5|E| 4 +...расположены параллельно узким стенкам прямоугольно волновода. Внешнее магнитное поле В направлено параллельной широким стенкам волновода, транспортный ток в сверхпроводнике параллелен узкой стенке волновода. Рассмотрена Н-волна (с компонентами Hx, Hz, Ey), которая эффективно взаимодействует с вихревой структурой в сверхпроводнике.
Наличие тонкого сверхпроводящего слоя в смешанном состоянии учитывается введением граничных условий:
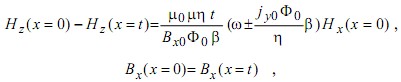
где jy0 - плотность транспортного тока в сверхпроводнике, β - продольное волновое число, σ - проводимость сверхпроводящей пленки, Ф0 - квант магнитного потока, η - коэффициент вязкости магнитного вихря. Знаки «+» и «-» соответствуют прямой и обратной волне.
Задача сводится к решению нелинейного интегро - дифференциального уравнения относительно функции Ey(z,t)
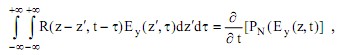
где ядро интегрального оператора R(z,t) представляет собой обратное преобразование Фурье определяемой аналитическим путем функции R(ω,β):
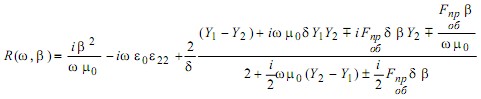
При учетe нелинейности третьего порядка уравнение принимает вид
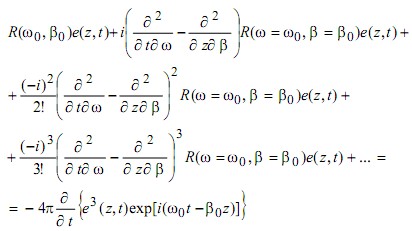
и представляет собой обобщение нелинейного уравнения Шредингера. Решением уравнения является функция e(z,t,)=Escn(Z,k), описывающая решетку нелинейных импульсов при α3γ2(R)<0, или e(z,t)=Essn(z,k) (импульсы затемнения) при α3γ2(R) >0,
Длительность импульсов ![]()
скорость импульсов 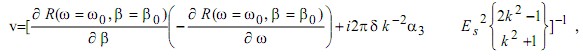
Проведен численный анализ. С ростом амплитуды импульсов длительность уменьшается, что характерно для солитонов в безграничных средах. В качестве сверхпроводящей пленки рассмотрены пленки YBa2Cu3O7. Продолжительность импульса τ уменьшается с ростом толщины сверхпроводящей пленки, а скорость v имеет максимум при определенной толщине пленки t. При увеличении несущей частоты импульса уменьшается продолжительность импульса и его скорость. При увеличении толщины t также наблюдается существенное уменьшение затухания. Параметрами импульсов в волноводных структурах можно управлять, меняя плотность тока транспорта в пленке и поле подмагничивания. Кроме того, структура обладает невзаимными свойствами для волн, распространяющихся в прямом и обратном направлениях, которые можно реализовать в различных областях частот. В зависимости от толщины сверхпроводящей пленки импульс может менять свое направление распространения на противоположное, что соответствует изменению знака скорости v. С ростом постоянного внешнего магнитного поля продолжительность импульса т уменьшается, а скорость v достигает максимума при определенном значении Bx0, причем импульс может менять направление распространения.
В волноводной системе с тонкой пленкой сверхпроводника в резистивном состоянии энергия может передаваться импульсу за счет энергии движения решетки вихрей Абрикосова. Возможность усиления электромагнитной волны за счет энергии решетки вихрей Абрикосова была показана в работах [1,2]. Использование в волноводных структурах двухслойных тонких пленок сверхпроводник - диэлектрик типа Керра позволяет формировать нелинейные стационарные импульсы малой продолжительности с высокой скоростью распространения, параметры которых зависят от дисперсионных характеристик волноводной структуры, величины коэффициента нелинейности, а также от амплитуды импульсов Es. В зависимости от величины параметров нелинейной пленки, величины магнитного поля продолжительность нелинейного импульса может достигать порядка 10-12 с, а скорость его распространения порядка 108 м/с.
Литература
1. Глущенко А.Г., Головкина М.В. Отражение электромагнитной волны слоистой структурой сверхпроводник - диэлектрик. // Письма в ЖТФ. -1998. - Т. 24. - Вып. 1. - С. 9-12.
2. Glushchenko A.G., Golovkina M.V. Electromagnetic wave propagation in superconductor -dielectric multilayers. // Symposium Proceedings "EMC'98 ROMA". - Rome. - Italy. -1998. International Symposium on Electromagnetic Compatibility "EMC'98 ROMA" Rome. - Italy. - 1998. - V 2. - P. 483-486.
Библиографическая ссылка
Глущенко А.Г., Головкина М.В. НЕВЗАИМНЫЕ СВОЙСТВА ВОЛНОВОДНОЙ СТРУКТУРЫ С ПЛЕНКАМИ СВЕРХПРОВОДНИКА ВТОРОГО РОДА И НЕЛИНЕЙНОГО ДИЭЛЕКТРИКА // Современные проблемы науки и образования. 2005. № 1. ;URL: https://science-education.ru/ru/article/view?id=157 (дата обращения: 29.10.2025).



