В настоящее время автоматическая обработка изображений является одним из важнейших направлений в области искусственного интеллекта и подразумевает разработку робототехнических комплексов, осуществляющих распознавание образов. Одним из наиболее эффективных инструментов для распознавания образов является системы, построенные на нечеткой логике и искусственных нейронных сетях. В системе технического зрения (СТЗ) необходимо нескольких методов и алгоритмов, решающие одну и ту же задачу различными способами, обеспечивая при этом необходимые показатели по быстродействию и достоверности идентификации [1-3].
Сущность гибридного алгоритма обработки изображений в СТЗ мобильного робототехнических комплексов (МРК) заключается в приведении исходного изображения сцены к виду, позволяющему решить задачу распознавания ее объектов.
Алгоритм предварительной обработки изображения с помощью нечеткой системы в СТЗ
К обработке изображений нечеткая обработка представляет собой множество различных нечетких подходов, которыми являются понимание, представление, обработки изображений, сегменты и нечеткие множества. В процессе распознавания образов огромное значение имеет процесс предварительной нечеткой обработки изображений, так как именно от него зависит качество данных, далее поступающих на входы нейронной сети. В рамках решаемой задачи, разработанный алгоритм предварительной нечеткой обработки можно представить в виде следующей последовательности шагов (рис. 1): захват изображения с помощью веб-камеры; преобразование полученного цветного изображения в изображение в градациях серого цвета; нечеткая обработка изображений.
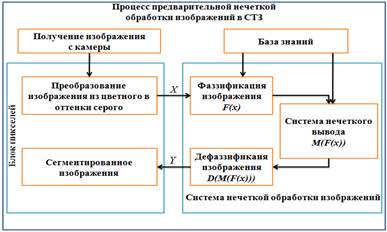
Рис. 1. Алгоритм предварительной нечеткой обработки изображения
Таким образом, первым шагом предварительной нечеткой обработки является преобразование изображение из цветного в оттенки серого. Преобразование цветов изображения в оттенки серого цвета осуществляется следующим образом. Вся цветовая палитра представляется в виде куба, вершины которого соответствуют различным цветам. Серая шкала располагается на диагонали куба, соединяющей черную и белую вершины.
Для преобразования изображения в оттенки серого для каждой точки изображения выделяются интенсивности красной, зеленой и синей составляющей цвета, а затем осуществляется преобразование цвета по следующей формуле:
![]() (1)
(1)
где ![]() – новое значение цвета,
– новое значение цвета, ![]() – интенсивность красной составляющей цвета,
– интенсивность красной составляющей цвета, ![]() – интенсивность зеленой составляющей цвета, а
– интенсивность зеленой составляющей цвета, а ![]() – интенсивность синей составляющей цвета. Выход каждого алгоритма оттенки серого между 0 и 1. Для преобразования изображений в использующие только оттеки серого существует некоторые методов. В методе определения светлоты используется среднее значение между двумя наиболее и наименее значимыми цветами:
– интенсивность синей составляющей цвета. Выход каждого алгоритма оттенки серого между 0 и 1. Для преобразования изображений в использующие только оттеки серого существует некоторые методов. В методе определения светлоты используется среднее значение между двумя наиболее и наименее значимыми цветами: ![]() . В методе среднего используется среднее значение всех трёх цветов:
. В методе среднего используется среднее значение всех трёх цветов: ![]() . В методе определения яркости используется взвешенное среднее значение всех трех цветов, учитывающее человеческое восприятие. Так, поскольку человеческий глаз наиболее восприимчив к зеленому цвету, его вес считается наиболее важным:
. В методе определения яркости используется взвешенное среднее значение всех трех цветов, учитывающее человеческое восприятие. Так, поскольку человеческий глаз наиболее восприимчив к зеленому цвету, его вес считается наиболее важным: ![]() . Метод определения яркости используется программное обеспечение для обработки изображений. Он реализован функцию «rgb2gray» в среде MATLAB и это часто используется для компьютерного зрения [4]. В процессе предварительной нечеткой обработки имеет процесс преобразования изображений из цветного (RGB) в оттенки серого с помощью метода определения яркости. Далее изображение преобразуется из оттенки серого в черно-белый [0 1] (рис. 2).
. Метод определения яркости используется программное обеспечение для обработки изображений. Он реализован функцию «rgb2gray» в среде MATLAB и это часто используется для компьютерного зрения [4]. В процессе предварительной нечеткой обработки имеет процесс преобразования изображений из цветного (RGB) в оттенки серого с помощью метода определения яркости. Далее изображение преобразуется из оттенки серого в черно-белый [0 1] (рис. 2).
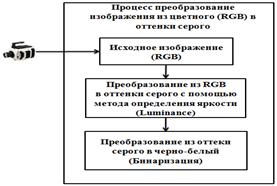
Рис. 2. процесс преобразования изображений из цветного в оттенки серого
Бинаризация изображения при предварительной обработке
Целью предварительной нечеткой обработки изображения является формирование и последующее улучшение изображения, его бинаризация и кодирование (в частности, получение контурного представления). Бинаризация изображения представляет собой процесс преобразования изображения, состоящего из градации одного цвета (в нашем случае - серого), в бинарное изображение, т.е. изображение, в котором каждый пиксель может иметь только два цвета (в нашем случае это черный и белый цвета). В результате такого преобразования, цвет пикселя условно считают равным нулю или единице, при этом, пиксели с нулевым значением (в данном случае это пиксели белого цвета) называют задним планом, а пиксели со значением равным единице (черного цвета) называют передним планом. Но бинарное изображение, полученное в результате такого преобразования, искажается, по сравнению с оригиналом, что характеризуется появлением разрывов и размытостей на объектах, возникновением зашумлений изображения в однородных областях, а так же к потере целостности структуры объектов.
Потеря целостности объекта, а так же разрыв объекта, возникают в силу ряда причин, таких как, большая неравномерность освещения объекта или касание (или наложение объектов друг на друга). Особую сложность в обработке вызывает именно наложение (или касание – как частный случай наложения), т.к. с одной стороны, изображение нескольких объектов может быть интерпретировано как один объект, а с другой стороны, алгоритмы, проверяющие геометрическую целостность объекта, в местах наложения будут формировать разрывы, представляя эти области в виде заднего плана. Сложность обработки заключается в отсутствии теоретического решения задачи интерпретации наложения объектов, так как часть информации утеряна. В реализации алгоритмов на практике, в качестве верного решения принимают один из указанных вариантов – либо пересечение считается продолжением текущего объекта, либо область наложения будет считаться задним планом.
Пороговая обработка преобразовывает цветовое или серое изображение в черно-белое изображение. Пороговые преобразования занимают центральное место в прикладных задачах сегментации изображений благодаря интуитивно понятным свойствам и простоте реализации. Для каждого пикселя в изображении, его уровень интенсивности исследован, если его значение – выше некоторого порогового уровня, это соответствует белому цвету. Если это – ниже порога набора, это установлено в черный. Пороговый уровень будет между 0 и 255.
В настоящее время существует большое количество методов бинаризации. Суть данного преобразования растровых изображений заключается в сравнительном анализе яркости текущего пикселя ![]() с неким пороговым значением
с неким пороговым значением ![]() : если яркость текущего пикселя превышает пороговое значение, т.е.
: если яркость текущего пикселя превышает пороговое значение, т.е. ![]() , то цвет пикселя на бинарном изображении будет белым, в противном случае цвет будет черным. Пороговой поверхностью
, то цвет пикселя на бинарном изображении будет белым, в противном случае цвет будет черным. Пороговой поверхностью ![]() является матрица, размерность которой соответствует размерности исходного изображения [5].
является матрица, размерность которой соответствует размерности исходного изображения [5].
В процессе бинаризации все методы делятся на две группы по принципу построения пороговой поверхности – это методы глобальной и локальной обработки бинаризации. В методах глобальной обработки бинаризации пороговая поверхность является плоскостью с постоянным значением пороговой яркости, т.е. значение порога рассчитывается исходя из анализа гистограммы всего изображения и является одинаковым для всех пикселей исходного изображения. Глобальная пороговая обработка имеет существенный недостаток - если исходное изображение имеет неоднородное освещение, области, которые освещены хуже, целиком классифицируются как передний план. В локальных же методах обработки бинаризации пороговое значение меняется для каждой точки исходя из некоторых признаков области, принадлежащей некоторой окрестности данной точки. Недостатком такого рода преобразований является низкая скорость работы алгоритмов, связанная с пересчетом пороговых значений для каждой точки изображения.
В качестве метода для решения поставленной задачи воспользуемся методом Бернсена [4,5]. Метод базируется на идее сопоставления уровня яркости преобразуемого пикселя со значениями локальных средних, вычисляемых в его окружении. Пиксели изображения обрабатываются поочередно путем сравнения их интенсивности со средними значениями яркости в окнах с центрами в точках ![]() (рис.3).
(рис.3).
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3. Преобразование пикселя изображения
Алгоритм нечеткой обработки для выделения границ и сегментации изображений
После преобразования изображения в черно-белый, получается градиентное изображение с помощью оператора Собеля и поступается на входы нечеткого обработки изображения (НОИ) (рис. 4).
Нечеткая обработка изображений состоит из трех основных этапов: фаззификация изображений ![]() , система нечеткого вывода
, система нечеткого вывода ![]() на значениях принадлежности и дефаззификация изображений
на значениях принадлежности и дефаззификация изображений ![]() . Главная нечеткая обработка изображений находится в среднем шаге (система нечеткого вывода
. Главная нечеткая обработка изображений находится в среднем шаге (система нечеткого вывода ![]() ). После передачи данных изображения из серого уровня в фаззификацию, система нечеткого вывода определяется значениям принадлежности. Фаззификация – кодирование данных изображений и дефаззификация – декодирование результатов, которые позволяют обрабатывать изображения с нечеткими методами.
). После передачи данных изображения из серого уровня в фаззификацию, система нечеткого вывода определяется значениям принадлежности. Фаззификация – кодирование данных изображений и дефаззификация – декодирование результатов, которые позволяют обрабатывать изображения с нечеткими методами.
Изображение ![]() – размер
– размер ![]() с
с ![]() серыми уровнями
серыми уровнями ![]() и может быть определено как массив нечеткое одноточечное множество (нечеткие множества можно поддерживать только с одной точкой), указывающее значение принадлежности каждого пикселя в отношении по заранее свойства изображения (например – яркость, гладкость и т.д.).
и может быть определено как массив нечеткое одноточечное множество (нечеткие множества можно поддерживать только с одной точкой), указывающее значение принадлежности каждого пикселя в отношении по заранее свойства изображения (например – яркость, гладкость и т.д.).
![]()
![]() (1)
(1)
где ![]() и
и ![]() – принадлежности пикселя
– принадлежности пикселя ![]() в обозначении нечетких множеств. Определение значений принадлежности зависит от конкретных требований особенного применения и от соответствующей базы знаний.
в обозначении нечетких множеств. Определение значений принадлежности зависит от конкретных требований особенного применения и от соответствующей базы знаний.
Выход системы ![]() для входной системы
для входной системы ![]() задается следующую формулу:
задается следующую формулу:
![]() (2)
(2)
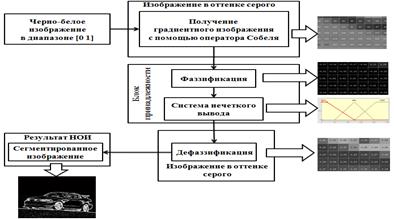
Рис. 4. Алгоритм нечеткой обработки изображений для выделения границ
Применение нейронных сетей для распознавания образов
Многослойным персептроном называют искусственную нейронную сеть, состоящую из нескольких входных узлов, образующих входной слой, одного или нескольких вычислительных слоев нейронов и одного выходного слоя (рис. 6). В таких сетях сигнал, подающийся на входной слой, передается последовательно в прямом направлении от слоя к слою. Данный тип ИНС успешно применяется для решения разнообразных задач, в частности для задачи распознавания образов [4].
Нейронная сеть обратного распространения ошибки состоит из нескольких слоев нейронов, причем каждый нейрон предыдущего слоя связан с каждым нейроном последующего слоя. В таких сетях, после определения количества слоев и количества элементов каждого слоя, требуется вычислить значения весов и порогов сети таким образом, что бы минимизировать ошибку прогноза. Данная задача решается при помощи разнообразных алгоритмов обучения. Суть этих алгоритмов заключается в подгонке сети к обучающим данным. Ошибка реализованной сети будет определяться путем прогона всех входных данных и сравнением реально полученных значений на выходе сети с целевыми значениями. Затем полеченные разности суммируются в общую, так называемую, функцию ошибок, которая характеризует общую ошибку сети. Но чаще, в качестве функции ошибок, берется сумма квадратов ошибок.
Одним из наиболее распространенных алгоритмов обучения многослойных нейронных сетей является алгоритм обратного распространения ошибки. В этом алгоритме вычисляется вектор градиента поверхности ошибок. Затем продвигаемся на некоторую величину в направлении вектора (он будет указывать нам направление наискорейшего спуска), где значение ошибки будет уже меньше. Такое последовательное продвижение постепенно приведет к минимилизации ошибки. Здесь возникает трудность с определением величины, на которую следует продвигаться. Если величина шага будет относительно большой, это приведет к наискорейшему спуску, однако есть вероятность «перепрыгнуть»
искомую точку или уйти в неверном направлении, если поверхность имеет достаточно сложную форму. Например, в случае, если поверхность представляет собой узкий овраг с крутыми склонами, алгоритм будет очень медленно продвигаться, прыгая с одного склона на другой. Если же величина шага будет маленькой, это приведет к нахождению наиболее оптимального направления, однако может значительно увеличить число итераций. Для достижения наиболее оптимального результата величина шага берется пропорционально крутизне склона с некоторой константой- скоростью обучения. Выбор этой константы осуществляется экспериментальным путем и зависит от условий конкретной задачи.
Введем следующие обозначения. Матрицу весовых коэффициентов от входов к скрытому слою обозначим ![]() , а матрицу весов, соединяющих скрытый и выходной слой –
, а матрицу весов, соединяющих скрытый и выходной слой – ![]() . Для индексов примем следующие обозначения: входы будем нумеровать только индексом
. Для индексов примем следующие обозначения: входы будем нумеровать только индексом ![]() , элементы скрытого слоя – индексом
, элементы скрытого слоя – индексом ![]() , а выходы – индексом
, а выходы – индексом ![]() . Число входов сети равно
. Число входов сети равно ![]() , число нейронов в скрытом слое –
, число нейронов в скрытом слое – ![]() , число нейронов в выходном слое –
, число нейронов в выходном слое – ![]() . Пусть сеть обучается на выборке
. Пусть сеть обучается на выборке ![]() ,
, ![]() . Тогда алгоритм обучения многослойного персептрона будет выглядеть следующим образом [5]:
. Тогда алгоритм обучения многослойного персептрона будет выглядеть следующим образом [5]:
Шаг 1. Инициализация сети. Весовым коэффициентам присваиваются малые случайные значения, например, из диапазона (-0.3, 0.3); задаются ![]() – параметр точности обучения,
– параметр точности обучения, ![]() – параметр скорости обучения (как правило,
– параметр скорости обучения (как правило, ![]() и может еще уменьшаться в процессе обучения),
и может еще уменьшаться в процессе обучения), ![]() – максимально допустимое число итераций.
– максимально допустимое число итераций.
Шаг 2. Вычисление текущего выходного сигнала. На вход сети подается один из образов обучающей выборки, и определяются значения выходов всех нейронов нейросети.
Шаг 3. Настройка синоптических весов. Рассчитать изменение весов для выходного слоя нейронной сети по формулам:
![]() где
где ![]() ,
, ![]() . Рассчитать изменение весов для скрытого слоя по формулам:
. Рассчитать изменение весов для скрытого слоя по формулам:![]() , где
, где ![]()
Шаг 4. Шаги 2-3 повторяются для всех обучающих векторов. Обучение завершается по достижении для каждого из обучающих образов значения функции ошибки, не превосходящего е или после максимально допустимого числа итераций.
На шаге 2 векторы из обучающей последовательности лучше предъявлять на вход в случайном порядке.
Количество входов и выходов сети, как правило, диктуется условиями задачи, а размер скрытого слоя находят экспериментально. Обычно число нейронов в нем составляет 30-50% от числа входов. Слишком большое количество нейронов скрытого слоя приводит к тому, что сеть теряет способность к обобщению (она просто досконально запоминает элементы обучающей выборки и не реагирует на схожие образцы, что неприемлемо для задач распознавания). Если число нейронов в скрытом слое слишком мало, сеть оказывается просто не в состоянии обучиться.
Заключение
Рассмотрены основные проблемы, а также пути их решения при первичной подготовке изображения к распознаванию. Детально разобраны алгоритм предварительной обработки с помощью нечеткой логики и процесс бинаризации изображения. Построен алгоритм нечеткой обработки для выделения границ в изображении с помощью оператора Собеля.
Рецензенты:
Гагарина Л.Г., д.т.н., профессор, заведующий кафедрой «Информатика и программное обеспечение вычислительных систем» Национального исследовательского университета «МИЭТ», г. Москва.
Портнов Е.М., д.т.н., профессор кафедры «Информатика и программное обеспечение вычислительных систем», начальник научно-исследовательской лаборатории «Управляющие информационные системы» Национального исследовательского университета «МИЭТ», г. Москва.
Библиографическая ссылка
Аунг Ч.Х., Тант З.П., Федоров А.Р., Федоров П.А. РАЗРАБОТКА АЛГОРИТМОВ ОБРАБОТКИ ИЗОБРАЖЕНИЙ ИНТЕЛЛЕКТУАЛЬНЫМИ МОБИЛЬНЫМИ РОБОТАМИ НА ОСНОВЕ НЕЧЕТКОЙ ЛОГИКИ И НЕЙРОННЫХ СЕТЕЙ // Современные проблемы науки и образования. 2014. № 6. ;URL: https://science-education.ru/ru/article/view?id=15579 (дата обращения: 12.01.2026).



