Компьютерная графика всегда решала и продолжает решать проблемы, связанные не только с индустрией развлечений, но и создавать детские обучающие программы, повышать эффективность работы людей творческих профессий (архитекторов и дизайнеров), и что самое главное – помогать людям, не имеющим по физическим причинам полноценной вовлеченности в окружающий их мир. Именно поэтому, исследования в данной области всегда будут актуальными.
Любое графическое представление объектов 3D сцены в связи с ограниченностью вычислительных ресурсов является приближенным решением специального интегрального уравнения – “уравнения рендеринга”. Среди всего множества алгоритмов, выделяют так называемые “непредвзятые”, копирующие физическую модель распространения света из реального мира, и, таким образом, снижающие погрешность в результирующем изображении – позволяя добиться “фотореалистичности”.
Главной проблемой “непредвзятости” является необходимость в действительно больших объемах вычислений, а значит и невозможность обработки алгоритмов непредвзятого 3Dрендеринга в режиме реального времени. Такой режим просто необходим в случае интерактивных приложений, основанных на непрерывном, “интерактивном” взаимодействии с пользователем (военные симуляторы, программы обучения вождению и многие др.).
Таким образом, объектом исследования данной работы выступают алгоритмы непредвзятого 3Dрендеринга как единственные, позволяющие получить максимально реалистичное или “фотореалистичное” изображение в компьютерной графике.
Простейший алгоритм по методу “бросания лучей (raycasting)”
Как было отмечено в ходе анализа современного состояния области непредвзятого 3Dрендеринга – все алгоритмы рендеринга являются всего лишь некоторым приближением, или аппроксимацией, главного уравнения рендеринга[1]:
![]() (1)
(1)
где: ![]() –количество энергии света, излучаемого из точки
–количество энергии света, излучаемого из точки ![]() в направлении вектора
в направлении вектора ![]() ;
; ![]() – двунаправленная функция отражательной способности поверхности, которая показывает количество энергии, передаваемой в ходе отражения света в точке
– двунаправленная функция отражательной способности поверхности, которая показывает количество энергии, передаваемой в ходе отражения света в точке ![]() из
из![]() в направлении
в направлении ![]() (зависит от свойств материала поверхности);
(зависит от свойств материала поверхности); ![]() –количество энергии света, пришедшего в точку
–количество энергии света, пришедшего в точку ![]() с направления
с направления ![]() ;
; ![]() – косинус угла между нормалью поверхности в точке
– косинус угла между нормалью поверхности в точке ![]() и “входящим” направлением
и “входящим” направлением ![]() .
.
Другими словами, количество энергии света, попадающего в глаз наблюдателя из любой точки сцены, складывается из двух факторов: энергии излучаемой из этой точки, а также – отраженной. Последняя зависит от BRDFматериала поверхности, на которой лежит точка, а также направления поступающего в нее света (вклад вносят все лучи, попадающие в полусферу с центром в этой точке).
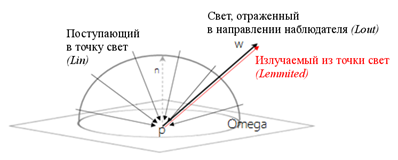
Рисунок 1. Визуализация главного уравнения рендеринга
Таким образом, решение главного уравнения рендеринга согласно методу “бросания лучей (raycasting)” при допущении, что все объекты сцены излучают свет, может быть записано, как:
![]() , (2)
, (2)
Видно, что в расчете (2) участвует лишь левое слагаемое суммы (1), что делает метод бросания лучей действительно простым, но сильно “предвзятым”. Вкратце, данный метод заключается в эмиссии лучей из глаза наблюдателя в направлении сцены таким образом, что каждый луч проходит через один пиксель экрана наблюдателя. Пересекаясь с объектами сцены, лучи добавляют их цвета в соответствующие пиксели (согласно допущению, сделанному ранее об эмиссии света всеми объектами сцены). Этот процесс показан нарис. 2.
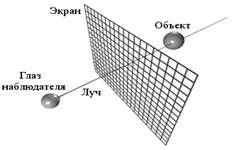
Рисунок 2. Метод “бросания лучей (raycasting)”
Тогда, алгоритм трассировки лучей по методу “бросания лучей” может быть представлен на рис. 3. Из схемы ясно, что операции над конкретными пикселями экрана наблюдателя, вообще говоря – одинаковы, но что более важно – независимы. Принимая во внимание одно из главных условий задачи диссертации, заключенное в использовании мультипараллельной архитектуры (GPU), как платформы для реализации и верификации разработанного алгоритма: представленный алгоритм легко “параллелится” на уровне инструкцийс отдельными пикселями (или на “пиксельном уровне”). А значит, каждый поток такой системы в конечном итоге трассирует один из лучей, эмитированных из глаза наблюдателя. Стоит также отметить, что подобный уровень параллелизма инструкций применим к более сложным алгоритмам трассировки лучей (и путей), рассматриваемым в последующих разделах.
Кроме того, на рис. 3 видно одно из самых “проблемных” мест алгоритма с точки зрения его производительности – это поиск пересечения луча и сцены. Подобная схема – без использования ускоряющей структуры – требует проверки пересечения луча с каждым из полигонов сцены, поэтому общая вычислительная сложность алгоритма складывается из сложности теста на пересечение, умноженного на количество полигонов сцены (очевидно, в современных реалиях, где только объекты сцены содержат в себе уже миллионы полигонов, такой подход крайне невыгоден).
Алгоритм трассировки путей по методу Монте Карло
Используя метод Монте Карло для нахождения приближенного значения интеграла из (1), можно получить более непредвзятое и “реалистичное” решение главного уравнения рендеринга (2):
![]() , (3)
, (3)
где направления лучей wi под знаком суммы – равномерно распределены по полусфере с центром в точке p.
Такой подход позволяет достаточно близко аппроксимировать уравнение рендеринга (1) с одним лишь допущением: количество лучей попадающих в конкретную точку ограничено некоторым числом – N. Другими словами, основная идея метода состоит в ограничении бесконечного числа падающих на точку лучей, позволяя, таким образом, трассировать их за “разумное” время.
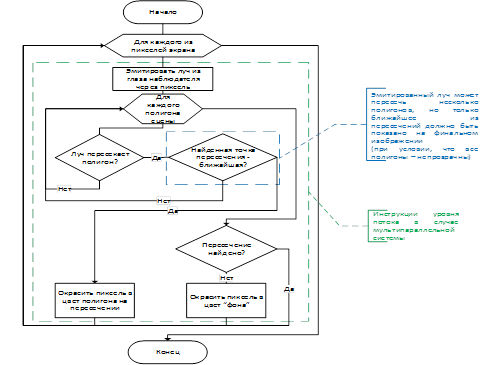
Рисунок 3. Схема простейшего алгоритма рендеринга по методу “бросания лучей”
Метод Монте Карло в решении уравнения рендеринга применяют в алгоритме под названием – “трассировка путей по методу Монте Карло”[2]. Сама по себе трассировка путей также вносит некоторые упрощения в процесс рендеринга. Лучи, подобно методу бросания лучей, испускают из глаза наблюдателя сквозь пиксели в экране. Проходя через них, лучи взаимодействуют с объектами сцены. На каждом их пересечении образуют по одному отраженному и преломленному лучу, до тех пор, пока луч не достигнет источника света. Другими словами, между глазом наблюдателя и источниками света строятся (и трассируются) пути, состоящие из лучей, образованных между пересечениями. Стоит заметить, что сам процесс протекает в “обратном” направлении, нежели в реальной физической модели распространения света. Однако, как было замечено ранее – такой подход не влияет на физику процесса, но позволяет сэкономить на ненужных вычислениях (трассировке) лучей, не попадающих в экран наблюдателя.
Таким образом, можно сказать, что алгоритм трассировки путей, использующий для решения уравнения рендеринга – уравнение (3) с N=1 и называют “алгоритмом трассировки путей по методу Монте Карло”. Его схема представлена на рис. 5.
Видно, что схема алгоритма построена таким образом, что поиск пересечения луча и сцены выделен в отдельную процедуру (сам алгоритм поиска пересечения тот же, что представлен на рис. 3 – в алгоритме по методу “бросания лучей”). Так, процесс разработки алгоритмов ускоряющей структуры затронет лишь эту процедуру, оставив все остальное – без изменений.
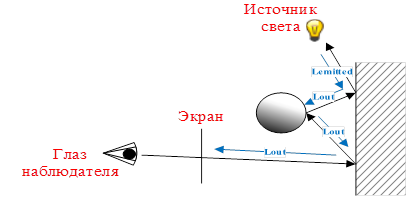
Рисунок 4. Алгоритм трассировки путей
Кроме этого, стоит заметить, что представленная схема показывает операции, выполняемые отдельным потоком (т.е. уже содержит предложенный ранее – “пиксельный уровень” параллелизма). Также, предложенный алгоритм включает в себя рекурсию – для генерации отраженного/преломленного лучей на каждом взаимодействии с объектами сцены. Поскольку генерация лучей завершается, как только путь встречает источник света – количество рекурсивных вызовов в общем случае – не ограничено. Поэтому, для завершения рекурсии используется распространенный в рендеринге метод “русской рулетки” [3]. Идея состоит в том, что исходное уравнение рендеринга (1), а в нашем случае – (3) изменяется таким образом, что в 50% случаев, в качестве решения берется только левое слагаемое (энергия эмиссии света из точки), а в оставшихся – правое (включающее рекурсию). Это вносит некоторую предвзятость в алгоритм, однако позволяет вычислять его за ограниченное время – при помощи “остановки” рекурсии с 50% вероятностью (однако, во время реализации алгоритма не стоит забывать о математической необходимости в этом случае – добавить ½ множители к слагаемым исходного уравнения).
Улучшенный алгоритм трассировки путей по методу Монте Карло
Несмотря на все преимущества стандартного алгоритма трассировки путей по методу Монте Карло, описанного выше, он все еще достаточно сложен для использования в режиме реального времени. Предлагаемая в данном разделе методика позволяет улучшить стандартный алгоритм, сосредоточившись, во-первых – на повышении его производительности (посредством самого алгоритма рендеринга, но не ускоряющей структуры), и во-вторых – на улучшении качества результирующего изображения.
Так, для достижения первой цели, необходимы: генерация отраженных/преломленных лучей с использованием метода выборки по значимости (BRDF importance sampling); поддержка прямого/косвенного освещения.
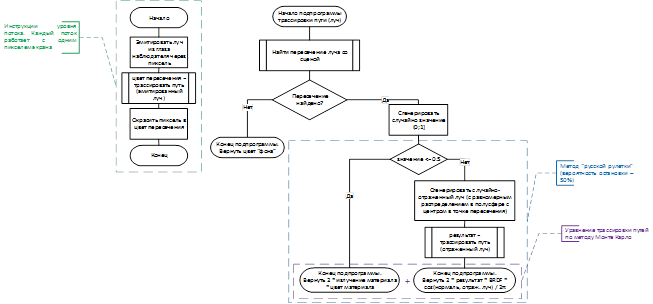
Рисунок 5. Схема алгоритма трассировки путей по методу Монте Карло
Метод выборки по значимости (“BRDF importance sampling”)
Распределение энергии света при отражении от поверхности, вообще говоря, зависит от свойств материала. Это значит, что только “важные” направления вносят вклад в количество энергии света, пришедшей в точку. Например, в случае зеркальной поверхности свет почти полностью отражается в зеркальном направлении, а значит генерировать и трассировать лучи в других направлениях – нет смысла [4,5].

Рисунок 6. Выборка по значимости BRDF
Использование выборки по значимости в методе Монте Карло для решения уравнения рендеринга (3) может быть записано, как:
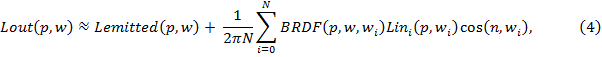
где![]() – функция плотности вероятности, связанная с соответствующей функцией
– функция плотности вероятности, связанная с соответствующей функцией ![]() . Необходимость использования делителя PDF обусловлена фактом генерации отраженного/преломленного луча согласно функции BRDF (в стандартном алгоритме трассировки путей, представленном ранее лучи генерировались равномерно по полусфере, с центром в точке пересечения с объектом сцены – в этом случае коэффициент делитель, очевидно, был равен 2π). Другими словами, неравномерность выборки необходимо корректировать, чтобы интеграл в правой части уравнения (1) аппроксимировался корректно.
. Необходимость использования делителя PDF обусловлена фактом генерации отраженного/преломленного луча согласно функции BRDF (в стандартном алгоритме трассировки путей, представленном ранее лучи генерировались равномерно по полусфере, с центром в точке пересечения с объектом сцены – в этом случае коэффициент делитель, очевидно, был равен 2π). Другими словами, неравномерность выборки необходимо корректировать, чтобы интеграл в правой части уравнения (1) аппроксимировался корректно.
Поддержка прямого/косвенного освещения
Основная идея заключается в рассмотрении всего поступающего в точку света, как состоящего из двух компонент: прямой и косвенной. Первая включает в себя всю энергию, напрямую исходящую от источников света в направлении точки. Вторая же – это отраженные от других объектов лучи.
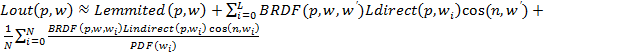 , (5)
, (5)
где:
· ![]() – общее число источников светы сцены;
– общее число источников светы сцены;
· ![]() – включает в себя сумму второго и третьего слагаемых уравнения (без первого –
– включает в себя сумму второго и третьего слагаемых уравнения (без первого – ![]() !), но для “следующей” точки в трассировке пути, которая лежит в направлении
!), но для “следующей” точки в трассировке пути, которая лежит в направлении ![]() относительно точки
относительно точки ![]() . Таким образом, видно, что 3-е слагаемое превращает формулу (5) в рекурсивную.
. Таким образом, видно, что 3-е слагаемое превращает формулу (5) в рекурсивную.
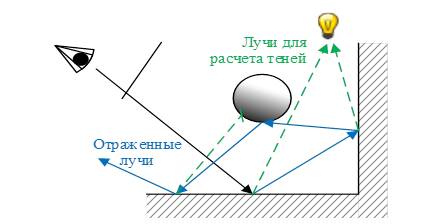
Рисунок 7. Прямое/косвенное освещение
С точки зрения алгоритма такой подход предполагает генерацию 2 типов лучей при взаимодействии (пересечении) с объектом сцены: теневого и отраженного/преломленного. Первый используется для расчета левого слагаемого уравнения (5), второй – преследует те же цели, что и раньше: трассировка пути до источника света, но теперь вносит вклад исключительно косвенной компоненты освещения. Именно поэтому слагаемое Lemitted необходимо исключить из дальнейших расчетов косвенного освещения, о чем говорилось в описании Lindirect.
Заключение
Рассмотрены различные методы решения “главного уравнения рендеринга”, на основе которых разработаны соответствующие алгоритмы рендеринга: простейший алгоритм трассировки по методу “бросания лучей (raycasting)”; стандартная трассировка путей по методу Монте Карло. Кроме того, предложены методики повышения производительности рендеринга (пока без ускоряющей структуры): генерация отраженных/преломленных лучей с использованием выборки по значимости BRDF (BRDF importance sampling); поддержка прямого/косвенного освещения, а также качества результирующего изображения: методика lightsamling для “мягких” теней.
Рецензенты:
Гагарина Л. Г., д.т.н., профессор, заведующий кафедрой «Информатика и программное обеспечение вычислительных систем» Национального исследовательского университета «МИЭТ», г. Москва.
Портнов Е.М., д.т.н., профессор кафедры «Информатика и программное обеспечение вычислительных систем», начальник научно-исследовательской лаборатории «Управляющие информационные системы» Национального исследовательского университета «МИЭТ», г. Москва.
Библиографическая ссылка
Федоров А.Р., Федоров П.А. РАЗРАБОТКА АЛГОРИТМОВ НЕПРЕДВЗЯТОГО 3DРЕНДЕРИНГА // Современные проблемы науки и образования. 2014. № 6. ;URL: https://science-education.ru/ru/article/view?id=15578 (дата обращения: 18.01.2026).



