Как известно, работодатели ожидают от выпускников вуза практических навыков выполнения работ по своей специальности. Для специалистов в информационной сфере деятельности в связи с быстрым развитием информационных технологий эти навыки быстро устаревают. Помочь с этим справиться призвана теоретическая подготовка. Тем не менее, возникает необходимость почти ежегодной корректировки учебных планов в соответствии с потребностями работодателей.
Цель работы – моделирование получаемых студентами теоретических знаний и практических навыков во взаимосвязи с потребностями рынка труда. Для этого применен математический аппарат временных раскрашенных сетей Петри (РСП), наглядно описывающий события в различных дискретных динамических системах, таких как [4], и в том числе при обучении [3].
Разработка математической модели
Смоделируем соотношение качества подготовки специалистов и потребностей рынка рабочей силы помощью РСП (рис. 1). Согласно рабочей документации дисциплины учебного плана формируют свои компетенции, необходимые для профессиональной деятельности (см. стандарт [6]). Номера компетенций обозначим цветом ![]() маркеров сети Петри. Цвета маркеров соответствуют цветам маркеров из [2] с теми же обозначениями позиций, при этом имеется следующее отличие. Школьные знания смоделированы цветом
маркеров сети Петри. Цвета маркеров соответствуют цветам маркеров из [2] с теми же обозначениями позиций, при этом имеется следующее отличие. Школьные знания смоделированы цветом ![]() маркера в позиции
маркера в позиции ![]() , вместо того чтобы использовать несколько позиций PS1, PS2, … PS25 и хранить в каждой вещественное число. Тогда в
, вместо того чтобы использовать несколько позиций PS1, PS2, … PS25 и хранить в каждой вещественное число. Тогда в ![]() маркер имеет цвет
маркер имеет цвет ![]() – вектор вещественных чисел, характеризующих средний уровень знания того или иного школьного предмета. Будем считать, что, так как школьная программа меняется значительно медленнее, чем вузовская,
– вектор вещественных чисел, характеризующих средний уровень знания того или иного школьного предмета. Будем считать, что, так как школьная программа меняется значительно медленнее, чем вузовская, ![]() не меняется. Правила РСП для переходов представлены в табл. 1.
не меняется. Правила РСП для переходов представлены в табл. 1.
Таблица 1
Правила для переходов
|
№ п.п. |
Переход |
Условие
|
Действие
|
|
1. |
|
Сравнивает |
Срабатывает быстро и означает, что специалист компетентен в отношении поступившего поручения и способен его быстро выполнить
|
|
2. |
|
После сравнения
|
Срабатывает долго.
Для |
|
3. |
|
– |
Для
|
Срабатывание перехода ![]() означает, что столько маркеров, сколько студентов в группе (
означает, что столько маркеров, сколько студентов в группе (![]() ), помещается в позицию
), помещается в позицию ![]() , т.е. выпускается группа специалистов. Каждый из этих переходов представляет собой иерархический переход
, т.е. выпускается группа специалистов. Каждый из этих переходов представляет собой иерархический переход ![]() из [2], но могут быть другие дисциплины и семестры изучения. Чем хуже студент что-то выучит, тем меньше будет цвет
из [2], но могут быть другие дисциплины и семестры изучения. Чем хуже студент что-то выучит, тем меньше будет цвет ![]() маркера в позиции
маркера в позиции ![]() , где
, где ![]() – номер соответствующей компетенции.
– номер соответствующей компетенции.
После того, как сработает ![]() , в
, в ![]() появляются
появляются ![]() маркеров. Это означает возможность удовлетворения бывшей группой
маркеров. Это означает возможность удовлетворения бывшей группой ![]() профессиональных требований от работодателей. Атрибуты этих маркеров принимают случайные значения, что соответствует случайным повседневным нуждам. Будем считать, что специалисты трудоустраиваются сразу (а незадолго до и не по истечении длительного времени) после выпуска и по специальности. Тогда пусть атрибуты
профессиональных требований от работодателей. Атрибуты этих маркеров принимают случайные значения, что соответствует случайным повседневным нуждам. Будем считать, что специалисты трудоустраиваются сразу (а незадолго до и не по истечении длительного времени) после выпуска и по специальности. Тогда пусть атрибуты ![]() соответствующих маркеров в
соответствующих маркеров в ![]() приобретают какие-либо из значений атрибутов
приобретают какие-либо из значений атрибутов ![]() маркеров в позиции
маркеров в позиции ![]() .
.
Один случайно выбранный маркер в ![]() обозначим как
обозначим как ![]() . Он представляет компетенции одного выпускника. В [2] введен ряд числовых констант
. Он представляет компетенции одного выпускника. В [2] введен ряд числовых констант ![]() . Если результаты сравнения (см. п. 1 табл. 1) на удовлетворительном уровне
. Если результаты сравнения (см. п. 1 табл. 1) на удовлетворительном уровне ![]() , то
, то ![]() срабатывает быстро. Если запрос не включает ни одну компетенцию, то сравнение производится по области знаний (из некоторого стандартного классификатора).
срабатывает быстро. Если запрос не включает ни одну компетенцию, то сравнение производится по области знаний (из некоторого стандартного классификатора).
Рассмотрим п. 2 табл. 1. Если результат сравнения неудовлетворительный, то срабатывает ![]() . Это означает обращение к тем или иным внешним источникам информации либо проведение собственных микроисследований. Время срабатывания
. Это означает обращение к тем или иным внешним источникам информации либо проведение собственных микроисследований. Время срабатывания ![]() больше, чем для
больше, чем для ![]() . При этом освежаются старые знания, в связи с чем в [2] введена константа
. При этом освежаются старые знания, в связи с чем в [2] введена константа ![]() , например,
, например, ![]() . Возможно приобретение совершенно нового опыта, для этого в [2] введена константа
. Возможно приобретение совершенно нового опыта, для этого в [2] введена константа ![]() , например,
, например, ![]() . Она меньше единицы, потому что для надлежащего запоминания требуется повторение. Знания со временем забываются [7]. Чтобы это учесть, в [2] введена константа забывания, например,
. Она меньше единицы, потому что для надлежащего запоминания требуется повторение. Знания со временем забываются [7]. Чтобы это учесть, в [2] введена константа забывания, например, ![]() . Если знания забыты или устарели, они обновляются с помощью
. Если знания забыты или устарели, они обновляются с помощью ![]() , причем снова не до единицы, а с использованием константы
, причем снова не до единицы, а с использованием константы ![]() , например,
, например, ![]() .
.
Средняя производительность сети Петри оценивает аналогичную величину для реальных специалистов. Чтобы производительность выпускников тотчас после выпуска была на высоком уровне, надо удовлетворить ряд условий, которые требуются для обучения – хорошие расписание, учебный план, материальная база, преподаватели. Например, для составления расписания разработан комплекс программ, использующий наиболее эффективный алгоритм из [1].
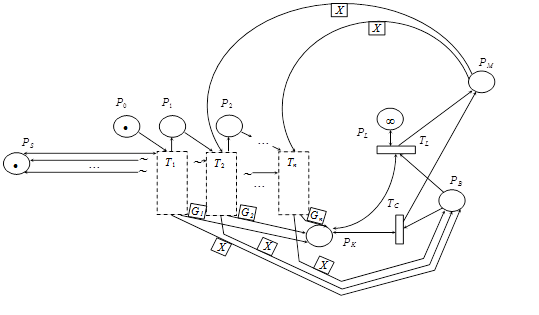
Рис.1. Модель непрерывной подготовки специалистов
Символ ~ означает воображаемой продолжение линии, огибающее препятствие
![]() – иерархические переходы (потоки обучения);
– иерархические переходы (потоки обучения);
![]() ,
, ![]() – кратности дуг;
– кратности дуг;
![]() – позиция с информацией о качестве работы выпускников;
– позиция с информацией о качестве работы выпускников;
![]() – переход, означающий компетентность специалиста;
– переход, означающий компетентность специалиста;
![]() – переход, означающий обращение в библиотеку или Интернет;
– переход, означающий обращение в библиотеку или Интернет;
![]() – позиция для хранения профессиональных запросов;
– позиция для хранения профессиональных запросов;
![]() – позиция, моделирующая выпущенных специалистов;
– позиция, моделирующая выпущенных специалистов;
![]() – позиция, моделирующая школьные знания;
– позиция, моделирующая школьные знания;
![]() – позиции, задающие последовательности приема на 1 курс.
– позиции, задающие последовательности приема на 1 курс.
По мере обучения студентов на старших курсах на первый курс поступают новые. У них могут быть другие учебные планы. То есть на факультете одновременно обучаются разные курсы. В сети имеется ![]() переходов
переходов ![]() , каждый из которых соответствует своему потоку обучения (со своим годом приема и учебным планом, по порядку индексов в обозначениях). Последовательность их возбуждения определяется маркировкой позиций
, каждый из которых соответствует своему потоку обучения (со своим годом приема и учебным планом, по порядку индексов в обозначениях). Последовательность их возбуждения определяется маркировкой позиций ![]() . Т.е. исходя из рисунка видно, что первым возбужден
. Т.е. исходя из рисунка видно, что первым возбужден ![]() , затем будет
, затем будет ![]() , и т.д.
, и т.д.
После возбуждения они, казалось бы, должны работать длительное время, соответственно периоду обучения студентов. Но чтобы не отступать от классических сетей Петри, где срабатывает одновременно только один переход, будем полагать, что это не так. Результат работы сети от этого не меняется. ![]() – кратности дуг, т.е. количества выпускников.
– кратности дуг, т.е. количества выпускников.
Одной из целей данного рисунка является показ наличия обратной связи в социальной системе «вуз-работодатели». Позиция ![]() означает накопление обществом информации о качестве работы выпускников. Когда очередные
означает накопление обществом информации о качестве работы выпускников. Когда очередные ![]() поручений работодателей будут выполнены, там будет
поручений работодателей будут выполнены, там будет ![]() маркеров с различным значением атрибутов
маркеров с различным значением атрибутов ![]() времени обработки запроса. Потом, используя кратные дуги, все эти атрибуты обрабатываются очередным переходом
времени обработки запроса. Потом, используя кратные дуги, все эти атрибуты обрабатываются очередным переходом ![]() , т.е. от них зависит
, т.е. от них зависит ![]() .
. ![]() связано с эффективностью работы специалистов, определяемой работодателями и формирующей то или иное общественное мнение, принимаемое к сведению руководством вуза. Последнее может выплачивать премии преподавателям, делать поручения обновлять оборудование или ремонтировать аудитории в числе факторов, ведущих к успешному обучению.
связано с эффективностью работы специалистов, определяемой работодателями и формирующей то или иное общественное мнение, принимаемое к сведению руководством вуза. Последнее может выплачивать премии преподавателям, делать поручения обновлять оборудование или ремонтировать аудитории в числе факторов, ведущих к успешному обучению.
В связи с тем, что каждый выпуск добавляет разных специалистов с разными компетенциями, в позиции ![]() будет все больше и больше маркеров. Выбор среди них для сравнения цветов маркеров производится случайным образом. Большее число специалистов означает, что они могут справиться с большим числом поручений, но если
будет все больше и больше маркеров. Выбор среди них для сравнения цветов маркеров производится случайным образом. Большее число специалистов означает, что они могут справиться с большим числом поручений, но если ![]() велико, среднее время обработки сильно не изменится. При генерации значений мест трудоустройства следует ограничивать их общее число небольшим значением, например, 20.
велико, среднее время обработки сильно не изменится. При генерации значений мест трудоустройства следует ограничивать их общее число небольшим значением, например, 20.
Обычно специалист делает одно и то же, привыкает и делает это быстро. Лишь изредка приходится изучать что-то новое или восстанавливать в памяти забытое. Тут имеется сходство с кэшированием в операционных системах. Известно, что в не менее 90% случаев обращение в компьютере происходит к тем адресам оперативной памяти, содержимое которых продублировано в быстродействующем кэше [5]. Компетенции выпускника соответствуют содержимому кэш-памяти. Что он не знает, или редко использует и забыл, вынужден где-то искать, по аналогии с более медленной основной памятью. Основополагающий принцип кэширования - локальность данных во времени – переносится на приведенную модель следующим образом. Если босс недавно поручил что-то сделать, то вероятно, он вскоре поручит делать что-то похожее. Поэтому надо запоминать, что и как делали.
В связи с существованием развитой теории кэширования [5] рассмотрим ее применение для данной модели. Второй основополагающий принцип кэширования – пространственная локальность данных и исполняемого кода, т.е. если было обращение по некоторому адресу, высока вероятность, что скоро потребуется обращение по близлежащему адресу. Значит, если босс что-то требует от подчиненного, возможно, что вскоре он потребует чего-то связанного с первым, но которое выполняется по-другому. Если узкий специалист занимается только своим делом, то делает он его быстро, а хоть и есть дела, связанные с первым, ими должны заниматься другие сотрудники. Самих дел обычно не так много, как адресов в памяти ЭВМ, и в общих чертах можно было бы научиться, как их выполнять, но это затратно, и мало кто на это пойдет. Ради справедливости отметим, что и временные задержки здесь отличаются не на микросекунды, как в ЭВМ, а могут измеряться часами.
Кэширование бывает многоуровневое. Первый уровень соответствует тому, что специалист очень хорошо знает и выполняет, например, еженедельно или ежемесячно. Если нечто требуется выполнять реже, специалист успевает подзабыть, но все же он знает, где находится справочная информация и как быстро ее извлечь, это соответствует второму уровню кэша. Новые поручения приходится обдумывать, как выполнить. Специалист может спросить у коллег, но и они могут не знать или из-за недостатка времени не говорить. Тогда к его услугам сеть Интернет, если к ней имеется доступ. Это как бы кэш последнего уровня, после которого необходимы уже радикальные меры для получения информации. Например, можно пойти в библиотеку, или работать методом проб и ошибок, что соответствует обращению к основной памяти ЭВМ.
Существует два основных алгоритма кэширования – сквозной и обратной записи. Имеется в виду, что кэшируется не только чтение, но и запись. Однако, соответственно, большинство специалистов не являются исследователями и новую методику работы обычно не создают, поэтому необходимости в ее запоминании, как правило, нет.
Кэш бывает случайный, когда адреса в нем для кэширования выбираются случайно, и детерминированный, когда эти адреса привязаны к наборам адресов внешней памяти, а также возможна их комбинация. Для специалистов это означает только способ организации ими справочной информации на каких-либо носителях – записных книжках, каталогах файлов и т.п. Например, бывают записные книжки с алфавитными закладками страниц, что эффективно, но со временем они заполняются, теряются, изнашиваются, а также снижается конфиденциальность.
Данные из кэша после его заполнения вытесняются новыми данными, для этого применяются различные алгоритмы замещения страниц, такие как рабочего набора и др. В практике специалистов это применяется в том виде, что время от времени можно выбрасывать устаревшие справочники, старые блокноты, или чистить флэш-накопители. Однако ни о каких алгоритмах для систематизации этих действий не может быть и речи.
Между понятиями «кэширование» и «моделирование» также имеется связь. Моделирование, в том числе математическое, означает работу с моделью, лишенной несущественных свойств объекта моделирования для удешевления эксперимента, например по времени. Кэширование означает сохранение лишь самых актуальных значений из оперативной памяти для ускорения доступа. Это снижает энергопотребление и время, проведенное за компьютером. То есть, как то, так и другое можно направить на облегчение какой-либо работы. Так, представленная на рис. 1 математическая модель абстрагирована от воспитательной и научной работы, проводимой со студентами. Она не учитывает всех тонкостей учебного плана – его дисциплин, сроков их изучения, форм контроля. Но зато ее значительно легче запрограммировать, чтобы провести вычислительный эксперимент.
Заключение
Достоинством используемой РСП является то, что хотя она и использует известные расширения классических сетей, но не требует применения ингибиторных дуг, а это упрощает логику. Модель является расширением модели [2] для учета обучения на нескольких курсах одновременно. Некоторые из принципов кэширования находят свое применение в повседневной жизни выпускников. Это наиболее характерно для принципа временной локальности, что и нашло отражение в предложенной модели. Для модели кэширования [3, С. 55] проведен вычислительный эксперимент, показывающий соответствие результатов ожидаемым числовым значениям согласно [5].
Рецензенты:
Белов В.В., д.т.н., профессор, декан инженерного факультета ФГБОУ ВПО «Чувашская государственная сельскохозяйственная академия», г. Чебоксары;
Захаров В.М., д.т.н., профессор кафедры компьютерных систем Казанского национального исследовательского технического университета им. А.Н. Туполева (КАИ), г. Казань.
Библиографическая ссылка
Димитриев А.П. МОДЕЛИРОВАНИЕ ПРИМЕНЕНИЯ ЗНАНИЙ СПЕЦИАЛИСТОВ РАСКРАШЕННЫМИ СЕТЯМИ ПЕТРИ // Современные проблемы науки и образования. 2014. № 6. ;URL: https://science-education.ru/ru/article/view?id=15518 (дата обращения: 03.07.2025).



