В прикладных задачах, как правило, изучается не сам граф, а процессы на нём. Большинство из них связано с перемещениями по путям на графе. В классическом определении путь – это последовательность дуг графа, в которой каждая следующая дуга начинается в вершине, в которой заканчивается предыдущая дуга. Соединимость одной вершины путём, ведущим из другой вершины, называется достижимостью одной вершины из другой. Три основных задачи прикладной (алгоритмической) теории графов связаны с достижимостью. Это сама задача о достижимости и нахождении кратчайшего пути, задача о случайных блужданиях по вершинам графа и задачи о потоках в сетях, поскольку поток можно считать перемещением (транспортировкой) «вещества» (информации, материи, товаров, жидкости, энергии и т.п.) из источника в сток по путям, ведущим из источника в сток.
Когда мы говорим о графе с ограничением на достижимость, это означает, что допустимыми на нём являются не все пути, а только пути, удовлетворяющие определенному условию (это условие называется типом или видом ограничений на достижимость). Как правило, тип достижимости возникает после того, как задано некоторое разбиение множества дуг графа, а ограничения на достижимость формулируются с помощью (в терминах) этого разбиения.
Характерной особенностью задач на графах с ограничениями на достижимость является неприменимость напрямую классических алгоритмов, поскольку они предполагают, что все возможные пути на графе являются допустимыми.
Графы с нестандартной достижимостью – первый известный пример, когда мультиграфы (графы с кратными дугами) приходится рассматривать по существу, т.е. когда задача, исходно поставленная на мультиграфе, не может быть сведена к задаче на обычном графе заменой кратных дуг кратчайшей из них в задаче о кратчайших путях или дугой с суммарной пропускной способностью в потоковых задачах. Это связано с тем, что кратные дуги могут быть разных типов.
Изучение графов с ограничениями на достижимость (далее – нестандартная достижимость) началось сравнительно недавно. Первые работы в этой области принадлежат Я.М. Ерусалимскому и Е.О. Басанговой ([1],[3]), следующие результаты принадлежат Я.М. Ерусалимскому, А.В. Скороходову, А.Г. Петросяну, М.В. Кузьминовой и Н.Н. Водолазову ([3]–[5]). В этих работах были определены и изучены различные типы нестандартной достижимости, в частности: смешанная, магнитная, вентильная, барьерная. Все эти типы ограничений формулировались в виде некоторых требований, предъявляемых к последовательности дуг, допустимых этим типом достижимости путей.
В прикладных задачах ограничения могут возникать не только на порядок прохождения по дугам графа, но и на порядок прохождения по его вершинам. Рассмотрение ограничений такого вида естественно и с общенаучной точки зрения, поскольку делает завершенным круг рассматриваемых ограничений. Это естественно и по той причине, что путь на графе часто определяют как последовательность вершин графа ![]() , в которой каждая пара вершин
, в которой каждая пара вершин ![]() соединена дугой в направлении от первой вершины ко второй.
соединена дугой в направлении от первой вершины ко второй.
Ниже мы определим различные виды нестандартной достижимости, определяемые в терминах последовательности вершин пути. Будет показано, что каждый из введенных типов вершинной нестандартной достижимости сводится к соответствующему типу достижимости, определенному в терминах дуг графа (т.е. с определением пути как последовательности дуг). Тем самым результаты, полученные ранее (см. [5]), переносятся на графы с вершинной нестандартной достижимостью.
1. Вершинная смешанная достижимость порядка k
Определение 0.1. Ориентированным графом называют тройку ![]() , где
, где ![]() – множество вершин графа,
– множество вершин графа, ![]() – множество дуг графа,
– множество дуг графа, ![]() – отображение смежности (инцидентности).
– отображение смежности (инцидентности).
Определение 1.1. ▼ Пусть ![]() – орграф. Множество вершин графа
– орграф. Множество вершин графа ![]() . Вершинно-смешанным путем порядка k (
. Вершинно-смешанным путем порядка k (![]() ) на графе будем называть путь, на котором вершины из множества
) на графе будем называть путь, на котором вершины из множества ![]() встречаются не более чем k раз подряд. ▲
встречаются не более чем k раз подряд. ▲
Вершины множества ![]() будем называть нейтральными, а множества
будем называть нейтральными, а множества ![]() – запрещенными.
– запрещенными.
Определение 1.2. Графом с вершинной смешанной достижимостью порядка k будем называть граф, на котором допустимыми являются только смешанные пути порядка k.
Пример 1.1. ▼ На рис. 1.1. изображен граф с вершинной смешанной достижимостью порядка 3. Черная заливка – запрещенные вершины, серая – разрешенные вершины.
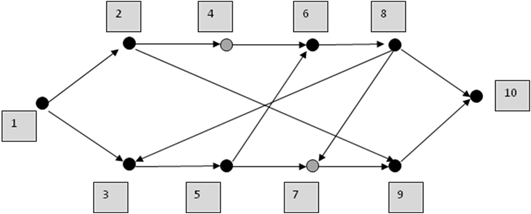
Рис. 1.1.
На этом графе пути 1– 2–4–6–8– 10, 1–3–5– 7–9–10, 1–2–9–10, 1–2–4–6–8–3–5–7–9–10 запрещенные, а разрешенным путем из вершины 1 в вершину 10 является только один путь 1– 2–4–6–8–7–9–10.▲
Со случаем, когда k=2 все обстоит очень просто, нужно из графа удалить дуги, обе граничные вершины которых находятся во множестве ![]() , и рассматривать обычную достижимость на полученном графе.
, и рассматривать обычную достижимость на полученном графе.
В случае, когда ![]() , задача о вершинной смешанной достижимостью порядка k сводится к задаче о смешанной достижимости порядка
, задача о вершинной смешанной достижимостью порядка k сводится к задаче о смешанной достижимости порядка ![]() на дугах. Для этого во множество
на дугах. Для этого во множество ![]() нужно включить все дуги исходного графа, обе граничные вершины которых находятся во множестве
нужно включить все дуги исходного графа, обе граничные вершины которых находятся во множестве ![]() , и положить
, и положить ![]() .
.
После такого перехода можно согласно [5] построить развёртку исходного графа – вспомогательный граф, позволяющий решать задачи о кратчайших путях, случайных блужданиях и потоках на развертке, а их решения интерпретировать как решение соответствующей задачи на исходном графе с ограничением на достижимость.
2. Вершинная барьерная достижимость высоты h
Пусть ![]() - граф,
- граф, ![]() , множества
, множества ![]() ,
, ![]() и
и ![]() попарно не пересекаются. Множество
попарно не пересекаются. Множество ![]() – множество нейтральных вершин,
– множество нейтральных вершин, ![]() – множеством вершин, увеличивающих барьерный показатель (множество увеличивающих вершин),
– множеством вершин, увеличивающих барьерный показатель (множество увеличивающих вершин), ![]() – множество барьерных вершин.
– множество барьерных вершин.
Определение 1.3. ▲ С каждым отрезком ![]() (где
(где ![]() ) пути
) пути ![]() свяжем числовую характеристику
свяжем числовую характеристику ![]() , определенную индуктивно следующим:
, определенную индуктивно следующим:
1. 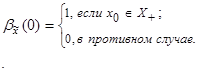
2. 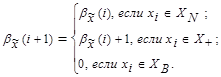
Характеристика![]()
![]() называется величиной накопленной энергии на отрезке
называется величиной накопленной энергии на отрезке ![]() пути
пути ![]() .▼
.▼
Определение 1.4. ▼ Графом с барьерной достижимостью высоты ![]() будем называть граф
будем называть граф ![]() , все пути
, все пути ![]() , на котором удовлетворяют условию:
, на котором удовлетворяют условию:
![]() . ▲ (1.2)
. ▲ (1.2)
Другими словами, если к ![]() -му шагу путь
-му шагу путь ![]() от своего начала накопил величину барьерного показателя
от своего начала накопил величину барьерного показателя ![]() большую либо равную
большую либо равную ![]() , то на последующем шаге становятся допустимыми для прохождения вершины из множества
, то на последующем шаге становятся допустимыми для прохождения вершины из множества ![]() .
.
Пример 1.2. ▼ Рассмотрим граф, изображенный на рис 4.11 с барьерной вершинной достижимостью порядка 2. Черная заливка – барьерные вершины, серая – увеличивающие вершины, без заливки – нейтральные вершины.
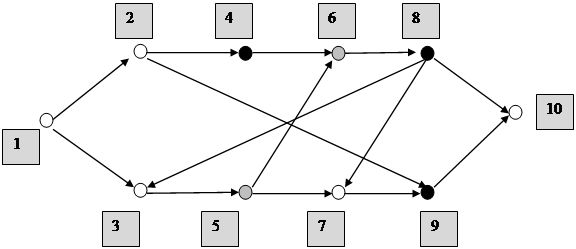
Рис. 1.2.
На этом графе пути 1– 2–4–6–8– 10, 1–3–5– 7–9–10, 1–2–9–10 запрещенные, а разрешенным путем из вершины 1 в вершину 10 является путь 1–3–5–6–8– 10▲
Как задачу о вершинной барьерной достижимости высоты h свести к барьерной достижимости высоты h (см. [5]), определенной на дугах графа?
Ясно, что нужно положить
![]() ;
; ![]() ,
, ![]()
и рассмотреть барьерную достижимость (на дугах графа) высоты h при определенном нами разбиении множества дуг графа.
После такого перехода можно построить развёртку исходного графа (см. [5]) – вспомогательный граф, позволяющий решать задачи о кратчайших путях, случайных блужданиях и потоках на развертке, а их решения интерпретировать как решение соответствующей задачи на исходном графе с вершинной барьерной достижимостью.
3. Возможные приложения смешанной достижимости
Рассмотрим описание технологического процесса в виде графа, вершины которого соответствуют различным состояниям изделия, в котором оно может находиться в процессе изготовления. Дуги графа соответствуют выполняемым операциям, переводящим изделие из одного состояния в другое.
Граф технологического процесса в этом случае представляет собой классическую сеть с одним входом (источником) и одним выходом (стоком).
Если под длиной дуги, ведущей из вершины x в вершину y, понимать стоимость выполнения операции, переводящей изделие из состояния x в состояние y, то мы получаем задачу поиска оптимального по стоимости пути выполнения технологического процесса.
Для многих технологических процессов имеют место дополнительные ограничения на возможные пути на графе технологического процесса. Например, при выполнении операции изделие может нагреваться, и если такие операции выполняются непосредственно одна за другой, то возможен перегрев изделия и его выход из строя в процессе изготовления.
Отнесение дуг, соответствующих таким операциям, ко множеству![]()
![]() , а остальных дуг ко множеству
, а остальных дуг ко множеству ![]() и рассмотрение графа технологического процесса как графа со смешанной достижимостью порядка k позволяет найти оптимальный по стоимости путь исполнения процесса с учетом технологических ограничений.
и рассмотрение графа технологического процесса как графа со смешанной достижимостью порядка k позволяет найти оптимальный по стоимости путь исполнения процесса с учетом технологических ограничений.
Выводы
Определенные в работе типы ограничений на достижимость расширяют класс возможных приложений графов и алгоритмов на графах, в том числе для описания и оптимизации информационных и технологических процессов.
Рецензенты:
Наседкин А.В., д.ф.-м.н., профессор, профессор кафедры математического моделирования, Южный федеральный университет, г. Ростов-на-Дону;
Белявский Г.И., д.т.н., профессор, заведующий кафедрой исследования операций и высшей математики, Южный федеральный университет, г. Ростов-на-Дону.
Библиографическая ссылка
Ерусалимский Я.М. ГРАФЫ С ОГРАНИЧЕНИЯМИ НА ДОСТИЖИМОСТЬ И ИХ ПРИЛОЖЕНИЕ К ЗАДАЧАМ ОПТИМИЗАЦИИ ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ // Современные проблемы науки и образования. – 2014. – № 6. ;URL: https://science-education.ru/ru/article/view?id=15477 (дата обращения: 27.04.2024).



