Абсорбция газов является экзотермическим процессом. Но в большинстве известных в настоящее время теоретических методов расчета процесса абсорбции используется приближение изотермического процесса, а сопутствующими процессами выделения и переноса тепла пренебрегают. Некоторые авторы [8,9] указывают на то, что тепловым эффектам при абсорбции газов уделяется недостаточно внимания.
В статье предлагается метод расчета кинетики неизотермической абсорбции, в котором наиболее полно учитывается влияние тепловых эффектов на процесс массопередачи при абсорбции. Уравнения тепло- и массопередачи получены в рамках нелокальной версии термодинамики, разработанной Майковым В.П. (НВТ) [3,4]. Этот подход позволяет описать процессы переноса тепла и массы без постулирования каких-либо модельно-механизменных представлений, а полученные выводы в значительной степени сохраняют термодинамический характер.
В работе [5] кратко изложены основы нелокальной версии термодинамики, получено выражение для равновесного потока массы
![]() . (1)
. (1)
где ![]() – скорость звука в данной среде, м/с;
– скорость звука в данной среде, м/с;
![]() – молярная плотность смеси, кмоль/м3;
– молярная плотность смеси, кмоль/м3;
![]() – мольная доля компонента.
– мольная доля компонента.
Для равновесного теплового потока в рамках той же теории можно получить следующее выражение
![]() , (2)
, (2)
где ![]() - массовая плотность смеси,
- массовая плотность смеси, ![]() .
.
Если подставить значения скорости звука и плотности ![]() ,
, ![]() смеси для идеально газовых условий в уравнения (1) и (2), то можно получить следующие выражения для равновесных потоков массы и тепла
смеси для идеально газовых условий в уравнения (1) и (2), то можно получить следующие выражения для равновесных потоков массы и тепла
![]() , (3)
, (3)
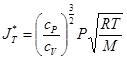 . (4)
. (4)
Интересно сравнить эти зависимости с идеальным потоком частиц и удельным потоком энергии, полученным в рамках статистической физики [6,с. 110, с. 472].
![]() , (5)
, (5)
![]() . (6)
. (6)
Выражения для ![]() и
и ![]() и для
и для ![]() и
и ![]() совпадают с точность до постоянного множителя, что подтверждает правильность выбора характерного линейного размера.
совпадают с точность до постоянного множителя, что подтверждает правильность выбора характерного линейного размера.
Перейдем непосредственно к описанию процесса переноса тепла и массы из одной фазы в другую. При совместном тепломассопереносе через одну и ту же поверхность принято считать[1,2,7], что перепад температур и концентраций в основном происходит в тонком слое, прилегающем к границе раздела фаз. Для описания неравновесных процессов, протекающих в приграничном ламинарном слое, как правило, можно применить линейное приближение. Тогда результирующая неравновесная плотность потока массы в линейном приближении для неизотермических условий запишется так
![]() (7)
(7)
Оценим величину перепада концентраций ![]() и температур
и температур ![]() . Если во всем ламинарном слое толщиной
. Если во всем ламинарном слое толщиной ![]() наблюдается перепад концентраций
наблюдается перепад концентраций ![]() и перепад температур
и перепад температур ![]() (где
(где ![]() и
и ![]() - равновесные значения концентраций и температур на границе раздела фаз), а элементарный перепад концентраций
- равновесные значения концентраций и температур на границе раздела фаз), а элементарный перепад концентраций ![]() и температур
и температур ![]() осуществляется на длине, равной характерному радиусу взаимодействия
осуществляется на длине, равной характерному радиусу взаимодействия ![]() (см. рис. 1), то величины элементарных перепадов могут быть оценены следующим образом
(см. рис. 1), то величины элементарных перепадов могут быть оценены следующим образом
![]() , (8)
, (8)
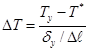 . (9)
. (9)
Подставляя выражения равновесного мольного потока (1) в (7) и учитывая (8) и (9) получим уравнение для неравновесного мольного потока в неизотермических условиях
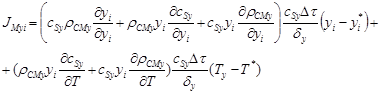 (10)
(10)
Представим мольный поток в виде произведения плотности потока на некоторую скорость переноса, которую будем называть скоростью переноса субстанции
![]() , (11)
, (11)
где ![]() , (12)
, (12)
![]() , (13)
, (13)
![]() . (14)
. (14)
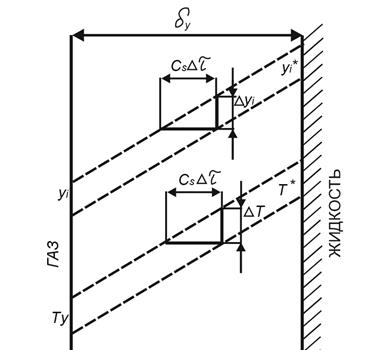
Рис.1. Условия на межфазной границе.
Вместо скорости переноса субстанции ![]() удобно ввести безразмерную характеристику процесса переноса массы – коэффициент переноса
удобно ввести безразмерную характеристику процесса переноса массы – коэффициент переноса![]() , который определяется выражением
, который определяется выражением
![]() . (15)
. (15)
Тогда величина неравновесного мольного потока со стороны газовой фазы окончательно запишется следующим образом
![]() . (16)
. (16)
Рассуждая аналогичным образом можно получить выражение для потока массы от границы раздела фаз в ядро жидкой фазы.
Для полного описания процессов тепломассопереноса необходимо составить уравнение теплового баланса. При этом важно учесть все виды тепловых эффектов газовой абсорбции. Обычно выделяют следующие виды тепловых эффектов [1,2,7] : 1- повышение температуры жидкости за счет тепла абсорбции; 2- понижение температуры жидкости за счет испарения растворителя; 3- теплопередача между контактирующими фазами; 4- теплопередача между материальными потоками и стенками аппарата (тепловые потери).
В дальнейших рассуждениях будем рассматривать случай адиабатической абсорбции (тепловыми потерями пренебрегаем). Получим на основе нелокальной версии термодинамики уравнение для расчета теплопередачи между фазами. Ранее (см. формулу (2)) было получено уравнение для расчета теплового потока в равновесных условиях. Чтобы получить неравновесный тепловой поток, снова воспользуемся линейным приближением и запишем
![]() . (17)
. (17)
Величина ![]() - это элементарный перепад температур, который определяется уравнением (19). После дифференцирования равновесного теплового потока (2) и подстановки уравнения (9) в (17) получим
- это элементарный перепад температур, который определяется уравнением (19). После дифференцирования равновесного теплового потока (2) и подстановки уравнения (9) в (17) получим
![]() . (18)
. (18)
Представим тепловой поток в виде произведения скорости переноса субстанции на плотность теплового потока
![]() . (19)
. (19)
Где скорость переноса субстанции ![]() определяется выражением (12). Вводя безразмерный коэффициент переноса
определяется выражением (12). Вводя безразмерный коэффициент переноса ![]() по уравнению (15), запишем выражение для неравновесного теплового потока со стороны газовой фазы
по уравнению (15), запишем выражение для неравновесного теплового потока со стороны газовой фазы
![]() , (20)
, (20)
где ![]() , (21)
, (21)
![]() . (22)
. (22)
Здесь ![]() - коэффициент теплоотдачи в газовой фазе,
- коэффициент теплоотдачи в газовой фазе, ![]() . Путем аналогичных рассуждений можно получить уравнение для неравновесного теплового потока в жидкой фазе.
. Путем аналогичных рассуждений можно получить уравнение для неравновесного теплового потока в жидкой фазе.
Рассмотрим тепловые эффекты газовой абсорбции. Обычно принимают, что тепло при растворении газа выделяется на границе раздела фаз (аналогично – при испарении растворителя охлаждается граница раздела фаз). Примем эту гипотезу в качестве рабочей. Тогда уравнение теплового баланса для выделенного объема на границе раздела фаз запишется в виде
![]() (23)
(23)
где ![]() - поток тепла от ядра газовой фазы к границе раздела фаз,
- поток тепла от ядра газовой фазы к границе раздела фаз, ![]() ;
;
![]() - поток тепла от границы раздела фаз в ядро жидкой фазы,
- поток тепла от границы раздела фаз в ядро жидкой фазы, ![]() ;
;
![]() - теплота абсорбции,
- теплота абсорбции, ![]() ;
;
![]() - теплота испарения растворителя,
- теплота испарения растворителя, ![]() .
.
Теплота абсорбции ![]() и теплота испарения растворителя
и теплота испарения растворителя ![]() определяются следующим образом
определяются следующим образом
![]() , (24)
, (24)
![]() , (25)
, (25)
где ![]() - удельная теплота абсорбции i-го компонента,
- удельная теплота абсорбции i-го компонента, ![]() ;
;
![]() - удельная теплота испарения растворителя,
- удельная теплота испарения растворителя, ![]() ;
;
![]() - удельный мольный поток растворителя,
- удельный мольный поток растворителя, ![]() .
.
Уравнение массоотдачи в газовой фазе (16), аналогичное ему выражение для неравновесного мольного потока в жидкой фазе, условие фазового равновесия
![]() , (26)
, (26)
где ![]() - константа фазового равновесия для i-го компонента; уравнения теплоотдачи для газовой (20) и жидкой фаз образуют исходную систему уравнений для описания процессов тепломассообмена при неизотермической абсорбции. Решая эту систему относительно неизвестных
- константа фазового равновесия для i-го компонента; уравнения теплоотдачи для газовой (20) и жидкой фаз образуют исходную систему уравнений для описания процессов тепломассообмена при неизотермической абсорбции. Решая эту систему относительно неизвестных ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , получим:
, получим:
- уравнение массопередачи для неизотермических условий
![]() , (27)
, (27)
где ![]() ,
,
![]() ,
,
![]() ,
,
![]()
где ![]() - коэффициент массопередачи i-го компонента,
- коэффициент массопередачи i-го компонента, ![]() ;
;
![]() - коэффициенты массоотдачи,
- коэффициенты массоотдачи, ![]() ,
,
- уравнение теплопередачи
![]() (28)
(28)
(тепловой поток в жидкой фазе определяется из балансового соотношения (23)),
и уравнение для расчета равновесной температуры на границе раздела фаз
![]()
Величины ![]() , входящие в уравнение для коэффициента массоотдачи, а также величины
, входящие в уравнение для коэффициента массоотдачи, а также величины ![]() (
(![]() ), входящие в уравнение для коэффициента теплоотдачи, рассчитываются теоретически. Они зависят от физических свойств смеси - скорости звука, плотности, молекулярной массы. Безразмерный коэффициент переноса субстанции
), входящие в уравнение для коэффициента теплоотдачи, рассчитываются теоретически. Они зависят от физических свойств смеси - скорости звука, плотности, молекулярной массы. Безразмерный коэффициент переноса субстанции ![]() характеризует гидродинамические условия, в которых протекают процессы тепло- и массопередачи и теоретически не может быть определен в рамках поставленной в статье задачи. В общем случае коэффициент переноса
характеризует гидродинамические условия, в которых протекают процессы тепло- и массопередачи и теоретически не может быть определен в рамках поставленной в статье задачи. В общем случае коэффициент переноса ![]() меньше единицы. В пределе он может быть равным единице и тогда
меньше единицы. В пределе он может быть равным единице и тогда ![]() , а
, а ![]() , то есть процесс переноса массы и тепла будет происходить с максимально возможной скоростью, равной скорости звука в данной среде, а толщина пограничного ламинарного слоя
, то есть процесс переноса массы и тепла будет происходить с максимально возможной скоростью, равной скорости звука в данной среде, а толщина пограничного ламинарного слоя![]() будет равна характерному линейному размеру
будет равна характерному линейному размеру ![]() .
.
При использовании уравнения массопередачи (27) и уравнения теплопередачи (28) для расчета тепломассообменного процесса коэффициентами переноса ![]() и
и ![]() необходимо задаваться и корректировать их в зависимости от того, какое распределение концентраций по высоте аппарата необходимо получить. Поэтому задача расчета неизотермического абсорбера ставится в поверочном варианте. Алгоритм расчета по предложенной модели и результаты расчета однокомпонентной и многокомпонентной изотермической абсорбции будут изложены в следующем сообщении.
необходимо задаваться и корректировать их в зависимости от того, какое распределение концентраций по высоте аппарата необходимо получить. Поэтому задача расчета неизотермического абсорбера ставится в поверочном варианте. Алгоритм расчета по предложенной модели и результаты расчета однокомпонентной и многокомпонентной изотермической абсорбции будут изложены в следующем сообщении.
Рецензенты:
Богомолов А.Н., д.т.н., профессор, проректор по научной работе ФГБОУ ВПО «Волгоградский государственный архитектурно-строительный университет» , г. Волгоград;
Семенов Б.А., д.т.н., профессор, заведующий кафедрой «Промышленная теплотехника» ФГБОУ ВПО «Саратовский государственный технический университет им. Ю.А. Гагарина», г. Саратов.
Библиографическая ссылка
Неумоина Н.Г., Белов А.В. ПОСТРОЕНИЕ МОДЕЛИ КИНЕТИЧЕСКОГО МЕТОДА РАСЧЕТА МНОГОКОМПОНЕНТНОЙ НЕИЗОТЕРМИЧЕСКОЙ АБСОРБЦИИ ГАЗОВ // Современные проблемы науки и образования. 2014. № 6. ;URL: https://science-education.ru/ru/article/view?id=15421 (дата обращения: 06.07.2025).



