Бицентрическое монофокусное полупространство (БМП) изучает физико-биологическое иллюзорно-статическое восприятие зрительных образов пространственных объектов глазами человека. На его основе разработана математическая и интерактивная компьютерная модель Glane [5] искажения трёхмерного пространства при параллельном переносе поверхности относительно радиус-вектора фокуса в направлении начала координат, выполненная в рамках государственного контракта № 14.740.11.1149.
Цель исследования
Необходимо произвести ряд экспериментов с помощью компьютерной модели Glane [5], наглядно реализующей положения БМП-подхода [2], и выявить, какие именно факторы влияют на искажение поверхности в процессе произведения над ней преобразования параллельного переноса в БМП [3].
Выбор испытуемых объектов
В качестве исходных данных для эксперимента выступают параметры модели БМП и координаты точек исходной поверхности. Ключевую роль в получении результатов опытов играет не столько форма самой поверхности, сколько входные данных модели БМП.
Следует подобрать поверхность, искажения которой будут наиболее показательны, например, плоскую поверхность, ограниченную плоской симметричной фигурой, такую как упрощённая октаграмма с зеркально поворотной осевой симметрией 8-го порядка [4].
Поиск способа получения результатов эксперимента
Результаты проведения преобразований над поверхностью выводятся в окно отображения графического контекста OpenGL программы Glance [5] и выдаются в качестве таблиц координат точек искажённой поверхности и зрительных областей точек поверхностей (LOR-областей) [3]. Взаимосвязь графических и табличных данных несёт мало информации для оглашения каких-либо выводов.
Преобразование параллельного переноса над точкой в БМП [3] напоминает преобразование гомотетии [1]. Несмотря на ряд существенных различий между ними, их сравнение вполне резонно, поскольку оба они преподносят одну и ту же идею, воплощаемую в различных условиях. Их общим смысловым ядром является описание принципа построения подобных фигур с опорой на заданный в пространстве центр (центры): гомотетия реализует его в евклидовом пространстве [1], а БМП-подход - в рамках субъективной модели представления традиционного трёхмерного пространства человеческим сознанием [3].
Целесообразность сравнения рассматриваемых преобразований подтверждает опыт [3] с двумя обыкновенными карандашами разной длины, толщиной которых пренебрегают. Испытатель держит в одной вытянутой руке длинный карандаш (отрезок P1Q1) и смотрит на его середину (точку F1). Другой рукой берёт короткий карандаш (отрезок P2Q2) и переводит взгляд в его центр. Затем испытатель начинает приближать к себе короткий карандаш, не отрывая глаз от его середины, и пытается зафиксировать момент, когда этот карандаш полностью закроет длинный - тогда точкой фокуса станет F2.
В данной грубой модели параллельного переноса в БМП длинный карандаш (отрезок P1Q1) - это исходный объект, а короткий - смещённый объект (отрезок P2Q2). В ходе испытания короткий и длинный карандаши кажутся наблюдателю идентичными. На самом же деле отрезки P1Q1 и P2Q2 гомотетичны. Если бы короткий карандаш (отрезок P2Q2) изменил форму на дугообразную (дуга UPI2QI2), то всё равно казался бы равным длинному карандашу (отрезок P1Q1) - в БМП эти фигуры считаются идентичными.
Таким образом, итоги эксперимента могут быть представлены результатами сравнения выходных данных после преобразований гомотетии и параллельного переноса в БМП при одинаковых начальных условиях.
Выбор критерия оценки результатов эксперимента
В БМП на положение и форму искажённого объекта влияют координаты точек поверхности смещённого зрительного эллипсоида [3], которые при постоянных зрительных центрах зависят от точки смещённого фокуса [3]. Отличие объекта-результата от исходного обусловлено разной длиной радиус-векторов исходного и смещённого фокуса.
В гомотетии расположение и форма конечной поверхности зависит от координат начальной поверхности относительно центра и коэффициента подобия k [1].
Для построения фигуры, гомотетичной исходной, логично выбрать в качестве коэффициента подобия k частное длин радиус-векторов RIIf и RIf смещённого и исходного фокуса: k = RIIf / RIf, где k ≠ 0, k ϵ (0; 1], RIf ϵ (0; ∞], RIIf ϵ (0; RIf]. Тогда для построения любой точки поверхности, гомотетичной изначальной, будет использоваться следующее выражение: RIIIT = k ∙ RIT, где RIT и RIIIT - длины радиус-векторов от начала координат до взаимосвязанных точек исходной поверхности и соответствующей ей гомотетичной поверхности. Теперь из выражений выше можно получить критерий оценки результатов эксперимента (оценочный критерий) λ: λ = RIIIT / RIIT = k ∙ RIT / RIIT =RIIf / RIf ∙ RIT / RIIT, где λ ϵ (0; +∞); k ϵ (0; 1] - коэффициент подобия; RIf и RIIf - длины радиус-векторов исходного и смещённого фокуса; RIT, RIIT и RIIIT - длины радиус-векторов от начала координат до точек исходной поверхности, смещённой поверхности и соответствующей для исходной поверхности гомотетичной поверхности.
Смысл оценочного критерия λ заключается в численном выражении степени искривления результирующей поверхности относительно гомотетичной.
Разделение испытаний на категории
Результаты будут показательны, если систематизировать тесты по группам, в каждой из которых изменяется только один из параметров экспериментальной модели в то время, как остальные преимущественно зафиксированы.
Тесты категории 1: выявление зависимости оценочного критерия от показателя зрительного центра. Устанавливаются начальные параметры испытательной модели, такие, чтобы смещённая поверхность приобрела явно несимметричную форму. Это случай общего вида в распределении точек поверхностей по областям приоритетов зрительных центров [3]: точка фокуса не принадлежит ни одной из координатных плоскостей.
Для каждой из точек полученной смещённой поверхности рассчитывается критерий оценки результатов эксперимента λ и расстояние до соответствующего зрительного центра.
В условиях проводимого опыта каждая точка поверхности может оказаться под влиянием любого центра, центровые прямые, соединяющие точки поверхностей с соответствующими зрительными центрами [3], исчерчивают пространство под самыми различными углами. Значит, для каждой точки искажённой поверхности стоит учитывать углы наклона центровой прямой к координатным осям. Расчёт всех трёх углов для каждой точки повышает трудоёмкость эксперимента. Проще определять углы наклона проекций центровых отрезков на координатные плоскости к координатным осям. Но одновременный учёт всех таких углов сделает результат эксперимента непоказательным, следовательно, лучше остановиться на одном, наиболее важном угле. Это δ - угол наклона к оси абсцисс проекции на XOY центрового отрезка между точкой зрительного центра и точкой смещённой поверхности. Плоскость XOY выбрана потому, что на ней проекции зрительных центров не сливаются в одну точку, и это позволяет по знаку тригонометрической функции определить положение точки искажённой поверхности относительно соответствующего зрительного центра [2]. Тогда функцией для контроля углов становится косинус: знак показывает квадрант проекции точки результирующей поверхности, а модуль значения - угол отклонения от оси OX (чем меньше модуль косинуса, тем ближе точка поверхности к полуплоскости YOZ [1], находящейся между зрительными центрами).
Расстояние от точки результирующей поверхности до соответствующего зрительного центра можно связать с косинусом δ при помощи величины ρ - показателя зрительного центра, формула которого показана на рис. 1.

Рисунок 1. Расчёт показателя зрительного центра ρ
На рис. 1 показатель зрительного центра ρ - произведение расстояния от точки смещённой поверхности до соответствующего зрительного центра и косинуса угла δ наклона проекции центрового отрезка к оси абсцисс; G - точка зрительного центра: левый L, правый R или средний O, имеющий приоритет над заданной точкой поверхности; xG - проекция точки G на ось OX (xG = ‒dпри G = L, xG = dпри G = Rи xG = 0при G = O, где 2d- межцентровое расстояние); TII (xIIT; yIIT; zIIT) - смещённая точка с трёхмерными координатами, находящаяся под влиянием точки G (должны выполняться условия: xIIT ≠ xG, yIIT ≠ 0); GTII - центровой отрезок между точкой зрительного центра и точкой смещённой поверхности; GTIIxy - проекция отрезка GTII на XOY; GTIIx и GTIIy - проекции отрезка GTII на оси OX и OY соответственно; δ - угол наклона GTIIxy к оси абсцисс.
Суть показателя зрительного центра ρ заключается в том, что, во-первых, его знак даёт информацию о месторасположении точки поверхности относительно плоскости, проходящей через соответствующий зрительный центр параллельно YOZ, а, во-вторых, ρ позволяет судить о величине расстояния от точки поверхности до соответствующего зрительного центра, таким образом, ρ - индикатор положения точки относительно её центра.
По завершении эксперимента имеется следующее заключение.
- Оценочный критерий λ определён на интервале (0; 1]. Чем больше его значение, тем точка смещённой поверхности менее искажена. При λ = 1 искажений нет.
- Если показатель зрительного центра ρ отрицателен, то для наблюдателя точка смещённой поверхности лежит левее соответствующего зрительного центра, при ρ > 0 - правее. Когда ρ = 0, абсцисса такой точки совпадает с абсциссой её зрительного центра.
- Чем больше модуль ρ, тем дальше точка от её зрительного центра.
- Точки, более удалённые от влияющих на них зрительных центров, искажаются больше.
- В целом зависимость λ от ρ можно назвать функциональной, близкой к функции ΨИ = λ(ρ) = 1 / (n ∙ |ρ| + 1) (n - коэффициент сжатия по оси ρ), кроме случая ρ = 0.
- Точки с равными соответствующими значениями λ и ρ всегда симметричны относительно плоскости XOY. При равенстве оценочных критериев λ и противоположных показателях зрительных центров ρ (при этом по модулю они равны) в случае равенства аппликат точки симметричны относительно плоскости YOZ, а при их противоположных значениях - симметричны относительно оси OY.
- Искажённая поверхность получается несимметричной из-за неравномерности распределения LOR-областей [3] и под влиянием межцентрового расстояния.
Тесты категории 2: выявление зависимости оценочного критерия от межцентрового расстояния. Серии этих экспериментов основаны на изменении межцентрового расстояния 2d с сохранением радиус-векторов исходного и смещённого фокуса. По завершении эксперимента имеются следующие итоги.
- Оценочный критерий λ определён на интервале (0; 1]. Чем больше значение λ, тем точка смещённой поверхности менее искажена. При λ = 1 искажений нет.
- Одному значению межцентрового расстояния 2d соответствует единственное значение оценочного критерия λ - их зависимость функциональная.
- Чем меньше межцентровое расстояние 2d, тем больше фокусные полуэллипсоиды походят на полусферы.
- Если две точки исходной поверхности расположены в плоскости, параллельной XOY, и обладают симметрией относительно хотя бы одной из координатных осей или плоскости, проходящей через ось OY, то соответствующие точки смещённой поверхности стремятся к симметрии при уменьшении межцентрового расстояния 2d, так что при 2d = 0 (монокулярное зрение [2]) они вновь становятся симметричными, потому что искажены в равной степени (значения их оценочных критериев λ равны).
- Если при изменении одного лишь параметра межцентрового расстояния 2d при двух ненулевых различных значениях 2d точки смещённой поверхности симметричны, то при таких условиях изменения параметров БМП они остаются симметричными всегда.
- Чем дальше точка от приоритетного зрительного центра, тем меньше её искажение с уменьшением значения 2d.
Тесты категории 3: выявление зависимости оценочного критерия от длины радиус-вектора смещённого фокуса. Данные эксперименты нацелены на изменение длины радиус-вектора смещённого фокуса при постоянном межцентровом расстоянии 2d и неизменных углах между этим вектором и координатными осями. Выводы по экспериментам следующие.
1. Оценочный критерий λ определён на интервале (0; 1]. Чем больше значение λ, тем точка смещённой поверхности менее искажена. При λ = 1 искажений нет.
2. При совпадении фокусных радиус-векторов Rf II = Rf I смещённая поверхность совпадает с исходной.
3. При равенстве длин радиус-векторов смещённых точек фокуса и поверхности (RT II = Rf II) λ = 1 и такая точка не искажается.
4. При нулевом смещённом фокусном радиус-векторе Rf II = 0 эллипсоид смещённого фокуса вырождается в отрезок и наблюдатель, фактически, не различает окружающие предметы [2].
5. Если точки исходной поверхности обладают симметрией, то соответствующие точки смещённой поверхности стремятся к ним и, следовательно, к симметрии при увеличении длины смещённого фокусного радиус-вектора RIIf, так что при RIIf = RIf точки смещённой поверхности вновь совпадают с соответствующими точками исходной поверхности и становятся не искажёнными и симметричными.
6. Одному значению длины радиус-вектора смещённого фокуса Rf II соответствует единственное значение оценочного критерия λ - их зависимость функциональная, монотонно возрастающая, близкая к логарифмическому виду, показанному на рис. 2.
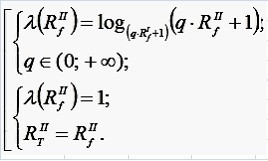
Рисунок 2. Аппроксимация оценочного критерия λ
На рис. 2 λ ϵ (0; 1] - оценочный критерий; RIf ϵ (0; +∞) и RIIf ϵ (0; RIf ] - длины радиус-векторов исходного и смещённого фокуса; RIIT - длина радиус-вектора точки смещённой поверхности; q - основание логарифма для логарифмической зависимости λ от RIIf.
7. Чем меньше длина смещённого фокусного радиус-вектора Rf II, тем меньше фокусные полуэллипсоиды походят полусферы [3].
8. Если длина радиус-вектора RIIT точки смещённой поверхности не равна длине радиус-вектора смещённого фокуса RIIf, то чем меньше величина RIIf, тем точка искажается в большей степени.
9. Точка, принадлежащая участку LOR-области, оказавшемуся с противоположной стороны от своего центра, даже при небольшой степени искривления может значительно усилить асимметрию смещённой поверхности при уменьшении длины радиус-вектора смещённого фокуса RIIf.
10. Если при изменении лишь одной длины радиус-вектора смещённого фокуса RIIf при двух ненулевых различных значениях RIIf точки смещённой поверхности симметричны, то при таких условиях изменения параметров БМП они остаются симметричными всегда.
11. Чем ближе точка поверхности к началу координат, тем меньше её искажение с уменьшением значения RIIf.
Тесты категории 4: выявление зависимости оценочного критерия от распределения областей зрительных приоритетов. Этот вид экспериментов численно сравнивает разные случаи распределения зрительных приоритетов [3] на точки искажённой поверхности в зависимости от углов между радиус-вектором фокуса и координатными осями при постоянном межцентровом расстоянии и радиусах эллипсоида смещённого фокуса. Резюме по итогам итоги проведённого эксперимента категории 4 следующее.
1. Оценочный критерий λ определён на интервале (0; +∞). При λ = 1 точка поверхности не искажается. Степень искажения определяется модулем отклонения λ от 1: Δλ = |1 ‒ λ|.
2. При равенстве длин радиус-векторов смещённых точек фокуса и поверхности (RIIT = RIIf) λ = 1 и такая точка не искажается.
3. Поверхность не искажается, если не перемещается: точки исходного и смещённого фокусов совпадают: RIIf = RIf.
4. Форма поверхности особенно сильно искажается, если её точки попадают в несимметричные зоны виляния зрительных центров.
5. Две точки смещённой поверхности обладают симметрией [4], если соответствующие точки исходной поверхности
- расположены в плоскости, параллельной фронтальной плоскости XOY;
- симметричны относительно хотя бы одной из осей (OX, OY или OZ) или плоскости, проходящей через ось OY;
- находятся под влиянием зрительных центров, симметричных относительно точки O.
В частности симметрия таких точек наблюдается, когда точка фокуса принадлежит OX.
6. Чем дальше точка исходной поверхности от начала координат, тем она больше искажается.
Выводы
По результатам опытов всех четырёх категорий стало ясно, что двумя основными аспектами изучения искажения смещенной поверхности [2] являются изменение кривизны поверхности и поведение симметричных точек.
Форма поверхности зависит от формы эллипсоида смещённого фокуса [3], точнее смещённая поверхность искажается, когда этот эллипсоид начинает отличаться по форме от эллипсоида исходного фокуса. LOR-области играют лишь второстепенную роль в глобальном изменении формы поверхности.
Исчезновение или, наоборот, появление симметрии [4] между точками смещённой поверхности обусловлено распределением областей зрительных приоритетов [3].
Изменение формы эллипсоида смещённого фокуса напрямую зависит от длины радиус-вектора смещённого фокуса, также форма всех зрительных эллипсоидов взаимосвязана с межцентровым расстоянием 2d, косвенно влияющего на изменение формы смещенного эллипсоида при уменьшении смещённого фокусного радиус-вектора [2]. Оценить степень искривления той или иной точки искажённой поверхности позволяет расстояние до её зрительного центра, а с позиции величины λ - расстояние до начала координат.
Для опытов, разделённых на 4 категории, в качестве оценки искажения поверхности был выбран критерий λ. Поскольку в условиях проведённых экспериментов привязка к началу координат была разумна, оценочный критерий λ вычислялся как произведение и отношение длин радиус-векторов и сравнивал искажённую поверхность с фигурой, гомотетичной исходной поверхности, при параллельном переносе вдоль оси OY, так как исходная поверхность была построена параллельно фронтальной плоскости XOZ.
LOR-области [3] распределяются в зависимости от положения точки фокуса, которая характеризуется длиной радиус-вектора и его углами наклона к координатным осям [3]. Именно эти углы формируют зрительно-приоритетные области.
Рецензенты:
Кириллов С.Н., д.т.н., профессор, проректор по научной работе РГРТУ, заведующий кафедрой «Радиоуправление и связь», ФГБОУ ВПО «Рязанский государственный радиотехнический университет», г. Рязань.
Антипов В.А., д.т.н., профессор, профессор кафедры «Информационно-измерительная и биомедицинская техника», ФГБОУ ВПО «Рязанский государственный радиотехнический университет», г. Рязань.
Библиографическая ссылка
Столчнев В.К., Котова Е.А., Пылькин А.Н. АНАЛИЗ РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТОВ ПО ИСКАЖЕНИЮ СМЕЩЁННОЙ ПОВЕРХНОСТИ, ПОЛУЧАЕМЫХ С ПОМОЩЬЮ КОМПЬЮТЕРНОЙ МОДЕЛИ БИЦЕНТРИЧЕСКОГО МОНОФОКУСНОГО ПОЛУПРОСТРАНСТВА // Современные проблемы науки и образования. 2014. № 4. ;URL: https://science-education.ru/ru/article/view?id=14456 (дата обращения: 01.07.2025).



