Математическое моделирование в биомеханике играет важную конструктивистскую роль. Однако, построенные модели ввиду своей сложности трудно доступны медицинским специалистам. В данной работе предлагается рассмотреть информационно-аналитическую систему моделирования компрессионного перелома позвоночника человека (ИАС). Структура предполагаемой ИАС включает в себя следующие компоненты: МРТ, исходные механические параметры системы позвонков, математическую модель системы трех позвонков, параметры возможного фиксатора для стабилизации позвоночника, выходные данные модели, базу данных принятия решения.
Под нестабильностью позвоночника подразумевают такое нарушение взаимодействия между телами позвонков, когда вследствие сугубо механических причин изменяются нормальные законы статики и кинетики позвоночного столба на определенном участке, что проявляется в избыточной и аномальной подвижности тел, некорректных их перемещениях, выходящих за физиологические пределы [7]. Это может являться причиной многочисленных сугубо медицинских проблем, часто требующих хирургических методов лечения [8].
Для правильного хирургического лечения нестабильности позвоночника необходимым условием является оптимальный подбор корригирующих фиксирующих приспособлений, способных предотвратить некорректные перемещения тел позвонков и одновременно максимально точно протезировать нормальные упруго-динамические характеристики связочно-капсульного аппарата позвоночника [2]. Для поиска оптимальных характеристик фиксаторов позвоночника разработана модель трёхпозвонкового комплекса при фиксации крайних позвонков системы жесткой пластиной [4]. Результатами исследований является предпочтение использования гибкого фиксатора, состоящего из пружинных элементов.
Цель исследования
Цель работы – сформулировать структуру и алгоритм работы информационно-аналитической системы моделирования компрессионного перелома позвоночника человека, позволяющую испытать виртуально фиксатор, применяемый в хирургической операции на позвоночнике.
Материалы и методы исследования
Материал исследования – математическая модель компрессионного перелома позвоночника человека, рассматриваемая на трехэлементном участке позвоночника. Участок представлен телами позвонков с дугоотростчатыми суставами, которые связаны между собой упруго-демпфирующими элементами (межпозвоночные диски, мышечно-связочный аппарат) и двумя фиксирующими пластинами (рис. 1).
Результаты исследования и их обсуждение
Расчетная схема фрагмента позвоночника человека, состоящая из трех позвонков с клиновидным средним позвонком и стабилизирующими конструкциями представлена на рис.1 с вариантом клиновидной деформации среднего позвонка и двумя стабилизирующими конструкциями (для передних и заднего опорных комплексов). Предел прочности, упругая деформация и коэффициенты жесткости различных участков позвоночника задаются для каждого отдела позвоночника согласно таблицам А.П. Громова [1]. Для фиксации позвоночника предусмотрено применение плоскостных конструкций с коэффициентами жесткости Сст1 и Сст2, что позволяет моделировать, как жесткие системы, так и пружинные элементы, изготовленные из различных материалов.
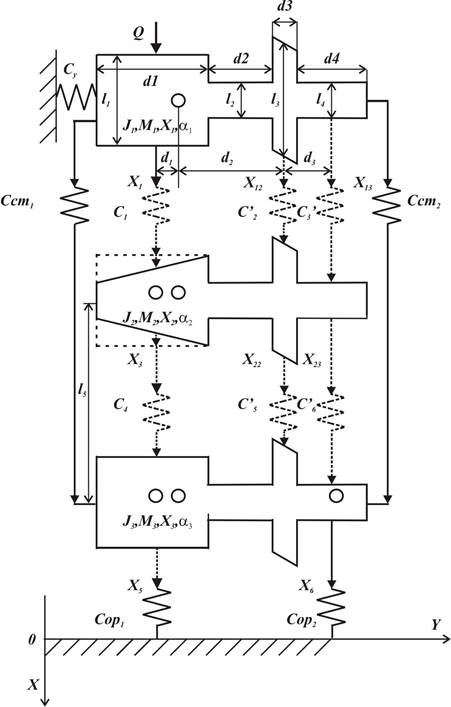
Рис. 1. Расчётная схема трёхпозвонкового комплекса человека
Ji, Мi, Xi- момент инерции, масса, координата i-го позвонка (i = 1,2,3); Cсmj -коэффициенты жесткости j-й стабилизирующей пластины (j = 1,2); Сopj - коэффициенты жесткости j-й опоры (j = 1,2); d1, d2, d3, d4, di, li, - линейные размеры позвонков; Qk - внешние воздействия
Математическая модель компрессионного перелома человека построена на основе уравнения Лагранжа II рода, имеет вид:
![]() , (1)
, (1)
где А = М-1 С; ![]() ; F =
; F = ![]() . Матрицы системы имеют вид:
. Матрицы системы имеют вид:
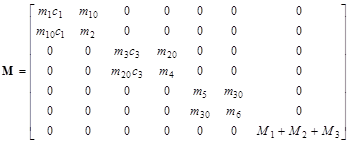 ;
;
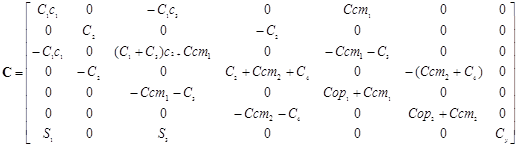
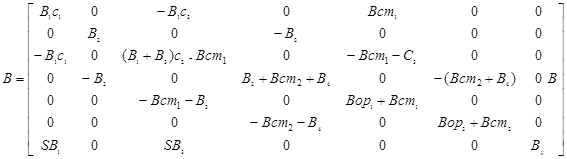
![]() Х=
Х=![]()
В качестве обобщенных координат xk принимались следующие координаты:
х1; х2; х3; х4 (α1 = ![]() ); х5; х6 (
); х5; х6 (![]() );у, где Di = d1 + d2, i = 1,2,3.
);у, где Di = d1 + d2, i = 1,2,3.
Для сокращения матричных элементов также введены обозначения:
с1= cos(β1), c3= cos(β3), S1= С1 x1·sin(β1)·cos(β1), S3=С3·x3·sin(β3)·cos(β3), SB1= B1 x1·sin(β1)·cos(β1), SB3= B3 x3·sin(β3)·cos(β3).
Система обыкновенных дифференциальных уравнений второго порядка с постоянными коэффициентами (1) сводится к системе 14-ти обыкновенных дифференциальных уравнений первого порядка в векторной форме, имеет следующий вид:
![]()
![]() (2)
(2)
Алгоритм численного решения системы векторных уравнений (2) записывается в виде:
![]()
![]() (3)
(3)
Для каждого варианта приложения внешней силы Q рассчитаны нормальные нагрузки на третий позвонок трёхпозвонкового комплекса человека при отсутствии патологии и фиксирующих устройств. На рисунке представлены нагрузки на центральный и задний столб третьего позвонка при приложенной силе в центре тяжести. Для оптимизации в качестве нормальных (физиологических) выбраны следующие нагрузки (рис. 2):
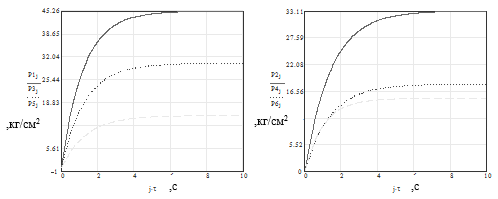
Рис. 2. Нагрузки Р1, Р3, Р5, действующие на центральный (слева) и на задний (справа) столбы в зависимости от времени
Результаты наших расчётов дают оптимальный интервал жесткости стабилизирующей пластины 609.4<Cct1<6403.6 H/мм. Это позволяет сделать вывод, что вычисленный интервал жесткости, позволит продолжить изыскания надежного фиксатора нового поколения для лечения нестабильных состояний позвоночника, обусловленных клиновидной деформаций среднего позвонка или разрушением его передних колонн [3].
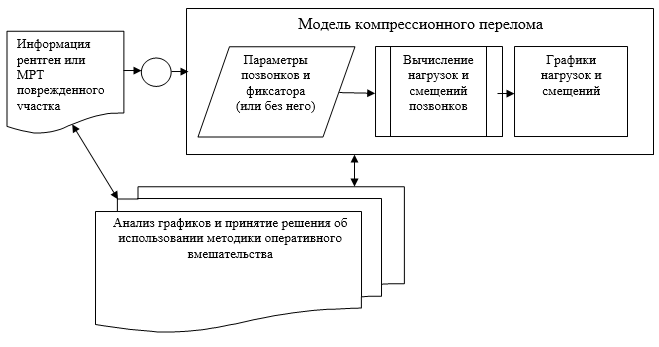
Рис. 3. Схема информационно-аналитической системы моделирования компрессионного перелома позвоночника человека
По данным математического моделирования, в условиях нестабильного положения позвоночника, связанного с разрушением межпозвонкового диска или тела позвонка, в том числе, с изменением его упруго-прочностных свойств или геометрических параметров, оптимальным вариантом его стабилизации является применение фиксирующих конструкций упругого типа (например, транспедикулярных систем с пружинными штангами из NI-NI сплава или системы «Dynesis»). Это позволяет сохранить распределение эпюр нагрузок на тела позвонков в пределах значений близких к природным - 0,7 / 0,3 [5]. Представленная на рис. 3 информационно-аналитическая система, позволит моделировать смещение тел позвонков в допустимых пределах, предотвращая сдавливание спинного мозга. Предварительные испытания фиксатора на математической модели приведут к точному обоснованию применения вида фиксатора позвоночника в конкретном случае.
Выводы и заключение
- Формирование информационно-аналитической системы моделирования компрессионного перелома создает возможность глубже использовать точные методы предварительных апробаций фиксаторов позвоночного столба.
- При нестабильности позвоночника более физиологично применение динамических фиксирующих систем.
- Применение динамических фиксирующих систем при межтеловой стабилизации является профилактикой раннего износа смежных дисков в системе.
Рецензенты:
Мартынов А.Ф., д.э.н., профессор, профессор кафедры информатики и математики Санкт-Петербургского Гуманитарного университета профсоюзов, г.Санкт-Петербург.
Марьяненко В.П., д.э.н., профессор, профессор кафедры общей экономической теории Санкт-Петербургского государственного экономического университета, г.Санкт-Петербург.
Пучиньян Д.М., д.м.н., профессор, зам. директора по науке, ФГБУ «Саратовский научно-исследовательский институт травматологии и ортопедии» Министерства здравоохранения и социального развития Российской Федерации, г. Саратов.
Библиографическая ссылка
Седов Р.Л., Орлов С.В., Бобарыкин Н.Д. ИНФОРМАЦИОННО-АНАЛИТИЧЕСКАЯ СИСТЕМА МОДЕЛИРОВАНИЯ КОМПРЕССИОННОГО ПЕРЕЛОМА ПОЗВОНОЧНИКА ЧЕЛОВЕКА // Современные проблемы науки и образования. 2014. № 4. ;URL: https://science-education.ru/ru/article/view?id=14252 (дата обращения: 17.11.2025).



