Комбинированная система управления состоит из нескольких контуров управления и используется при сильных и динамично изменяющихся возмущающих воздействиях, оказывающих большое влияние на регулируемые параметры. Такая структура системы регулирования применяется когда наличие только замкнутого контура системы управления (управление по отклонению) не может обеспечить устойчивость системы или требуемое качество регулирования. Количество сильных возмущающих воздействий обычно невелико, а каналы возмущения поддаются математическому описанию. В разомкнутом контуре (управление по возмущению) используют динамический компенсатор, позволяющей системе управления действовать на упреждение при изменении возмущающего воздействия, не дожидаясь реакции объекта на это изменение. Выходное воздействие разомкнутого контура обычно складывается с воздействием замкнутого контура. На рис. 1 представлена структура простейшей комбинированной системы управления с одним регулируемым параметром y, одним возмущающим z и одним регулирующим воздействием x. Wx - передаточная функция канала регулирования, Wz - передаточная функция канала возмущения. Толстой линией показан объект управления.
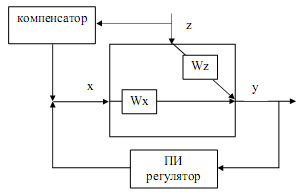
Рисунок 1. Структура комбинированной системы управления
Если каналы возмущения и регулирования трудно описать на основе физических, химических и т.п. уравнений, то для их описания обычно используются стандартные звенья. Подавляющее большинство объектов управления являются объектами с самовыравниванием, зависимости входных и выходных параметров для них часто описывают с помощью апериодического звена первого порядка с запаздыванием. Передаточная функция такого звена (1) характеризуется тремя параметрами: коэффициент усиления k, постоянная времени T и чистое запаздывание τ.
Точное знание этих параметров для канала возмущения и регулирования позволяет теоретически рассчитать оптимальные настройки ПИ регулятора, определить тип и настройки компенсатора, обеспечив высокое качество работы системы управления. Система передаточных функций Wx и Wz с найденными значениями k, T и τ для каждой из них является математической моделью объекта. Кроме того, что идентификацию параметров объекта управления необходимо произвести при наладке системы управления для ее первичной настройки, также весьма желательно периодически уточнять найденные значения во время эксплуатации.
Существует два способа идентификации параметров объекта управления: на основе эксперимента и на основе наблюдения. Первый заключается в снятии кривой разгона в отдельности для каждого канала, второй не требует вывода из работы системы регулирования и представляет гораздо больший интерес.
Классическим методом идентификации является метод наименьших квадратов МНК. Целевой функцией является сумма квадратов ошибок (невязок) по всему рассматриваемому диапазону. Оптимизирующие факторы - параметры модели. В качестве решения выбираются такие значения оптимизирующих факторов, которые обеспечивают минимум целевой функции. При переходе от одного значения оптимизирующего фактора к следующему могут использоваться следующие поисковые методы: метод сканирования, метод градиента, симплексный метод, метод случайных чисел и др.
Ограничения, накладываемые МНК при идентификации объекта управления: отсутствие стационарности параметров (чтобы детерминированная составляющая сигнала превышала случайную составляющую), достаточная длина диапазона, сравнимая с инерционностью исследуемого канала, небольшое число оптимизирующих факторов.
Для рассматриваемого объекта для идентификации вполне можно использовать МНК в его классической форме, однако когда число регулируемых параметров, регулирующих и возмущающих воздействий гораздо больше, этот метод не обеспечивает высокой точности. В качестве решения предлагается вносить во входное воздействие (в т.ч. возмущающее) дополнительную периодическую составляющую и затем выделять из выходного сигнала реакцию объекта на нее (см. рис. 2). Таким образом, можно разбить задачу идентификации на более мелкие. Можно рассматривать каналы по отдельности, число оптимизирующих факторов в каждой задаче снижается до трех. Внесением во входной сигнал дополнительной составляющей мы избавляемся от возможной стационарности как входного, так и выходного сигнала.
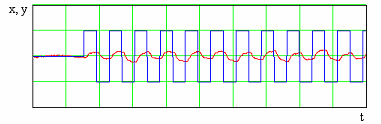
Рисунок 2. Дополнительная периодическая составляющая входного сигнала и реакция на нее объекта управления
Если идентифицируются параметры объекта по каналам возмущения, то для того, чтобы реакция на периодическую составляющую не была искажена влиянием замкнутого контура регулирования, на время идентификации выключаем его из работы.
Библиографическая ссылка
Забиров Р.Р. ИДЕНТИФИКАЦИЯ ПАРАМЕТРОВ ОБЪЕКТА УПРАВЛЕНИЯ ПРИ КОМБИНИРОВАННОЙ СИСТЕМЕ РЕГУЛИРОВАНИЯ // Современные проблемы науки и образования. 2005. № 1. ;URL: https://science-education.ru/ru/article/view?id=128 (дата обращения: 08.02.2026).



