Введение
В работах [5-9] отмечено, что распознавание технических состояний сложных строительных систем вполне укладывается в понятия и возможности математических методов теории технической диагностики. А в монографии [2] совершенно справедливо указано, что конечной целью диагностики состояний является повышение надежности и ресурса систем и что техническую диагностику вообще следует рассматривать как один из основных разделов общей теории надежности.
Для оценки технического состояния, т.е. для определения категорий технического состояния элементов зданий в соответствии с [3; 4], предложен подход, основанный на теоретическом аппарате технической диагностики, использующем вероятностные методы распознавания состояний сложных технических систем. Диагностирование выполняется статистическим методом с применением обобщенной формулы Байеса [2; 5–9]
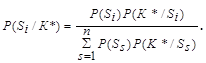 (1)
(1)
После вычисления апостериорных вероятностей состояний P(Si/K*) [2; 7] для каждого конструктивного элемента по указанной зависимости осуществляется анализ полученных результатов с использованием аппарата теории информации, в частности, с использованием понятий информационной энтропии [2; 7; 8; 10]. Этот подход использован при построении многоуровневой иерархической модели диагностирования [8; 9]. В настоящей работе именно на этой основе предлагается выполнить и оценку надежности. Такую модель диагностирования для строительных конструкций зданий предлагается применить впервые, что определяет научную новизну работы.
Отмечено [1], что для оценки надежности других технических систем нашел применение и достаточно хорошо развит вероятностно-статистический подход. Однако эти системы характеризуются массовостью изготовления, в связи с чем имеется возможность получить достаточно представительную статистику отказов не только отдельных элементов, но и систем в целом. Для строительных систем такой подход неприемлем, т.к. для них нет полноценной статистики отказов ни для элементов, ни для объекта в целом. Вместе с тем для этих зданий накопился значительный материал по статистике диагнозов (состояний) и по статистике определяющих эти диагнозы признаков, который удалось упорядочить и уложить в рамки уже имеющихся разработанных методик теоретического аппарата технической диагностики и теории информации. Полученные на этой основе результаты диагностирования состояний строительных систем и их элементов позволяют несколько по-иному посмотреть и на проблему надежности, и на ее решение.
Предложенный подход рассматривается далее на примере диагностирования и оценки надежности главных балок железобетонного монолитного междуэтажного перекрытия здания старой городской застройки, выполненного по схеме балочной клетки. Перекрытие представляется как сложная конструктивная подсистема некоторого промежуточного уровня, являющаяся конструктивным элементом системы следующего, более высокого уровня – здания в целом. Перекрытие состоит из главных балок Gk (k = 1, 2, 3, …, g), второстепенных балок Wk (k = 1, 2, 3, …, w), плитных участков Fk (k = 1, 2, 3, …, f) и колонн Lk (k = 1, 2, 3, …, l), которые рассматриваются как его элементы и группы элементов. Схема раскладки этих элементов показана на рис. 1. Как видно, в данном примере перекрытие состоит из трех главных балок G1, G2 и G3 (g = 3), двадцати двух второстепенных балок Wk (w = 22), двадцати четырех плитных участков Fk (f = 24) и двух колонн Lk (l = 2).
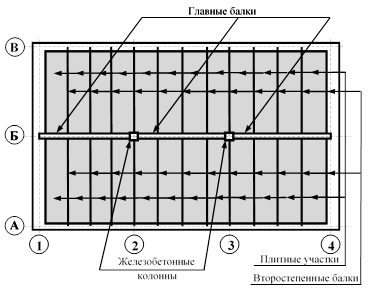
Рис. 1. Схема раскладки элементов перекрытия
Использование статистических методов технической диагностики, в частности метода Байеса, предусматривает сбор, обработку и упорядочивание статистической информации по данным обследований прошлых лет. Весь статистический материал удобно представить в виде так называемых диагностических матриц. Для главных балок рассматриваемого перекрытия диагностическая матрица имеет вид таблицы 1. Как видно, приняты пять состояний диагностирования с названиями в соответствии с [4] и с априорными вероятностями P(Si), а также девять признаков (простых и трехразрядных [5]) с вероятностями pg(kjs/Si) [6; 8]. Данные для диагностической таблицы получены при обработке результатов ретроспективного анализа состояний ста главных балок. Далее предполагается, что при последующих обследованиях аналогичных балок были получены следующие реализации указанных в таблице 1 признаков.
Таблица 1
Диагностическая матрица для главных балок перекрытия
|
№ № п/п |
Диагностические п р и з н а к и |
kjs |
Разр призн. |
p(kjs) |
Сост. S1 |
Сост. S2 |
Сост. S3 |
Сост. S4 |
Сост. S5 |
|
P(S1) |
P(S2) |
P(S3) |
P(S4) |
P(S5) |
|||||
|
0,18 |
0,29 |
0,35 |
0,13 |
0,05 |
|||||
|
1 |
Поврежд. бетона, сниж. его св-ва по отн. к арм. |
k11 |
да |
p(k11) |
0,11 |
0,17 |
0,29 |
0,54 |
0,80 |
|
k12 |
нет |
p(k12) |
0,89 |
0,83 |
0,71 |
0,46 |
0,20 |
||
|
2 |
Прод. трещины в защ. слое вдоль армат. стержней |
k21 |
да |
p(k21) |
0,06 |
0,14 |
0,23 |
0,77 |
0,60 |
|
k22 |
нет |
p(k22) |
0,94 |
0,86 |
0,77 |
0,23 |
0,40 |
||
|
3 |
Нормальные трещины (ширина раскрытия) |
k31 |
< 0,4 мм |
p(k31) |
0,76 |
0,59 |
0,40 |
0,15 |
0,20 |
|
k32 |
до 1,0 мм |
p(k32) |
0,18 |
0,34 |
0,43 |
0,62 |
0,40 |
||
|
k33 |
≥ 1,0 мм |
p(k33) |
0,06 |
0,07 |
0,17 |
0,23 |
0,40 |
||
|
4 |
Наклонные трещ. (наличие) |
k41 |
да |
p(k41) |
0,06 |
0,17 |
0,34 |
0,31 |
0,20 |
|
k42 |
нет |
p(k42) |
0,94 |
0,83 |
0,66 |
0,69 |
0,80 |
||
|
5 |
Прочность бетона |
k51 |
проектная |
p(k51) |
0,72 |
0,48 |
0,49 |
0,15 |
0,20 |
|
k52 |
≤ 30% |
p(k52) |
0,22 |
0,31 |
0,20 |
0,39 |
0,20 |
||
|
k53 |
> 30% |
p(k53) |
0,06 |
0,21 |
0,31 |
0,46 |
0,60 |
||
|
6 |
Коррозия арматуры |
k61 |
< 5% |
p(k61) |
0,76 |
0,59 |
0,29 |
0,15 |
0,20 |
|
k62 |
5 – 20 |
p(k62) |
0,18 |
0,24 |
0,37 |
0,39 |
0,20 |
||
|
k63 |
> 20% |
p(k63) |
0,06 |
0,17 |
0,34 |
0,46 |
0,60 |
||
|
7
|
П р о г и б |
k71 |
допускаем. |
p(k71) |
0,83 |
0,48 |
0,51 |
0,31 |
0,20 |
|
k72 |
≤ 30% |
p(k72) |
0,11 |
0,38 |
0,23 |
0,46 |
0,20 |
||
|
k73 |
> 30% |
p(k73) |
0,06 |
0,14 |
0,26 |
0,23 |
0,60 |
||
|
8 |
Условие прочности по нормальным сечениям |
k81 |
да |
p(k81) |
0,94 |
0,90 |
0,86 |
0,69 |
0,20 |
|
k82 |
нет |
p(k82) |
0,06 |
0,10 |
0,14 |
0,31 |
0,80 |
||
|
9 |
Условие прочности по наклонным сечениям |
k91 |
да |
p(k91) |
0,94 |
0,83 |
0,60 |
0,61 |
0,20 |
|
k92 |
нет |
p(k92) |
0,06 |
0,17 |
0,40 |
0,39 |
0,80 |
Для сто первой балки: первый признак – «k11»; второй признак – «k21»; третий признак – «k31»; четвертый признак – «k41»; пятый признак – «k52»; шестой признак – «k61»; седьмой признак – «k71»; восьмой признак – «k81»; девятый признак – «k92». В качестве примера для этой балки реализации признаков в таблице 1 выделены цветом.
Для сто второй балки: первый признак – «k11»; второй признак – «k21»; третий признак – «k31»; четвертый признак – «k41»; пятый признак – «k53»; шестой признак – «k63»; седьмой признак – «k71»; восьмой признак – «k81»; девятый признак – «k91».
Для сто третьей балки: первый признак – «k11»; второй признак – «k21»; третий признак – «k32»; четвертый признак – «k42»; пятый признак – «k53»; шестой признак – «k63»; седьмой признак – «k71»; восьмой признак – «k82»; девятый признак – «k91». Очевидно, что для сто второй и сто третьей балок выделение строчек цветом в диагностической матрице будет иным.
После проведения серии расчетов по зависимости (1) распределение апостериорных вероятностей состояний P(Si/K*) для каждой балки получилось в виде следующих численных значений (таблица 2, столбцы 2, 3, 4, 5, 6).
Таблица 2
Численные значения вероятностных параметров состояний и надежности для главных балок
|
Элементы |
P(S1/K*) |
P(S2/K*) |
P(S3/K*) |
P(S4/K*) |
P(S5/K*) |
P(Sf) |
P(Snf) |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
Балка G1 |
0,008 |
0,167 |
0,582 |
0,221 |
0,022 |
0,022 |
0,978 |
|
Балка G2 |
0,055 |
0,378 |
0,404 |
0,160 |
0,003 |
0,003 |
0,997 |
|
Балка G3 |
0,000 |
0,007 |
0,080 |
0,677 |
0,236 |
0,236 |
0,764 |
|
Все главн. балки |
0,014 |
0,131 |
0,300 |
0,432 |
0,123 |
0,123 |
0,877 |
Очевидно, что построчная сумма вероятностей в столбцах 2–6 этой таблицы равна единице во всех ее строках.
В последней (нижней) строке таблицы представлено распределение апостериорных вероятностей состояний для объединенной группы элементов «главные балки». Результат получен на основе уровневого построения решения с применением основных понятий методов теории информации. Использованы ее основные понятия: информационная энтропия (степень неопределенности состояний системы), максимальная энтропия, остаточная энтропия (степень определенности состояний системы или количество внесенной информации) и вероятности степени определенности. Применен также предложенный автором «передаточный механизм» вероятностной оценки состояний посредством расчетов информационного вклада (доли) состояний каждой балки в состояние структуры следующего уровня – в данном случае объединенной группы элементов «главные балки». В работах [6; 8; 9] построение решения на основе модели иерархической уровневой структуры диагностирования в виде «диагностического дерева» рассмотрено более подробно. В настоящее время такой подход реализован и для здания в целом.
Методику расчета надежности с использованием полученных результатов вероятностного анализа технического состояния рассматриваемых конструктивных элементов перекрытия предлагается рассмотреть именно на примере представленных в таблице 2 вероятностных параметров. В основу построения методики положен принцип разделения и последующего комбинирования полученных по расчетам вероятностей пяти состояний. Последовательность решения этой задачи в данном случае состоит в следующем.
1. Выполняется разделение, а затем комбинирование пяти априорных вероятностей состояний по принципу 4 + 1 (таблица 1), т.е., например, для балки G1
P(Snf) = P(S1) + P(S2) + P(S3) + P(S4), а P(Sf)= P(S5). (2)
2. По такому же принципу разделяются и объединяются получаемые в результате расчетов по формуле (1) пять апостериорных вероятностей, т.е. для балки G1 можно записать
P(Snf/K*) = P(S1/K*) + P(S2/K*) + P(S3/K*) + P(S5/K*), а P(Sf/K*) = P(S5/K*). (3)
3. Принимается решение о том, что апостериорная вероятность пятого аварийного состояния P(S5/K*), характеризующегося по определению исчерпанием несущей способности элемента [4], группы элементов и системы в целом, рассматривается как вероятность отказа P(Sf/K*). Вероятность состояния, которая обозначена P(Snf/K*) и которая объединяет первые четыре вероятности состояний, в таком случае представляется как вероятность безотказной работы, т.е. надежность. Очевидно, что вероятность безотказной работы
P(Snf/K*) = 1 – P(Sf/K*). (4)
В данном примере численные значения P(Sf/K*) и P(Snf/K*) в таблице 2 для всех трех балок приведены в столбцах 7 и 8 соответственно.
Анализируя данные в столбце 8, можно отметить, что группа из трех элементов (трех балок) имеет некоторое резервирование надежности, т.е. не относится однозначно к системам с последовательным соединением элементов. При последовательном соединении элементов, как известно, надежность системы определяется произведением надежностей составляющих элементов
P(Gnf) = P(G1nf) · P(G2nf) · P(G3nf) = 0,978 · 0,997 · 0,764 = 0,745 < 0,877. (5)
Не относится эта группа и к системам с параллельным соединением элементов, надежность которых, как известно, определяется зависимостью, представляющей собой сумму вероятностей составляющих элементов, состояния которых рассматриваются как события совместные и независимые
P(Gnf) = P(G1nf) +P(G2nf) +P(G3nf) − P(G1nf) · P(G2nf) −P(G2nf) · (G3nf) −P(G3nf) · P(G1nf) + P(G1nf) · P(G2nf) · P(G3nf) = 0,999 > 0,877. (6)
В формулах (5) и (6) величина P(Gknf) − сумма вероятностей безотказной работы k-й балки (k = 1, 2, 3, …, g), вычисленная по зависимости (3).
Таким образом, надежность группы элементов «главные балки», отражающая их техническое состояние, выявленное при обследовании, попадает в интервал с крайними граничными значениями вероятностей (0,745 – 0,999), причем практически в середину этого интервала. Результат представляется достаточно убедительным. Он убедителен еще и потому, что по результатам выполненных вероятностных расчетов для всех элементов низшего (базисного) уровня иерархии (второстепенные балки, плитные участки и колонны) рассматриваемого перекрытия также были получены близкие соотношения. На рис. 2 показана часть (ветвь) «диагностического дерева» только для группы элементов «главные балки». В ячейках диаграммы, как видно, представлены численные значения максимальных вероятностей состояний и вероятностей безотказной работы, т.е. надежности.

Рис. 2. Часть «диагностического дерева» для главных балок перекрытия
Выводы. Методика расчета показателей надежности по данным выполненного вероятностного анализа технического состояния конструктивных элементов здания предложена на примере результатов диагностирования главных балок монолитного железобетонного междуэтажного перекрытия здания старой городской застройки. В этом случае построенное «дерево диагнозов» стало вполне обоснованной графической моделью оценки надежности, т.е. может рассматриваться как «дерево отказов». В основу построения методики расчета надежности положен принцип разделения и последующего комбинирования полученных по расчетам вероятностей состояний.
Последовательность решения этой задачи состоит в том, что разделение выполнено по схеме «4 + 1». Именно на основе этой формулы принято решение считать вероятность отказа равной апостериорной вероятности пятого аварийного состояния, а вероятность безотказной работы (надежность) определять по зависимости (4).
Рецензенты:
Морозов В.И., д.т.н., профессор, зав. кафедрой железобетонных и каменных конструкций ФГБОУ ВПО «СПбГАСУ», г. Санкт-Петербург.
Белов В.В., д.т.н. профессор кафедры «Строительная механика и строительные конструкции» ФГБОУ ВПО «СПбГПУ», г. Санкт-Петербург.
Библиографическая ссылка
Соколов В.А. ОЦЕНКА ТЕХНИЧЕСКОГО СОСТОЯНИЯ И НАДЕЖНОСТИ СТРОИТЕЛЬНЫХ КОНСТРУКЦИЙ НА ОСНОВЕ ВЕРОЯТНОСТНЫХ МЕТОДОВ ТЕХНИЧЕСКОЙ ДИАГНОСТИКИ // Современные проблемы науки и образования. 2013. № 6. ;URL: https://science-education.ru/ru/article/view?id=11552 (дата обращения: 18.11.2025).



