Введение
В работах [1,2] Л. С. Маянцем и Г. Б. Шалтупером был разработан метод расчета молекулярных колебаний, на основе предложенных ими координат Xδ0. Эти координаты представляют собой компоненты изменений векторов связей в “своих” (для каждой связи) декартовых системах координат, если связь понимать в геометрическом смысле, т.е. в смысле отрезка прямой, соединяющей два атома. Число независимых векторов связей в N-атомной молекуле равно N-1. Таким образом, число независимых координат Xδ0 равно 3N-3. Совокупность этих 3N-3 координат определяет не только деформацию молекулы, но и изменение ее ориентации как целого в пространстве. Поэтому расчет колебаний в этих координатах дает кроме частот и форм собственных нормальных колебаний еще 3 (2 для линейных молекул) частоты и формы малых поворотов молекулы как целого.
Оси Z “своих” (для каждой связи) декартовых систем координат направляются вдоль векторов соответствующих связей. Вместе с тем алгоритм однозначной ориентации осей X и Y “своих” систем координат в работе [1] предложен не был.
Координаты Xδ0 обладают целым рядом достоинств [1,2]. Они также как и валентно-силовые координаты (изменения длин связей, изменения валентных углов и т.д.) легко интерпретируются. Но, в отличие от координат Xδ0 , выбор валентно-силовых координат не может быть универсальным, т.к. во многих случаях не ясно как вводить неплоские координаты [1]. Кроме того, существуют так называемые “неклассические” молекулы, т.е. такие, в которых некоторые естественные координаты вообще теряют смысл. Кроме того, Л. С. Маянцем и Г. Б. Шалтупером была выдвинута гипотеза о возможной переносимости некоторых элементов матрицы Fδ0 в рядах родственных химических соединений. В частности в работе [1] была обоснована, а в работе [3] продемонстрирована переносимость элементов, соответствующих вторым производным функции потенциальной энергии по координатам z (в координатах Xδ0), т.к. этим элементам соответствуют естественные координаты, описывающие растяжение/сжатие связей. К сожалению, несмотря на то, что координаты Xδ0 были предложены 30 лет назад, в настоящее время существует крайне мало публикаций, относящихся к их применению.
Алгоритм ориентации Xδ0 координат
Для анализа свойств матриц Fδ0 нами был разработан алгоритм однозначной ориентации Xδ0 координат. Рассмотрим его подробнее. Прежде всего, следует выбрать сами векторы связей. Так, если в химическом соединении имеются циклы, то общее число связей может превысить N-1, в этом случае достаточное число векторов связей формируется путем нахождения остовного дерева графа, соответствующего молекуле. Далее каждый вектор связи переносится последовательно в начало общей для всей молекулы системы декартовых координат. Введем обозначения: Xi,Yi, Zi – оси, соответствующие “своей” для i-ой связи декартовой системе координат; X, Y, Z – оси, соответствующие общей для всей молекулы декартовой системе координат. Ось Ziориентируется вдоль i-го вектора связи. Оси Xi и Yi находятся путем вращения осей X и Y вокруг вектора k (проходящего через начало общей системы координат и перпендикулярного плоскости, содержащей Z и Zi ) на угол ζ (равный углу между осями Z и Zi ) в направлении от Z к Zi. В качестве вектора k может выступить векторное произведение Zi x Z. Таким образом, в данном алгоритме реализуется своего рода наклон общей системы координат до совмещения оси Z с i-м вектором связи без какого-либо вращения осей Xi, Yi относительно вектора связи. Данный алгоритм ориентации Xδ0 координат является однозначным, не имеет принципиальных математических трудностей при реализации, а также позволяет все векторы связей рассматривать с одинаковых позиций. Последнее свойство алгоритма позволяет выдвинуть гипотезу о равенстве элементов силовой матрицы Fδ0 , соответствующих векторам одинаковых (в смысле химической природы и окружения) связей.
Для проверки этой гипотезы нами был осуществлен расчет матрицы силовых коэффициентов в декартовой системе координат Fx молекулы C3H8 с помощью пакета Gaussian 03W 6.0 [4]. Расчет проводился методом DFT B3LYP в базисе 6-311G (d,p) в гармоническом приближении. После вычисления матрицы Fx пакетом Gaussian она с помощью линейных преобразований переводилась в матрицу Fδ0. Алгоритм соответствующего преобразования следующий:
1. Находим матрицу кинематических коэффициентов ![]() , где Gx – матрица кинематических коэффициентов в декартовой системе координат; Aδ0 – матрица осуществляющая преобразование из декартовой системы координат в систему координат Xδ0, алгоритм составления соответствующей матрицы подробно описан в [1,2].
, где Gx – матрица кинематических коэффициентов в декартовой системе координат; Aδ0 – матрица осуществляющая преобразование из декартовой системы координат в систему координат Xδ0, алгоритм составления соответствующей матрицы подробно описан в [1,2].
2. Находим матрицу ![]()
3. Осуществляем линейное преобразование: ![]()
Следует отметить, что размерность элементов матрицы Fx , полученной при расчетах в Gaussian, составляет хартри/бор2. Но, так как общепринятой размерностью элементов силовых матриц является мдин/Å, нами дополнительно осуществлялось преобразование размерностей из хартри/бор2 в мдин/Å.
Для контроля всех преобразований решали уравнение![]() , сравнивая найденные частоты колебаний с частотами, полученными при расчетах в Gaussian 03W 6.0. Все расчеты, связанные с матричными вычислениями, проводили с помощью пакета программ MATLAB 7.0.1 [5], с его же помощью осуществлялся алгоритм ориентации Xδ0 координат.
, сравнивая найденные частоты колебаний с частотами, полученными при расчетах в Gaussian 03W 6.0. Все расчеты, связанные с матричными вычислениями, проводили с помощью пакета программ MATLAB 7.0.1 [5], с его же помощью осуществлялся алгоритм ориентации Xδ0 координат.
Соответствие частот, полученных при решении векового уравнения, с вычисленными программой Gaussian свидетельствует о правильной работе алгоритма.
Экспериментальные и расчетные частоты колебаний молекулы C3H8 даны в табл. 1. Матрица Fδ0 представлена в
табл. 2.
Таблица 1. Экспериментальные и расчетные частоты колебаний молекулы пропана, см-1.
| Эксперимент | Расчет | Эксперимент | Расчет | Эксперимент | Расчет |
| 2977(a1) | 3086 | 2967(a2) | 3073 | 1338(b1) | 1368 |
| 2962(a1) | 3020 | 1451(a2) | 1492 | 1054(b1) | 1058 |
| 2887(a1) | 3014 | 1278(a2) | 1318 | 922(b1) | 933 |
| 1476(a1) | 1515 | 940(a2) | 913 | 2973(b2) | 3084 |
| 1462(a1) | 1494 | 216(a2) | 221 | 2968(b2) | 3034 |
| 1392(a1) | 1423 | 2968(b1) | 3083 | 1472(b2) | 1510 |
| 1158(a1) | 1176 | 2887(b1) | 3016 | 1192(b2) | 1213 |
| 869(a1) | 871 | 1464(b1) | 1500 | 748(b2) | 753 |
| 369(a1) | 367 | 1378(b1) | 1406 | 268(b2) | 270 |
Наблюдается удовлетворительное согласие теории и эксперимента.
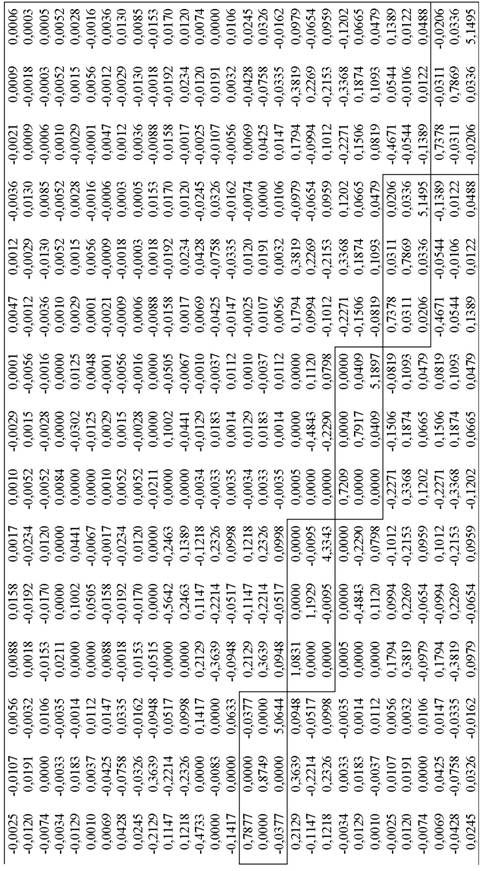
Таблица 2. Матрица Fδ0 молекулы C3H8 рассчитанная методом DFT B3LYP в базисе 6-311G (d,p), мдин/Å.
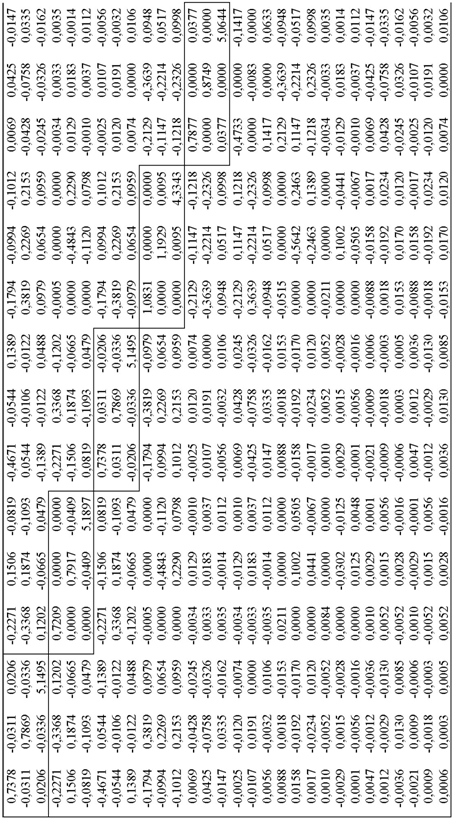
Продолжение таблицы 2.
Свойства субматриц матрицы Fδ0.
Любая матрица Fδ0 может быть представлена в следующем виде:
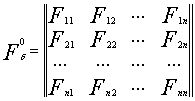
здесь Fij – субматрицы размера 3x3. Причем Fii характеризует i-ую связь, а Fij – взаимодействие i-ой и j-ой связей. Последовательность векторов связей в молекуле пропана следующая (см. рис. 1): 1-2 ,1-3 ,1-4 ,1-5 ,5-6 ,5-7 ,5-8 ,8-9, 8-10, 8-11. Т.о. субматрица F11 в матрице Fδ0 молекулы пропана соответствует связи C-H, обозначенной как 1-2 (см. рис. 1).
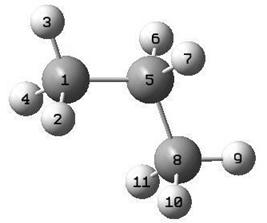
Рис. 1. Молекула C3H8.
Как следует из рис. 1, в молекуле C3H8 имеются 2 эквивалентные связи С-Н, принадлежащие разным СН3-группам (на рисунке это связи 1-3 и 8-9); 2 эквивалентные связи С-Н, принадлежащие группе СН2 (на рисунке это связи 5-6 и 5-7); 4 эквивалентные связи С-Н, принадлежащие разным СН3-группам (на рисунке это связи 1-2, 1-4, 8-10 и 8-11); 2 эквивалентные связи С-С (1-5 и 5-8). Рассмотрим их по-порядку.
2 эквивалентные связи С-Н, принадлежащие разным СН3-группам (на рисунке 1 это связи 1-3 и 8-9), имеют субматрицы F22 и F88 . Отмечается их сходство. При этом диагональные элементы одной субматрицы равны диагональным элементам другой. А элементы, расположенные не на главной диагонали, равны с точностью до знака, что, вероятно, обусловлено симметрией. Самые правые нижние элементы этих субматриц равны вторым производным функции потенциальной энергии по координате z (система координат Xδ0) и соответствуют естественной координате растяжения/сжатия связи C-H.
2 эквивалентные связи С-Н, принадлежащие группе СН2 (на рисунке это связи 5-6 и 5-7) имеют субматрицы F55 и F66 .
4 эквивалентные связи С-Н, принадлежащие разным СН3-группам (на рисунке это связи 1-2, 1-4, 8-10 и 8-11), имеют субматрицы F11 , F33 , F99 и F1010 .
2 эквивалентные связи С-С, имеют субматрицы F44 и F77 .
Как уже было отмечено, самые нижние правые элементы, представленных субматриц, определяют силовые постоянные соответствующих векторов связей. Следовательно, из анализа матрицы Fδ0, следует, что в молекуле пропана силовые постоянные C-H связей лежат в диапазоне 5.06 - 5.19 мдин/Å, а для C-C связи силовая постоянная равна 4.33 мдин/Å. Согласно литературным данным [7], соответствующие значения у углеводородов для C-H связей составляют 4.7 – 5.0 мдин/Å, а для связи C-C - 4.5 – 5.6 мдин/Å.
Элементы, расположенные на главной диагонали рассматриваемых субматриц, соответствующие вторым производным функции потенциальной энергии по координатам x и y (система координат Xδ0), в несколько раз меньше по сравнению с элементами, являющимися вторыми производными по координате z. Заметим, что в координатах Xδ0 каждый вектор связи рассматривается в “своей” системе декартовых координат, и, так как ось z совпадает с вектором связи, то вторые производные функции потенциальной энергии по координатам x и y определяют способность вектора связи менять угол наклона относительно соответствующих осей координат. Значения рассматриваемых величин прекрасно согласуется с общеизвестным фактом, согласно которому деформационные силовые постоянные (в мдин/Å) имеют значения порядка одной десятой от величин валентных силовых постоянных.
Для сравнения матрица силовых коэффициентов в координатах Xδ0 была рассчитана еще одним методом PBEPBE. Следует отметить, что в этой матрице также имеет место сходство субматриц, соответствующих эквивалентным связям. Поскольку отмеченные особенности проявляются в матрицах, рассчитанных различными независимыми методами, можно полагать, что они не являются случайными и имеют закономерный характер. Выявление этих закономерностей является одной из задач дальнейших исследований.
Выводы
Предложен алгоритм ориентации Xδ0 координат, использованный при расчете матриц силовых коэффициентов Fδ0 молекулы пропана.
Установлено, что субматрицы матриц силовых коэффициентов, соответствующих эквивалентным химическим связям, идентичны.
Выявленные характерные особенности силовых постоянных не зависят от способа расчета Fδ0 матриц.
СПИСОК ЛИТЕРАТУРЫ:
1. Mayants L. S., Shaltuper G. B., General methods of analysing molecular vibrations //Journal of Molecular Structure, 24 (1975) P. 409-431.
2. Маянц Л. С., Шалтупер Г.Б. Новый подход к полному расчету колебаний любых молекул// Доклады Академии наук СССР. 1972. Т. 206. № 3. C. 657.
3. Белик А.В., Шляпочников В.А. Квантовохимическая оценка силового поля аммиака в координатах xδ0// Известия Академии наук СССР. 1985 C. 697.
6. Shimanouchi T., Tables of Molecular Vibrational Frequencies Consolidated. Volume I. National Bureau of Standards. 1972. 160. P.
7. Вильсон Е., Дешиус Дж., Кросс П., Теория колебательных спектров молекул. Москва. Издательство иностранной литературы. 1960. 359 с.
Библиографическая ссылка
Савчик Д.В., Белик А.В., Балыкин В.П. ОСОБЕННОСТИ МАТРИЦЫ СИЛОВЫХ КОЭФФИЦИЕНТОВ В КООРДИНАТАХ XΔ0 // Современные проблемы науки и образования. 2008. № 5. ;URL: https://science-education.ru/ru/article/view?id=1118 (дата обращения: 13.01.2026).



