Введение
В современной российской системе образования качество подготовки учащихся по планиметрии неуклонно снижается. Это показывают и результаты ЕГЭ: самая не решаемая четвертая задача уровня С – по планиметрии. Занимаясь с детьми дополнительной подготовкой по математике, можем отметить, что среди сильных детей мало встречаешь любящих геометрию, да и уровень подготовки по геометрии у этих «редких» детей не высокий. В сложившейся ситуации виноваты не дети и не учителя – первопричиной является методика обучения геометрии, определенная политикой государства 60-70 гг. прошлого века.
В решении сложившейся ситуации может помочь такой важный прием обучения планиметрии – построение учащимися точного чертежа. По словам Д. Пойя, «начинающему рекомендуется выполнить большое число чертежей с максимальной точностью, чтобы приобрести для своих знаний хорошую экспериментальную основу: точный чертеж может натолкнуть на открытие геометрической теоремы, даже весьма тонкой» [5, С. 77]. Использование точного чертежа в обучении геометрии позволяет: 1) делать учащимися первые шаги в понимании геометрии как практической науки; 2) постоянно углублять понятие об изучаемой геометрической фигуре (при точном построении возникают вопросы о структуре фигуры, о необходимых и достаточных построениях элементов для получения изображения всей фигуры); 3) осознанно делать первые шаги в выдвижении гипотезы решения геометрической задачи; 4) усиливать значение задач на геометрические построения на плоскости (проводить актуализацию и изучение новых геометрических построений при построении точного чертежа).
В новом веке многие известные методисты, учителя пытаются ответить на вопросы: «Разумно ли изучать геометрию на абстрактном формализованном уровне в отрыве от процессов познания окружающего мира? Приводит ли существующая система изучения геометрии в школе «ум в порядок»? Как же излагают авторы школьных учебников по геометрии доказательства теорем? Как учителя должны учить рассуждать и доказывать на уроках геометрии?» [3]. По нашему мнению, школьная геометрия потеряла свои «корни», руководствуется только аналитическими рассуждениями и оторвана от наглядно-образных представлений учащихся. Современное изложение школьной планиметрии близко к вузовскому и осуществляется по схеме «изложение теоремы и ее применение при решении задач». Известный ученый и популяризатор математики Д. Пойя пишет: «Математика, излагаемая в стиле Евклида, представляется нам систематической, дедуктивной наукой. Но математика в процессе создания является экспериментальной, индуктивной наукой» [5, с. 7].
Так, евклидова геометрия, возникшая из практических нужд человечества, даже в 7 классе не опирается на проведение экспериментальной и практической работы, хотя понятийное мышление учащихся начинает складываться только в старшей школе. Подход учителей в обучении геометрии, основанный на концептуальном подходе традиционных учебных пособий, хорошо отражен в шутке-мнении ученика о первом уроке геометрии: «Учительница странная… нарисовала на доске два равных треугольника и целый урок доказывала, что они равны». Почему в учебнике при изучении признаков равенства треугольников нет задания: «Нарисуйте два различных треугольника, у которых стороны равны 5 и 7 см, а угол между ними 60 °»? На основании этого эксперимента учащиеся не только самостоятельно сформулируют первый признак равенства треугольников, но и увидят его практическую значимость, захотят понять его доказательство. Наблюдение и эксперимент как важнейшие приемы научного познания должны быть постоянными спутниками обучения школьников, но они практически отсутствуют в преподавании геометрии средней и старшей школы. В частности, об этом свидетельствует снижение числа задач на построение циркулем и линейкой в учебниках с 7 по 11 классы. Результат анализа А. В. Белошистой различных современных учебных пособий по геометрии для общеобразовательных учреждений таков: в 7 классе число задач на построение от общего числа задач колеблется от 22 % до 25 %, в 8 классе – 11–14 %, в 9 классе — 5–12 %, в 10 классе – 3–8 %, в 11 классе – 1-3 % [1]. При этом известнейшие геометры-методисты прошлого и современные ученые однозначно признают, что решение задач на построение позволяет значительно поднять качество подготовки учащегося по геометрии.
Серьезным недостатком сложившейся системы обучения планиметрии стало формирование уже в 7 классе «искаженного» принципа зрелого геометра: «Геометрия – это искусство делать правильные выводы по неправильным чертежам». Между тем для детей 7–8 классов в обучении геометрии (как и в содержании учебного пособия для учащихся) основополагающим должен быть другой принцип: «Геометрия – это искусство выдвигать гипотезы решения задачи по нескольким правильным чертежам, далее опровергать или доказывать их».
На уроках геометрии мы говорим детям: «Изобразите геометрический объект в тетради», и дети рисуют, т. е. делают примерное изображение заданного объекта (эскиз), порой даже без линейки. Такое рисование приносит мало пользы для процесса обучения, не несет никакой информации учащимся для решения задачи, более того, еще и приводит к ошибочным выводам. На уроке планиметрии необходимо не «рисовать», а делать геометрический чертеж. Что же такое геометрический чертеж, и какими свойствами он обладает?
Понятие «геометрический чертеж» сложилось в результате развития теории геометрических построений на плоскости. В отличие от черчения, где строятся графические изображения, в геометрии построений на плоскости различными инструментами строятся геометрические образы. Целью теории геометрических построений на плоскости является нахождение алгоритма построения с помощью данных инструментов искомой геометрической фигуры. Нас же интересует максимально точное построение данных фигур и их свойств на плоскости с помощью различных инструментов (циркуля, линейки с делениями, транспортира, угольника и других шаблонов), при этом алгоритм построения не имеет значения. Если задача на доказательство (т.е. в ней доказывается свойство или признак данного объекта), то чертеж должен достаточно точно отражать положение и соотношения элементов изучаемого объекта в самом общем случае. Если задача – метрическая (т.е. в условии даны меры углов, сторон), то необходимо ввести единичный отрезок и изобразить объект с мерами, очень близкими к данным. Не претендуя на причастность к теории геометрических построений, назовем чертеж, обладающий вышеперечисленными свойствами, точным геометрическим чертежом (далее сокращенно «точный чертеж»). Пойя Д. также рекомендует: элементы фигуры не должны быть расположены специальным образом, не указанным в условии задачи; для удобства можно применять жирные, тонкие, разноцветные линии [1].
Построим точные чертежи к трем задачам.
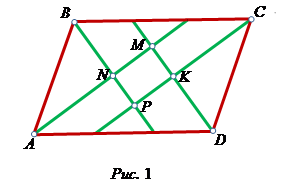
Задача 1. В параллелограмме со сторонами а и b (a > b) проведены биссектрисы внутренних углов. Определите вид четырехугольника, образовавшегося при пересечении биссектрис внутренних углов, и найдите длины его диагоналей.
В соответствии с условием задачи 1 (рис.1) учащиеся увидят очевидное красивое свойство параллелограмма – биссектрисы противоположных углов параллельны. Также учащиеся могут выдвинуть гипотезу, что МКРN – прямоугольник.
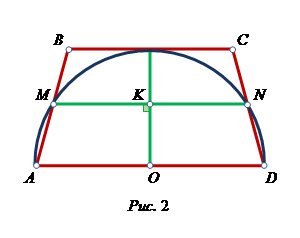
Задача 2. Окружность, построенная на основании AD трапеции ABCD как на диаметре, проходит через середины боковых сторон и касается основания BC. Найдите углы трапеции [4].
Здесь учащиеся столкнутся с несколькими особенностями чертежа (рис. 2): 1) трапеция будет равнобедренной; 2) все построенные трапеции, удовлетворяющие условию задачи, – подобны; 3) высота трапеции – это радиус, перпендикулярный диаметру окружности и делящийся средней линией трапеции пополам.
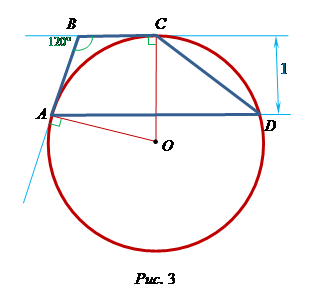
Сложные чертежи к задачам наводят на важный вопрос: как научить ученика выполнять точный чертеж? Покажем это на примере построения следующего чертежа к «трудной» задаче из учебника И. Ф. Шарыгина [6].
Задача 3. В четырехугольнике АВСD стороны ВС и АD параллельны. Точки А, С и D расположены на окружности, касающейся АВ и CВ. Угол АВС равен 120°, а высота треугольника АСD, опущенная на сторону АD, равна 1. Найдите DC [6, С. 127].
Сначала необходимо создать целостное представление о заданной геометрической конструкции в задаче. Для этого необходимо оценить свойства четырехугольника: параллельные стороны четырехугольника находятся на расстоянии 1; угол между сторонами 120°, и эти стороны являются касательными в вершинах треугольника. Тогда построение точного чертежа выполняется следующим образом (рис. 3): 1) строим параллельные прямые а и b на расстоянии 1; 2) откладываем от а угол В, равный 120° в полуплоскость, где находится прямая b; 3) находим точку пересечения А с прямой b; 4) откладываем отрезок BC на а, равный АВ; 5) проводим перпендикуляры из С и А к сторонам угла В, которые пересекутся в точке О – центре данной окружности; 6) строим окружность с центром О и радиусом АО, которая пересечется с b в точке D. При построении точного чертежа становятся «прозрачными» свойства изучаемого геометрического объекта (CO – серединный перпендикуляр к АD; AC = CD; ÐAOC = 60 °), которые приводят к нескольким способам решения задачи.
Как любой инструмент обучения «точный чертеж» имеет определенную область применения. Безмерное использование точных чертежей на уроках может привести к отрицательному результату в обучении планиметрии. Меру использования точных чертежей может понять только учитель. Следует помнить, что «любое количественное изменение выступает как изменение элементов системы» [7], то есть накопление опыта в построении точных чертежей у учащегося приводит к качественному переходу на уровень понятийного мышления (он начнет делать рисунки, которые будут правильно изображать все свойства геометрической фигуры без точных измерений). В этом случае использование точного чертежа необходимо сократить, но не исключить совсем. Поскольку построение точных чертежей не чуждо и математикам при решении отдельных задач в случае, когда понятийное мышление не может решить проблему элементарной планиметрии, аналитически или с использованием эскиза. Поэтому использование точных чертежей актуально не только в 7–8 классах (когда у учащихся не сложилось понятийное мышление в геометрии), но и в 9–11 классах при построении точных чертежей для введения сложных теорем и решения задач уровня выше среднего.
Использование точных чертежей крайне полезно при формировании таких понятий, как «разносторонний треугольник», «разносторонний четырехугольник», «четырехугольник без параллельных сторон», «центр описанной окружности», «вписанный угол», «секущая окружности», «вписанные и описанные многоугольники» и др. Почему даем формулировку «разносторонний треугольник», а не «треугольник»? Попросите детей в классе нарисовать треугольник, четырехугольник, и вы увидите у подавляющего большинства равнобедренные, равносторонние и прямоугольные треугольники, трапеции, параллелограммы и ромбы. Именно эти понятия в процессе обучения планиметрии сформировались в полной мере. Возможно, одной из причин таких построений является стремление к изображению красивой, правильной фигуры. Но этому способствует, например, количество задач с равнобедренным треугольником. Так, в учебнике А. В. Погорелова [2] на закрепление всех трех признаков равенства треугольников предлагается решить 19 задач, а на закрепление понятия «равнобедренный треугольник» – 20. Поэтому неудивительно, что у детей, исходя из опыта решения треугольников, возникает желание понятие «треугольник» подменить красивым и простым понятием «равнобедренный треугольник».
С помощью точного чертежа можно вводить такое важное понятие, как «геометрическое место точек», которое упрощает многие геометрические представления (о серединном перпендикуляре, круге, окружности, центрах описанной и вписанной окружностей, степени точки относительно окружности, преобразовании симметрии, гомотетии и др.). Например, в 7 классе попросить учащихся изобразить на точном чертеже: а) 5 точек, равноудаленных от концов отрезка; б) три точки, равноудаленные от сторон угла; или в) семь точек, равноудаленных от двух параллельных прямых, и т. п. В 8 классе – изобразить ГМТ, из которых отрезок виден под одним и тем же углом, в 9 классе – ГМТ, у которых произведения отрезков секущих относительно двух окружностей равны.
Использование точного чертежа является действенным инструментом мотивации учащихся к изучению планиметрии, анализа геометрической задачи, выдвижения гипотезы ее решения и проверки ее решения. Для этого необходимо использовать точные чертежи в совокупности с проблемным, исследовательским или частично-поисковым методами. Например, учитель делит учащихся на группы и предлагает найти соотношение сторон в прямоугольном треугольнике, т.е. учащиеся должны построить различные точные прямоугольные треугольники, составить в группе таблицу данных по треугольникам и выдвинуть гипотезу о соотношении сторон прямоугольного треугольника.
Не следует забывать об использовании точного чертежа при построении контрпримера. Например, учащиеся часто ошибочно утверждают, что отрезки биссектрис углов треугольника и радиусы вписанной окружности треугольника совпадают. Это заблуждение вытекает, в том числе из-за неверного рисунка, иллюстрирующего построение центра вписанной окружности как точки пересечения внутренних биссектрис треугольника. Точное построение тупоугольного треугольника со сторонами 5, 8, 11 см и его внутренних биссектрис сразу рассеивает заблуждение учащихся.
По нашему мнению, точный чертеж должен стать одним из специфических методов подготовки по геометрии, который позволит гармонично дополнить абстрактно-формализованное содержание и методы обучения планиметрии исследовательскими и экспериментальными формами познания, а также усилить метапредметность геометрического знания.
Рецензенты:
Салехова Ляйля Леонардовна, доктор педагогических наук, профессор, Институт филологии и искусств Казанского (Приволжского) федерального университета, г. Казань.
Шакирова Лилиана Рафиковна, доктор педагогических наук, профессор, Институт математики и механики им. Н. И. Лобачевского Казанского (Приволжского) федерального университета, г. Казань.



