Scientific journal

Modern problems of science and education

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

1. Введение

В различных областях техники широко применяются различного рода теплообменники, в которых, в результате интенсификации теплообмена, может быть достигнуто снижение их массогабаритных показателей при заданных значениях теплового потока, гидравлических потерь, расходов и температур теплоносителей; в ряде случаев задачей является снижение температурного уровня поверхности теплообмена при фиксированных режимных и конструктивных характеристиках. Расчётные методы исследования интенсификации теплообмена при турбулентном течении в трубах разработаны ещё недостаточно. Часто они опираются на упрощённые модели сложных физических явлений, при этом допущения приводят к значительной разнице между расчётными и экспериментальными данными. Экспериментальные данные по теплообмену справедливы только для определённого вида течений и типоразмеров турбулизаторов, на которых были проведены опытные исследования. В связи с этим необходима разработка новых, более точных, чем существующие теоретических методов исследования интенсификации теплообмена при турбулентном течении в трубах. В рамках данного исследования под интенсификацией теплообмена понимаются применение искусственных турбулизаторов потока на поверхности, а также шероховатые поверхности [2, 9]. Модель предполагает двумерную шероховатость. Рассматриваются двумерные поверхности с турбулизаторами, которые применимы и для труб с периодическими диафрагмами.

2. Модель интенсификации теплообмена

Теплообмен при течении в каналах теплоносителей с постоянными теплофизическими свойствами в условиях интенсификации теплообмена моделируется четырёхслойной схемой турбулентного потока [1, 4, 5]. Впервые подобная схема расчёта теплообмена была использована в работах [6-8], а затем существенным образом усложнена в работах [1, 4, 5]. Применим данную модель расчёта теплообмена при турбулентном течении в каналах в условиях интенсификации теплообмена без применения дополнительных допущений, сделанных как в работах [7-9], так и в работах [3-5]. Теперь следует перейти к непосредственному рассмотрению каждого из подслоя.

1. Вязкий подслой. Вязкий подслой располагается в следующей окрестности:

,

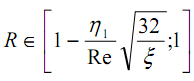где R - безразмерный радиус трубы (отношение расстояния от оси трубы r к радиусу трубы R₀); η₁=5  - постоянная, характеризующая безразмерную толщину вязкого подслоя [1], ξ - коэффициент сопротивления трению. В области вязкого подслоя принимается, что:

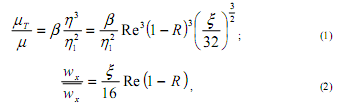
где  - отношение турбулентной и молекулярной динамических вязкостей;

- отношение аксиальной составляющей скорости к среднерасходной;

 - безразмерная координата;

β - постоянная в законе "третьей степени": . [1].

2. Промежуточный подслой. Промежуточный подслой располагается в следующей окрестности:

,

где  [1]. В области промежуточного подслоя принимается, что:

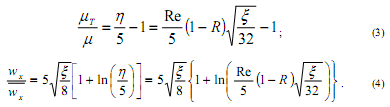
3. Вихревое ядро во впадине. Вихревое ядро во впадине располагается в следующей окрестности:

,

где h - высота турбулизатора. В области вихревого ядра во впадине принимается:

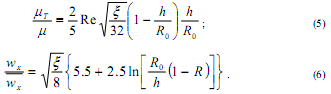
4. Турбулентное ядро. Турбулентное ядро располагается в следующей окрестности: . В области турбулентного ядра принимается:

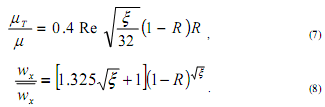
Решение задачи об интенсифицированном теплообмене в данной работе получается с помощью интеграла Лайона:

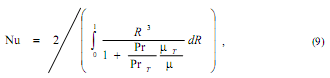
где  - отношение молекулярного и турбулентного чисел Прандтля. В отличие от предыдущих работ ([7-9], а также [3-5]) в рамках данной работы не используется дополнительного допущения о том, что максимальный и средний температурные напоры при интенсифицированном теплообмене соотносятся так же, как и в случае гладкой трубы, т.е. соотношением  (T_w - температура стенки; T_m - максимальная температура потока; - среднемассовая температура потока). Данное допущение является довольно приблизительным, поскольку деформация температурного поля при интенсификации теплообмена довольно значительна. Количественные соотношения, подтверждающие вышеуказанный вывод, приведены в работе [3]. В рамках данной работы удалось избежать этого допущения, поскольку интегрирование производится по безразмерному радиусу, в то время как в работах [3-5, 7-9] - по безразмерной высоте. Точные решения задачи об интенсифицированном теплообмене выглядят следующим образом:

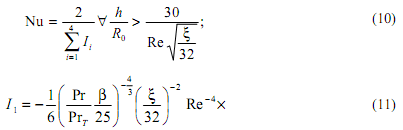
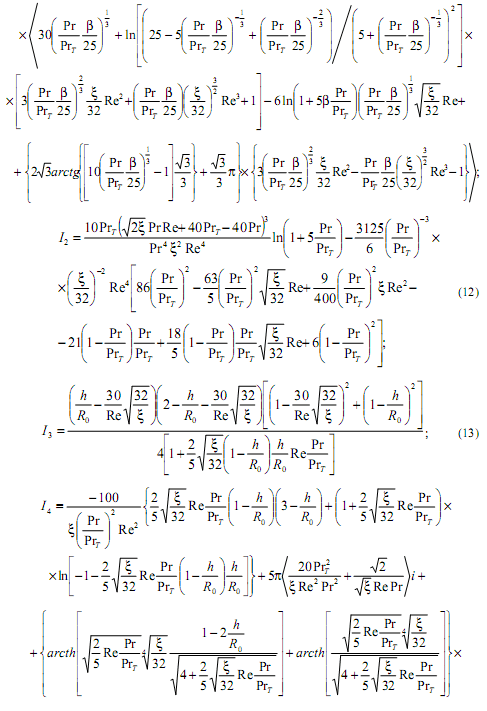
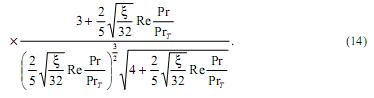
3. Сравнение точного решения задачи об интенсифицированном теплообмене с существующими решениями

Решения Мигая, согласно [7-9], выглядят гораздо проще, чем полученные в данной работе (10)-(14). Очевидно, что точные решения задачи об интенсифицированном теплообмене, представленные в рамках данной работы, гораздо сложнее, чем решения Мигая, что является единственным недостатком первых по отношению к последним. Сравнение результатов расчёта по точным решениям и по решениям Мигая необходимо проводить, сравнивая оба этих решения не только между собой, но и с имеющимися экспериментальными данными. Полученные отношения чисел Нуссельта, рассчитанных по точным решениям Nu, к соответствующим числам Нуссельта, рассчитанных по формулам Мигая Nu^M, в зависимости от числа Рейнольдса при различных числах Прандтля при следующих геометрических параметрах турбулизаторов: t/D=1; d/D=0,90 (t - расстояние между турбулизаторами; d - внутренний диаметр кольцевых канавок; D - внутренний диаметр трубы), показывают, что решение Мигая даёт заниженные результаты относительно точного решения для низких значений числа Прандтля и завышенные для высоких во всём диапазоне чисел Рейнольдса. Для более высоких чисел Рейнольдса это расхождение выше при высоких числах Прандтля и ниже - при низких. Анализ результатов расчётов по точным формулам и по формулам Мигая в зависимости от числа Рейнольдса при прочих равных условиях показывает, что их расхождение может быть довольно значительным - порядка (10¸15)%. Полученные отношения чисел Нуссельта, рассчитанных по точным решениям Nu, к соответствующим числам Нуссельта, рассчитанных по формулам Мигая Nu^M, в зависимости от относительного диаметра трубы с турбулизаторами d/D при различных числах Прандтля при относительном шаге между турбулизаторами t/D=1 и числе Рейнольдса Re=10⁴ показывают, что решение Мигая даёт заниженные результаты относительно точного решения для низких значений числа Прандтля и завышенные для высоких во всём диапазоне относительных диаметров для труб с турбулизаторами. Для более высоких относительных высот турбулизаторов это расхождение выше при высоких числах Прандтля и ниже - при низких. Подробный анализ результатов расчётов по точным формулам и по формулам Мигая в зависимости от относительной высоты между турбулизаторам при прочих равных условиях показывает, что их расхождение может быть довольно значительным - порядка (10¸15)%. После непосредственного сравнения представленных решений между собой, необходимо сравнить эти решения с существующими экспериментальными данными по теплообмену для труб с периодически расположенными поверхностными турбулизаторами [2, 6].

На рис. 1 представлено сравнение точного решения для интенсифицированного теплообмена и решения Мигая с экспериментальными данными [2, 6] для труб с турбулизаторами при t/D=1, Pr=0,72, Re=4·10⁵ в зависимости от относительного диаметра труб с турбулизаторами d/D. Из рис. 1 видно, что точное решение гораздо лучше соответствует существующим экспериментальным данным во всём диапазоне d/D.

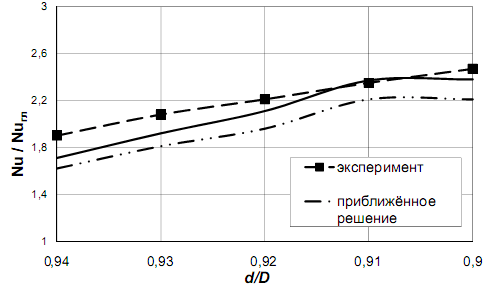
Рис. 1. Сравнение точного и приближённого решений для интенсифицированного теплообмена с экспериментальными данными [2, 6] для труб с турбулизаторами при t/D=1, Pr=0,72, Re=4·105 в зависимости от относительного диаметра труб с турбулизаторами d/D

На рис. 2 представлено аналогичное сравнение, но для при t/D=1, d/D=1, Pr=0,72 и в зависимости от числа Рейнольдса, из которого видно, что точное решение гораздо лучше соответствует существующим экспериментальным данным почти во всём диапазоне чисел Рейнольдса. Подробное расчётное исследование теплообмена в трубах с турбулизаторами посредством точного решения задачи о теплообмене и посредством решений Мигая в диапазоне геометрических параметров турбулизаторов и режимов течения, приведённом в экспериментальном материале [2, 6], показывает, что средняя погрешность расчёта по точными решениям, приведённым в рамках данного исследования, по отношению к эксперименту составляет порядка 5%, в то время как формулы Мигая дают погрешность в среднем более 10%.

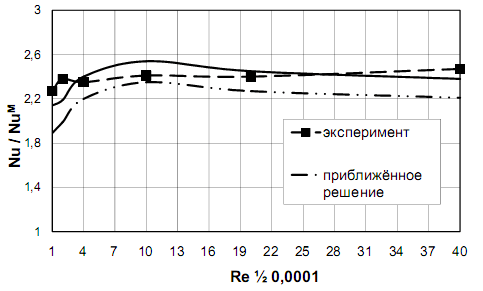
Рис. 2. Сравнение точного и приближённого решений для интенсифицированного теплообмена с экспериментальными данными [2, 6] для труб с турбулизаторами при t/D=1, d/D=1, Pr=0,72 и в зависимости от числа Рейнольдса

Следовательно, точные решения, полученные в данной работе, гораздо качественнее описывают имеющийся экспериментальный материал, что существующие решения. Применение точных решений можно считать оправданным, несмотря на их относительную сложность.

4. Основные выводы

Резюмируя полученные данные, можно сказать, что в рамках данного исследования были получены точные решения задачи об интенсифицированном теплообмене для четырёхслойной схемы турбулентного пограничного слоя. Существующие решения могут быть охарактеризованы как частный случай этих точных решений; точные решения являются более сложными по отношению к существующим решениям. Расчётные данные по теплообмену, полученные с применением точных решений, хорошо соответствуют экспериментальным данным и имеют гораздо меньшую погрешность по отношению к последним, чем существующие решения.

СПИСОК ЛИТЕРАТУРЫ

1. Дрейцер Г.А., Лобанов И.Е. Моделирование изотермического теплообмена при турбулентном течении в каналах в условиях интенсификации теплообмена // Теплоэнергетика. 2003. № 1. С. 54-60.
2. Калинин Э.К., Дрейцер Г.А., Ярхо С.А. Интенсификация теплообмена в каналах. М.: Машиностроение, 1990. 208 с.
3. Кутателадзе С.С. Основы теории теплообмена. М.: Атомиздат, 1979. 416 с.
4. Лобанов И.Е. Математическое моделирование интенсифицированного теплообмена при турбулентном течении в каналах: дисс. ... д.т.н. М.: МАИ, 2005. 632 с.
5. Лобанов И.Е. Моделирование теплообмена и сопротивления при турбулентном течении в каналах теплоносителей в условиях интенсификации теплообмена // Труды Третьей Российской национальной конференции по теплообмену. В 8 томах. Т. 6. Интенсификация теплообмена. Радиационный и сложный теплообмен. М., 2002. С. 140-143.
6. Мигай В.К. Интенсификация конвективного теплообмена в трубах и каналах теплообменного оборудования: дисс. ... д.т.н. Л.: ЦКТИ, 1973. 412 с.
7. Мигай В.К. Моделирование теплообменного энергетического оборудования. - Л.: Энергоатомиздат. Ленинградское отделение, 1987. 263 с.
8. Мигай В.К. Повышение эффективности современных теплообменников. Л.: Энергия. Ленинградское отделение, 1980. 144 с.
9. Эффективные поверхности теплообмена / Э.К. Калинин, Г.А. Дрейцер, И.З. Копп и др. М.: Энергоатомиздат, 1998. 408 с.