Актуальность обозначенной проблемы порождается жизненными и рыночными условиями, в которых педвузам приходится готовить кадры для сферы образования. С одной стороны, контрольные цифры набора по профилю «Математика» ежегодно оказываются в разы ниже потребностей школ в учителях математики, а выпускников – еще меньше. Процесс оптимизации создал ситуацию, когда в некоторых сельских школах вообще некому вести математику: учителя пенсионного возраста уходят, а молодые специалисты неохотно идут преподавать в школу математику. Вот и приходится вузам ежегодно по просьбе органов управления образованием направлять старшекурсников на длительную практику в сельские школы, организуя для них обучение на отдалении. С другой стороны, пандемия весной 2020 года поставила перед вузами задачу в кратчайший срок отправить студентов домой и организовать теперь уже для всех обучение на отдалении. Преподавателям в срочном порядке пришлось адаптировать фонды оценочных средств (ФОСы), созданные для очной формы обучения, к новым условиям.
Организуя образовательный процесс, вузы обязаны заботиться о качестве подготовки выпускника, удовлетворяющей требованиям, заложенным в современных Федеральных государственных образовательных стандартах по направлению «Педагогическое образование» (профиль «Математика») [1], в Концепции непрерывного образования [2]. Среди них на первый план выходит овладение ядром фундаментальных математических знаний, методами научного познания, приемами и средствами их применения в практической деятельности, умениями выстраивать и отслеживать ход своих рассуждений, их аргументации, а также полученные результаты. Необходимость изучать значительную часть программного материала самостоятельно требует усиления внимания к формированию самообразовательной деятельности.
В научно-педагогической литературе достаточно глубоко исследованы: 1) развитие понятия самообразования, выявлены его методологические основы в работах И.Ф. Медведева [3], Ю.В. Сенько, Л.Г. Титовой, В.В. Юдина [4]; 2) проблемы развития профессиональной рефлексии в работах П.Н. Осипова, Т.Е. Седанкиной [5], Л.А. Одинцовой, Л.М. Бронниковой [6] и гармонизации теоретической и практической составляющих в подготовке учителя математики в работах Г.И. Саранцева [7], проблемы отслеживания качества усвоения в работах Сарибейли [8], управления образовательными системами в работах Г.А. Бордовского, А.А. Нестерова, С.Ю. Трапицына [9; 10]. Но до сих пор остаются недостаточно исследованными вопросы организации и создания средств поддержки управления самообразовательной деятельностью обучающихся.
Целью статьи являются: теоретическое обоснование и конструирование дидактического обеспечения управления комплексным очно- дистанционным образовательным процессом по математике, состоящим из выявления структуры, наполнения содержанием каждого компонента; проведение пробной экспериментальной проверки его эффективности.
Материал и методы исследования. Теоретическую базу настоящего исследования составили основные положения: 1) системного и деятельностного подходов в образовании, представленные в работах И.А. Зимней [11], А.В. Хуторского [12] и др.; 2) концепции самообразования, изложенные в работах И.Ф. Медведева [3], Ю.В. Сенько, Л.Г. Титовой, В.В. Юдина [4]; 3) теории гармонизации фундаментальной и практической подготовки будущего учителя математики, нашедшие отражение в работах Г.И. Саранцева [7]; 4) теории управления педагогическими системами, раскрытые в исследованиях Г.А. Бордовского, А.А. Нестерова и С.Ю. Трапицына [9; 10]; 5) основные положения в области развития профессиональной рефлексии в ходе учебно-воспитательного процесса П.Н. Осипова, Т.Е. Седанкиной [5].
Методы исследования: общенаучные (анализ, синтез, абстрагирование, конкретизация, обобщение и систематизация), педагогический эксперимент.
Результаты исследования и их обсуждение. Поясним трактовку основных понятий, используемых в исследовании. Под самообразованием, вслед за И.Ф. Медведевым, будем понимать систематическую целенаправленную исследовательски ориентированную познавательную деятельность, направленную на достижение определенных личностных или социально значимых образовательных целей, управляемую самой личностью [3]. Для нужд настоящего исследования из выделенных И.Ф. Медведевым признаков самообразования [3] акцентируем внимание на следующих: 1) развитая внутренняя мотивация; 2) самостоятельность в деятельности и мышлении, самоактуализация, развивающие непрерывность самообразования; 3) самореализация и саморазвитие; 4) механизмы самоуправления: системность и систематический характер этой деятельности, самонаблюдение и рефлексия, планирование (самоорганизация и самопознание), осуществление (самообучение), самоконтроль и самооценка.
С опорой на Е.С. Полат [13] под дистанционным образованием понимаем такую форму образования, при которой учитель и учащиеся разделены расстоянием, но взаимодействуют путем использования современных информационных и телекоммуникационных технологий. Его характеристики: оперативное обеспечение обучающихся достоверной научной информацией, организация различных видов деятельности обучающихся, активизирующих самостоятельное усвоение знаний и способов деятельности, регулярное и объективное измерение и оценивание результативности обучения с ориентацией на выполнение требований ФГОС, управление образовательной деятельностью студентов и др. Далее будем рассматривать одну из его разновидностей – очно-дистанционную.
Понятие «управление образовательным процессом» будем вслед за Г.А. Бордовским, А.А. Нестеровым и С.Ю. Трапицыным трактовать «...как комплекс средств и способов организации деятельности управляющей и управляемой подсистем, который обеспечивает целенаправленное изменение образовательного процесса с целью придания ему свойств, гарантирующих удовлетворение общественных и личных потребностей и государственных требований по подготовке специалистов заданными показателями качества» [9, с. 17].
С учетом выявленных особенностей управления за основу формирования дидактического обеспечения управления очно-дистанционным образовательным процессом по математике выберем принципы: целенаправленности, системности, деятельности, модульности, гармонизации теоретической и практической составляющих подготовки будущего учителя, рефлексии.
В структуре образовательного процесса функционируют две подсистемы: управляющая – «Преподаватель», и управляемая – «Студенты». Готовясь к его организации, преподаватель, прежде всего, создает рабочую программу дисциплины, очерчивающую ее скелет, который предстоит наполнить конкретным содержанием и подобрать для него формы, средства и методы изложения, четко и доступно отражающие информацию и приемы работы с ней. Указанная деятельность приводит к созданию дидактического обеспечения функционирования образовательного процесса, системообразующим элементом которого выступает – компонент 1. Генеральная цель – управление очно-дистанционным образовательным процессом. Кроме него, в систему дидактического обеспечения входят следующие компоненты: 2. Электронный курс дисциплины (лекционный курс, практические занятия); 3. Комплект заданий для самостоятельной работы (контактной и внеконтактной); 4. Средства поддержки самостоятельной работы (контактной и внеконтактной); 5. Фонд контрольно-оценочных средств; 6. Критерии и показатели овладения знаниями и способами деятельности. Структура дидактического обеспечения управления образовательным процессом изображена на рисунке 1.
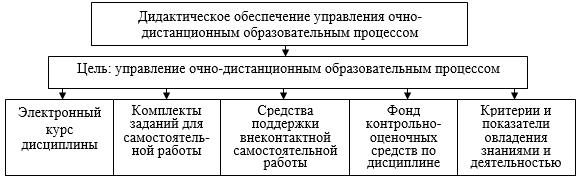
Рис. 1. Структура дидактического обеспечения управления образовательным процессом по математике первокурсников
Итак, обучаясь в педвузе, студент должен подготовиться к осуществлению профессионально-педагогической деятельности: к самостоятельному пополнению и обновлению знаний и способов деятельности в предметной области и методике преподавания; самостоятельной постановке и реализации образовательных целей, формированию содержания, отбору адекватных целям и содержанию форм, методов, технологий, средств организации учебной деятельности обучающихся, выявлять их эффективность и вносить коррективы в организацию образовательного процесса для достижения поставленной цели. Иначе говоря, он должен научиться управлять образовательным процессом. Следовательно, преподаватель должен организовать процесс управления при помощи специально разработанного дидактического обеспечения, показать приемы осуществления управленческих функций, раскрыть природу их цикличности, проиллюстрировать целесообразность использования тех или иных дидактических средств при выполнении различных управленческих функций. Для оперативного управления образовательным процессом (особенно в условиях дистанционного обучения) преподаватель должен предъявить обучающимся содержание учебной информации, четко структурированной, в которой обучающийся смог бы легко ориентироваться. Таким образом, по своей сути второй компонент – содержательный, по форме – это электронный курс дисциплины.
Компонент 2. Электронный курс по дисциплине состоит из двух частей: 1. Электронный курс лекций. Спецификой его являются: а) тщательный отбор теоретического материала, составляющего ядро курса математического анализа, теоретическую базу школьной математики; б) сформированная система примеров, достаточная для конкретизации излагаемого теоретического и практического материала, включающая примеры на аргументацию цепочки утверждений, примеры практического использования изучаемого материала, примеры реализации различных видов рефлексии; 2. Планы практических занятий, включающих вопросы для повторения изученного теоретического материала, выяснение значимости изучаемого в практической деятельности человека; задания на овладение приемами деятельности с изучаемыми математическими понятиями и фактами, приемами построения рассуждений и их аргументации; рефлексивные вопросы и задания на осознание значимости изучаемого материала для будущей профессиональной деятельности.
Компонент 3. Комплекты заданий для самостоятельной работы (контактной и внеконтактной). Материалы этого компонента служат базой для организации самостоятельной деятельности студентов, ориентированной на развитие предметных знаний и способов деятельности (включая самообразовательную) и овладение приемами их использования на практике. Все комплекты заданий распределены по разделам изучаемой дисциплины.
В каждый комплект включены задания следующих типов: 1) на осознание сущности общенаучных методов познания, логических законов и правил построения рассуждений и аргументации утверждений; 2) на формирование и развитие составляющих самообразовательной деятельности; 3) на отбор из заданной совокупности задач тех, которые решаются заданным методом или комбинацией методов, и обоснование выбора; 4) на формирование умений конструировать решение различных типов задач (с избыточным, противоречивым, несформированным условием); 5) на составление по заданной задаче новых задач (аналогичной, обратной, противоположной и др.); 6) на решение задач прикладной направленности, иллюстрирующих практическую значимость изучаемого; 7) на формирование рефлексивной составляющей самообразовательной деятельности с целью развития способности к самоанализу, к прогнозированию результатов своей деятельности; 8) на формирование самоуправленческих умений и навыков: а) осуществление анализа решения задачи; б) планирование деятельности по исправлению обнаруженных ошибок в ходе решения задачи; в) организация деятельности по исправлению обнаруженных ошибок; г) осуществление взаимоконтроля и самоконтроля за результатами деятельности одногруппника и своей собственной деятельности.
Следует заметить, что контактные самостоятельные работы выполняются в аудитории, по объему – небольшие, и трудности, возникающие при их выполнении, можно устранить при помощи преподавателя.
Компонент 4. Средства поддержки внеконтактной самостоятельной работы. Внеконтактная самостоятельная работа выполняется во внеаудиторное время без непосредственного контакта с преподавателем, более объемна, продолжает и дополняет по содержанию контактную. Если внеконтактная работа выполняется на отдалении от преподавателя, у обучающегося могут возникнуть затруднения. Для их устранения она снабжена необходимыми дидактическими средствами поддержки: инструкциями, рекомендациями, гиперссылками с рекомендациями повторить материал или разъяснениями и пр.
Компонент 5. Фонд контрольно-оценочных средств. Компонент включает в себя: 1) перечень всех контрольно-измерительных материалов по дисциплине; 2) систему рефлексивных заданий по каждому контрольному срезу; 3) систему возможных коррекционных заданий для устранения пробелов в усвоении знаний и способов математической деятельности по каждой теме дисциплины.
Компонент 6. Критерии и показатели овладения знаниями и способами деятельности. Компонент предназначен для оценивания результатов выполнения контрольных мероприятий во всех семестрах изучения дисциплины, пролонгированного оценивания достижений обучающегося по дисциплине. Он содержит критерии учебных достижений обучающихся (определяющих степень их соответствия требованиям ФГОС) и конкретизирующие их показатели:
1) мотивационный (целеустремленность, ответственность, четкое следование предъявляемым требованиям, своевременность выполнения заданий);
2) знаниевый (знание и понимание понятий, фактов, приемов и способов деятельности в предметной и методической областях);
3) деятельностно-управленческий (умение и владение приемами и способами математической, рефлексивной и самообразовательной деятельности).
Показатели указанных критериев конкретизируются для каждого контрольного среза. С целью исследования динамики сформированности мотивации, математических знаний и способов математической и управленческой деятельности выделены три уровня (достаточный, средний и высокий), приведены характеристики по выделенным показателям.
Предлагаемое дидактическое обеспечение управления очно-дистанционной образовательной деятельностью первокурсников прошло годичную пробную экспериментальную проверку в преподавании математического анализа в рамках одного вуза. В первом полугодии электронные ресурсы дидактического обеспечения использовались в условиях очного обучения для организации самостоятельной внеконтактной работы и ее контроля. Во втором полугодии – помогли организовать дистанционный образовательный процесс, установить оперативную обратную связь, своевременно оказывать необходимую помощь студентам в выполнении заданий, их анализа, коррекционной работы и оценивания результатов самостоятельного изучения дисциплины.
Структура управления образовательным процессом представлена схематично на рис. 2.
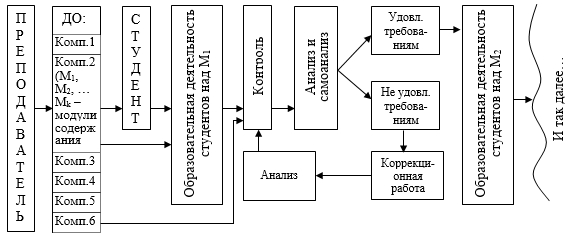
Рис. 2. Структура управления очно-дистанционным образовательным процессом
В ходе пробного этапа проверки эффективности функционирования дидактического обеспечения управления очно-дистанционным образовательным процессом по математике в экспериментальной группе первого курса осуществлены: 1) проверка эффективности отбора учебного содержания, последовательности, методов и средств его предъявления обучающимся, используемых способов управления образовательным процессом на основе созданных средств дидактической поддержки; 2) отслеживание сформированности знаний, самообразовательной деятельности в ходе образовательного процесса; 3) проведение и сравнение результатов входного (сентябрь 2019 г.) и итогового (июнь 2020 г.) контроля на основе критериального аппарата с помощью метода углового преобразования Фишера, показавшего положительные сдвиги в усвоении знаний и деятельности первокурсников.
Выводы. В настоящей статье с опорой на концептуальные основы самообразования и организации дистанционного обучения выстроено теоретическое обоснование необходимости управления процессом очно-дистанционного обучения и создания дидактического инструментария, обеспечивающего успешность реализации всех функциональных компонентов управленческого цикла. На базе системного и деятельностного подходов разработаны структура и содержание дидактического обеспечения управления очно-дистанционным образовательным процессом подготовки будущего учителя математики. Выяснены педагогические условия его эффективности: 1) организация усвоения математических знаний и деятельности на основе мотивации и гармоничного сочетания теоретической и практической составляющих подготовки будущего учителя математики; 2) организация непрерывной рефлексивной деятельности в процессе изучения любой математической дисциплины; 3) формирование и непрерывное использование критериального аппарата усвоения математических знаний и способов деятельности.



