Как известно, одна из наиболее важных задач школьного курса геометрии – развитие логического мышления обучающихся. Логические переходы при решении геометрических задач и применяемые в геометрии правила их использования способствуют стойкому формированию умений обоснования и доказательства различных суждений. Кроме этого, процесс оперирования точными геометрическими определениями и теоремами также развивает логическую интуицию, позволяет наглядно продемонстрировать механизм логических построений и помогает освоить их применение учениками.
В итоге геометрия занимает одно из ведущих мест в формировании логического мышления школьников, поскольку ни одна другая школьная дисциплина так планомерно не развивает этот вид мышления. Помимо всего, изучение геометрии развивает воображение школьников, существенно обогащает и развивает их пространственные представления.
Умение решать геометрические задачи всегда считалось признаком хорошо развитой логики. В наше время данное умение также играет очень важную роль, поскольку хорошо развитое логическое мышление необходимо на практике, во многих профессиональных сферах деятельности человека и в его повседневной жизни.
Стоит подчеркнуть, что практически не существует такой отрасли жизни человека, где бы не требовалось использование навыков мышления с использованием логики. Это относится не только к применению знаний из технических наук, гуманитарные науки также используют различные логические конструкции.
Цель исследования. Использование логики позволяет ускорить процесс мышления, повышает его качество, помогает более грамотно изложить свои мысли, сделать достоверные выводы и избежать ложных рассуждений. И здесь очень важна роль геометрии. Для улучшения геометрической подготовки выпускников общеобразовательной школы предлагается сочетание индивидуализации и многовариантности методов решения заданий.
Материал и методы исследования. В общепринятой литературе по психологии принято подразделение логического мышления человека на четыре составные части: наглядно-действенное, конкретно-предметное, наглядно-образное и абстрактно-логическое [1].
В методике обучения геометрии наибольший интерес представляет наглядно-образное и абстрактно-логическое мышление. При рождении у человека нет задатков грамотно делать выводы из различных ситуаций или строить правильные логические конструкции, поскольку логическое мышление – не врожденное, а приобретенное им свойство. Даже конкретно-предметное мышление проявляется у детей начиная с 1,5 лет. Умение же мыслить абстрактно появляется еще позже – с началом обучения в школе, примерно в 7-8 лет. В результате в процессе развития личности ребенка постепенно развивается и его логика, при этом планомерные регулярные тренировки и упражнения дадут только стойкий положительный результат в развитии логического мышления.
На важную роль геометрии в развитии логического мышления указывали многие специалисты в области математики и методики ее преподавания. Так, Герман Вейль писал: «Логика – это своего рода гигиена, позволяющая математику сохранять свои идеи здоровыми и сильными» [2].
В своей методике геометрии [3] Н.М. Бескин, автор известных советских учебников, выделяет три цели преподавания геометрии:
1) сообщение геометрических сведений (знания геометрии необходимы при изучении других предметов и будут нужны в профессиональной деятельности);
2) логическое развитие (не логика в чистом виде, а лишь применение логических приемов в курсе геометрии);
3) развитие пространственного воображения (достижение его предлагается путем решения задач на построение).
Еще один известный советский математик В.М. Брадис в своем методическом руководстве [4] констатирует, что основная цель изучения геометрии – овладение основами этой науки, при этом подчеркивается: залог успешного изучения геометрии – это гармоничное развитие пространственного воображения, логического мышления и выработки навыков в практических приложениях.
Определяя наиболее важные цели преподавания геометрии, один из авторов учебника по углубленному изучению геометрии для средней школы А.Д. Александров [5] указывает на уникальность геометрии, которая выделяет ее из списка не только дисциплин математического профиля, но и всех наук в целом, и заключается в сплетении строгой логики обоснования теоретических и практических положений с их наглядным представлением. Таким образом, геометрия связывает живое воображение со строгой логикой, что взаимно дополняет их.
С другой стороны, с развитием технического прогресса появляются новые области пространственных восприятий (например, виртуальные и многомерные пространства, цифровые технологии и т.д.), при этом коренным образом меняются технологии разнообразных производств, что приводит к необходимости изменения не только целей обучения геометрии, но и всего школьного геометрического образования. Однако, несмотря на все эти изменения, основные положения самой науки геометрии продолжают сохраняться на прежнем уровне, что приводит к проблеме их развития и приведения к уровню, актуальному на данном этапе развития общества и производства.
Во все времена общество, в соответствии с уровнем своего развития, ставило перед образованием подрастающего поколения конкретные цели обучения, которые соответствовали общественным запросам. В настоящее время к курсу на получение высшего образования добавилась цель индивидуализации обучения, которая предполагает не только максимальное выявление способностей и возможностей обучаемых, но и приобретение ими соответствующих компетенций (так называемый компетентностный подход). В результате успех в достижении последней цели геометрического образования напрямую стал зависеть, с одной стороны, от задатков и врожденных способностей человека, от влияния их развития на получение образования, в том числе геометрического, а с другой – от возможности их развития посредством изучения геометрии [6].
Рассмотрим различные интерпретации понятия «индивидуализация» в современной педагогической литературе.
В педагогической энциклопедии [7] индивидуализация определяется как организация учебного процесса, при котором выбор способов, приемов, темпа обучения учитывает индивидуальные различия учащихся, уровень развития их способностей к обучению.
В широко известной в начале 90-х годов ХХ века работе [8] И.Э. Унт трактует индивидуализацию как учет в процессе обучения индивидуальных особенностей учащихся во всех его формах и методах независимо от того, какие особенности и в какой мере учитываются.
Индивидуальный подход – ориентация на индивидуально-психологические особенности учеников, включение в работу с ними специальных способов и приемов, соответствующих их индивидуальным особенностям [9].
Результаты исследования и их обсуждение. Подведение итогов обзора мнений различных авторов по вопросу индивидуализации обучения школьников приводит к логичному вопросу: как же при обучении геометрии в наибольшей степени развить образно-логическое мышление, учитывая индивидуальные особенности учащихся? Для этого должна быть разработана специально продуманная система заданий, методов и приемов, а также учтены психологические типы индивидуумов. Этим и обусловлена актуальность данной статьи.
Конечно, решению данной проблемы можно посвятить большое исследование. Поскольку мы ограничены рамками статьи, то рассмотрим лишь небольшой прием, который позволяет развить творческие и логические способности учащихся, с учетом их индивидуальных особенностей, при подготовке к ОГЭ и особенно ЕГЭ.
Речь пойдет о решении планиметрических задач из материалов для подготовки к ЕГЭ, поскольку на уроках геометрии в 10-11 классах решаются задачи по стереометрии, где не в полной мере повторяются многие более или менее известные формулы и теоремы из планиметрии. Это – те формулы и теоремы, которым в учебнике по геометрии до 9 класса уделено немного внимания и задач на их применение мало или они не имеют практического приложения.
Для работы с сильными учащимися на уроках геометрии предлагаем следующий методический прием: нескольким учащимся примерно одинакового уровня подготовки предлагается одна и та же задача, при этом на первом этапе работы каждому из учеников предлагается решить задачу определенным способом или по конкретной формуле. После выполнения задания ответы сверяются и индивидуальные приемы решения обсуждаются вместе со всем классом с выбором наиболее рационального. При этом важно разобрать и не совсем удачные решения, потому что, как утверждал Д. Пойа, «при решении задачи плохой план часто оказывается полезным: он может вести к лучшему плану» [2]. Если класс достаточно слабый, то подобную работу можно проводить на факультативах или кружках.
На следующем этапе работы в данном направлении одинаковая задача предлагается для решения нескольким ученикам, причем все подсказанные учителем методы или формулы группа учеников распределяет самостоятельно. Обсуждение решения проводится коллективно, при этом каждый из выполнявших решение должен доказать, что его метод наиболее рационален, краток и изящен. Понятие красивого решения задачи встречается на уроках все реже, а жаль. Ведь рациональность решения задания не является самоцелью, а позволяет показать детям, что сложную проблему иногда можно решить очень просто, затратив минимум времени.
В дальнейшем подобная работа предлагается уже без указания способа решения, но одна задача опять предлагается для группы из 3-4 человек. Таким образом, дети должны вначале обсудить все возможные методы решения задачи, затем распределить между собой кто и каким методом будет ее решать, в конце решения сверить ответы. При таком приеме уже один из участников группы будет проводить анализ возможных способов решения задачи у доски с выделением наиболее интересных и рациональных методов.
Регулярное применение таких методических приемов, начиная с 8-9 классов, когда ученики уже узнают достаточное количество формул и методов решения геометрических задач, позволит к окончанию 9 класса подвести наиболее сильную часть учащихся к такому уровню, который поможет им в дальнейшем более органично перейти к изучению стереометрии. Кроме этого, такая методика позволяет подготовить детей к рациональному решению планиметрической задачи №16 из второй части профильного ЕГЭ, которая традиционно вызывает наибольшие затруднения при решении, как показывает статистика сдачи указанного экзамена.
Рассмотрим на примере одной из задач, как можно организовать решение и обсуждение возможных альтернативных планов ее решения.
Задача. Основания трапеции равны 10 и 5, а диагонали – 9 и 12. Найти площадь трапеции.
1 способ (с применением теоремы Пифагора).
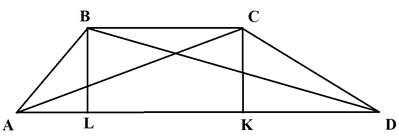
Проведем две высоты данной трапеции к стороне AD. Тогда LK=BC=5, следовательно, AL+KD=5. Пусть AL=x, тогда KD=5-x. Из треугольника BLD по теореме Пифагора получим BL2=122–(10–x)2. Аналогично из треугольника ACK: CK2=92–(5+x)2. Так как BL=CK, как высоты одной трапеции, проведенные к одной и той же стороне, то получим уравнение:
122–(10–x)2=92–(5+x)2,
144–(100–20х+х2)=81–(25+10х+х2),
144–100+20х=81–25–10х,
30х=81–25–144+100,
30х=12, х=0,4.
Значит, CK2=92–(5+0,4)2, CK2=81–29,16=51,84, CK=7,2. Окончательно получаем, что площадь трапеции равна: S=(5+10)/2*7,2=54 кв. ед.
Ответ: 54 кв. ед.
2 способ (с помощью дополнительных построений).
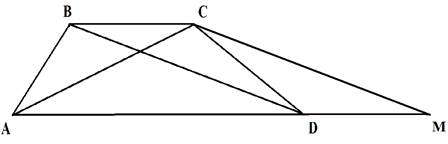
Дополнительное построение: CMǁDB. Тогда DM=5, AM=15. Площадь полученного треугольника ACM равна площади исходной трапеции ABCD (этот факт можно отдельно доказать и в дальнейшем использовать при решении задач). Найдем эту площадь по формуле Герона. Полупериметр равен:
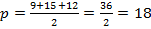 .
.
Тогда площадь равна: 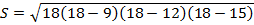 ,
,
 ,
,
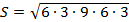 ,
,
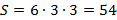 .
.
Ответ: 54 кв. ед.
3 способ (с помощью подобия треугольников).
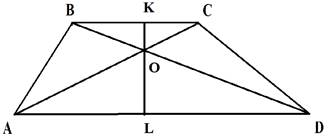
Проведем высоту трапеции KL через точку пересечения диагоналей O. Тогда высота трапеции равна сумме KO+LO. 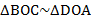 (по двум углам)
(по двум углам)
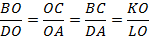
Пусть 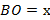 ,
, 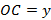 , тогда
, тогда 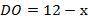 ,
, 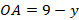 . Получим два уравнения:
. Получим два уравнения: 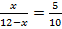 и
и 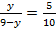 . Откуда x=4 и y=3. Найдем высоту KO треугольника BOC из двух формул площади треугольника: Герона и формулы с высотой. Получаем:
. Откуда x=4 и y=3. Найдем высоту KO треугольника BOC из двух формул площади треугольника: Герона и формулы с высотой. Получаем: 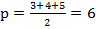 ,
, 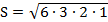 =6,
=6, 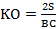 ,
, 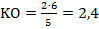 , значит LO=2KO=4,8, и вся высота KL=7,2. Тогда площадь трапеции равна: S=(5+10)/2*7,2=54 кв. ед.
, значит LO=2KO=4,8, и вся высота KL=7,2. Тогда площадь трапеции равна: S=(5+10)/2*7,2=54 кв. ед.
Ответ: 54 кв. ед.
Проводя анализ вышеизложенных методов решения задачи, стоит обратить внимание учеников на то, что все три приема решения геометрической задачи в данном случае будут в дальнейшем активно применяться при решении других задач. Наиболее «красивым» является метод с дополнительным построением, который вызывает у детей наибольшие трудности именно из-за сложности видения этого дополнительного построения. В этом методе стоит подчеркнуть, что построение диагонали трапеции (или параллелограмма), параллельной одной из двух данных, приводит к образованию треугольника, площадь которого равна площади исходной трапеции, что также в дальнейшем может использоваться при решении задач. Это послужит пропедевтикой к изучению следующих тем.
Заключение. Хочется подчеркнуть, что с каждым годом уровень школьного геометрического образования в нашей стране, к сожалению, падает, и в этом свою отрицательную роль играет, как ни странно, проведение ЕГЭ. Многие учителя, стремясь лучше подготовить своих подопечных к хорошей сдаче экзамена, концентрируют свое внимание на алгебре в ущерб урокам геометрии, да и малое количество часов, отводимых на изучение геометрического материала, не позволяет дать качественную геометрическую подготовку выпускникам. В этой ситуации на помощь и придет описанный выше метод работы с сильными учащимися, позволяющий учитывать их индивидуальные особенности.



