Согласно Концепции развития математического образования в Российской Федерации «математика занимает особое место в науке, культуре и общественной жизни, являясь одной из важнейших составляющих мирового научно-технического прогресса» [1]. Без высокого уровня математического образования невозможно выполнение поставленной задачи по созданию инновационной экономики в нашей стране.
На повышение качества образования, обновление его содержания, подготовку соответствующих профессиональных кадров, их переподготовку и повышение квалификации нацеливает нас и национальный проект «Образование».
Проблема совершенствования содержания, методов, форм и средств обучения математическим дисциплинам в высшей школе обсуждалась и раньше, однако в условиях введения новых федеральных государственных образовательных стандартов (ФГОС) она стала особенно актуальной. Это вызвано рядом причин: появлением двух уровней высшего образования: бакалавриата и магистратуры; сокращением количества часов на изучение фундаментальных математических дисциплин, особенно в условиях бакалавриата; увеличением доли самостоятельной работы студентов в учебном процессе и т.д. В связи с этим возникла острая необходимость разработки учебных пособий для студентов, отвечающих новым требованиям: компетентностному подходу в образовании, усилению практико-ориентированной направленности обучения, организации эффективной самостоятельной работы студентов в образовательном процессе вуза.
В ФГОС высшего образования сегодня заявлена компетентностная модель образования, определены два вида компетенций – общие и профессиональные. Для формирования этих компетенций студенту педагогического вуза профиля «Математика» и совмещенных с ним профилей необходимо овладеть содержанием ряда учебных дисциплин, среди которых математическим дисциплинам принадлежит ведущая роль.
В системе математического образования вуза одной из фундаментальных дисциплин является математический анализ. В задачи этой дисциплины входит не только усвоение студентами понятий, теорем и методов их доказательства, овладение методами решения задач, но и развитие их логического мышления и математической культуры, необходимых для дальнейшего изучения математики и других дисциплин, для практической деятельности.
В педагогическом вузе роль этой дисциплины обусловлена ещё и тем, что элементы математического анализа изучаются в школе. Поэтому понимание и усвоение базовых понятий математического анализа, их свойств и умений оперировать ими в разных ситуациях очень важно для будущего учителя математики. Кроме того, математический анализ имеет большое общеобразовательное и прикладное значение, многие вопросы содержат материал, способствующий формированию научного мировоззрения студентов.
Базовая математическая подготовка будущего учителя математики является основой его профессиональной деятельности, так как именно математические знания обеспечивают ему высокий уровень математической компетентности, возможность осваивать новые приемы и методы обучения. Однако наряду с математическими знаниями и умениями учитель должен обладать и определенными методическими умениями, позволяющими ему разрабатывать свои методики и технологии обучения понятиям, фактам, выстраивать индивидуальные образовательные траектории учеников, руководить их проектной, поисково-исследовательской деятельностью и т.д.
Сегодня во всех сферах, в том числе и в области образования, все больше востребованы специалисты, обладающие практико-ориентированными компетенциями, способные к профессиональному саморазвитию и самосовершенствованию. В ФГОС высшего образования эта особенность проявляется как ориентация на «результаты обучения», которые отражаются в совокупности общекультурных и профессиональных компетенций. В этой связи обязательным элементом системы математического образования в педвузе становятся практико-ориентированные формы организации занятий или создание на занятиях практико-ориентированных ситуаций.
Цель исследования – выделить основные направления практико-ориентированного обучения математическому анализу студентов педвуза и раскрыть методику реализации этих направлений на практике.
Материал и методы исследования. В качестве материала исследования были использованы: ФГОС высшего образования и содержание дисциплины «Математический анализ» по направлению «Педагогическое образование». В ходе исследования был проведен анализ педагогической и научно-методической литературы, вузовских учебников по математическому анализу, школьных учебников, материалов ЕГЭ, интернет-источников; проводились: наблюдение, беседы, эксперимент; анализировался многолетний личный опыт преподавания математического анализа в педагогическом вузе.
Результаты исследования и их обсуждение. Проблеме практико-ориентированного обучения посвятили свои работы известные отечественные ученые, педагоги и методисты: А.А. Вербицкий [2], Б.С. Гершунский [3], М.В. Егупова [4], Н.Н. Дербеденева [5], Л.Р. Загитова [6], Л.А. Одинцова [7], Г.И. Саранцев [8; 9], Ф.Г. Ялалов [10] и др. Профессионально-педагогическая направленность специальной подготовки учителя математики была исследована в докторской диссертации профессора А.Г. Мордковича (1986). Анализ трудов этих авторов показал, что практико-ориентированное обучение рассматривается сегодня как процесс освоения обучающимися образовательной программы с целью получения практических знаний, умений и навыков, необходимых в профессиональной среде. Иначе говоря, практико-ориентированное обучение – это вид обучения, в процессе которого происходит формирование и развитие профессиональных компетенций студентов.
Цель практико-ориентированного обучения заключается в том, чтобы помочь студенту «открыть» и применить полученные теоретические знания, научиться самостоятельно решать проблемы, адаптироваться к профессии в современных условиях.
Практико-ориентированная направленность обучения математическому анализу в педвузе предполагает формирование у студентов методических умений неразрывно с предметными умениями. К предметным или специфическим умениям в курсе математического анализа относятся, например, умения вычислять пределы последовательностей и функций, находить производную или интеграл от функции одной и многих переменных, исследовать ряды на сходимость и др.
Кроме этих умений (действий), есть действия, которые носят общеучебный и общепознавательный характер и применяются при изучении разных дисциплин, такие как анализ и синтез, сравнение и аналогия, доказательство и опровержение, подведение под понятие и др. Формирование этих умений происходит в процессе освоения конкретного учебного материала. Все они используются учителем на практике для организации активной познавательной деятельности школьников, поэтому их также относят к методическим умениям. Математический анализ предоставляет большие возможности для формирования подобных методических умений в единстве с предметными умениями.
Таким образом, учитывая вышесказанное, можно выделить следующие основные направления практико-ориентированного обучения математическому анализу студентов направления подготовки «Педагогическое образование».
I. Обучение анализу математических объектов и условий, в которых они заданы
К математическим объектам, которые изучаются в курсе математического анализа, мы относим: числовые и функциональные последовательности, функции одной и многих переменных, пределы последовательностей и функций, производные и дифференциалы функций одной и многих переменных, неопределенный и определенный интегралы от функций одной переменной, числовые и функциональные ряды и т.д. Приведем примеры.
Пример 1. Если поставлена задача: найти производную функции, то сначала студент должен провести анализ данной функции, то есть ответить на вопросы:
1) Какая это функция, простая или сложная?
2) К какому типу она принадлежит (степенным, показательным, логарифмическим, тригонометрическим, гиперболическим и т.д.)?
3) Какие способы вычисления производной данного вида функций мне известны, и какой из них наиболее рациональный?
4) Какие действия необходимо выполнить для реализации этого способа?
5) Можно ли найти производную другим способом? И т. д.
Пример 2. Если ставится задача исследовать ряд на сходимость, то студент должен сначала провести анализ этого ряда, то есть ответить на вопросы:
1) Какой это ряд, числовой или функциональный?
2) Если это числовой ряд, то какой он, положительный или знакочередующийся?
3) Какой признак сходимости следует применить в данных условиях и почему?
4) Какие действия необходимо выполнить для реализации выбранного признака?
5) Можно ли исследовать сходимость данного ряда другим способом?
В случае применения признака сравнения для положительного ряда студент должен ещё высказать гипотезу: сходится ряд или расходится, и в зависимости от этого искать для данного ряда мажоранту (ряд с большими членами) или миноранту (ряд с меньшими членами), а затем провести сравнение двух рядов и сделать вывод о сходимости исходного ряда.
Такая система работы позволяет закрепить в сознании студента определенную схему анализа заданной математической или иной информации и систему вопросов, которые он может затем применять в своей профессиональной деятельности при решении задач или возникающих проблем. Действия и операции, которые многократно выполняет студент в ходе практико-ориентированного обучения, интериоризируются с тем, чтобы вновь реализоваться во вне, уже в новых условиях.
II. Создание ситуаций «открытия» нового знания
Математический анализ изучается на первых курсах вуза, и студенты, как показывает практика, испытывают значительные трудности, связанные с усвоением понятий, теорем и методов решения задач этой дисциплины. Математический анализ отличают высокая степень абстрактности изучаемого материала и насыщенность его символическим языком. Такая особенность содержания курса является его спецификой, поэтому полностью исключить её невозможно, однако можно нейтрализовать негативные стороны этого явления за счет более полного использования геометрической наглядности и включения самих студентов в «открытие» нового знания, в активную познавательную деятельность.
Анализ содержания дисциплины «Математический анализ» в вузе показал, что многие понятия и теоремы этого курса допускают обобщение и аналогию. Например, обобщение можно использовать при изучении следующих понятий:

Аналогия будет полезна при изучении следующих понятий и теорем:

Такие цепочки обобщений, аналогичных понятий и теорем математического анализа можно составить, опираясь на содержание изучаемой дисциплины.
Используя в обучении аналогию, обобщение, мы создаем ситуации «открытия» нового знания. Студенты при этом приобретают умения и опыт, которые они могут использовать в дальнейшем в своей практической деятельности.
К практико-ориентированным ситуациям, которые целесообразно создавать на лекционных и практических занятиях по математическому анализу и которые ориентированы на формирование методических умений будущих педагогов, можно отнести следующие.
Ситуация 1. Студентам предлагается сформулировать определение понятия или содержание теоремы сначала на естественном языке, затем записать аналитически (буквенно-символически) и дать геометрическую интерпретацию этого понятия или теоремы, например:
1. Сформулируйте определение предела последовательности, запишите его символически и дайте геометрическую интерпретацию.
2. Сформулируйте свойства определенного интеграла, запишите их символически и дайте геометрическую интерпретацию.
3. Сформулируйте теорему о среднем, запишите её символически и дайте геометрическую интерпретацию, сделайте чертеж.
Ситуация 2. Студентам дается задание: сформулировать теорему, обратную данной, и установить её истинность или ложность. Например, после изучения теоремы, выражающей связь дифференцируемости и непрерывности - «Если функция дифференцируема в некоторой точке, то она и непрерывна в этой точке», дается задание: сформулировать теорему, обратную данной, и установить её истинность или ложность.
Аналогичное задание можно предложить и после изучения теоремы «Если числовой ряд сходится, то n-й член ряда стремится к нулю при 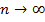 ».
».
Ситуация 3. Студентам предлагается сформулировать теорему, которая выражает необходимое условие, а затем сформулировать обратное утверждение и проверить, выражает ли оно достаточное условие. Возможно и обратное: сначала сформулировать утверждение, выражающее достаточное условие, а затем обратное ему и установить, является ли оно необходимым условием. Такие ситуации можно создать, например, при изучении экстремума функции, выпуклости и точки перегиба, сходимости числового ряда и т.д.
Ситуация 4. После введения нового метода решения задач студентам предлагается выделить действия, составляющие данный метод, и составить алгоритм или алгоритмическую схему данного метода.
Ситуация 5. Студентам дается задание решить задачу разными способами и выбрать из них наиболее рациональный. Математический анализ предоставляет здесь особенно много возможностей при вычислении пределов, производных, интегралов, площадей, объемов, исследовании рядов на сходимость или равномерную сходимость и т.д.
Ситуация 6. Студентам предлагается подготовить историческую справку, выступить с сообщением по теме, создать презентацию к докладу.
Большие возможности математический анализ предоставляет для развития творческого мышления и формирования поисково-исследовательских умений студентов. В процессе обучения этой дисциплине они могут получить опыт организации поисково-исследовательской деятельности, необходимый в их профессиональной деятельности для подготовки школьников к участию в разных конкурсах, форумах, олимпиадах. Отсюда получаем новое направление практико-ориентированного обучения.
III. Организация поисково-исследовательской деятельности студентов и формирование у них поисково-исследовательских умений
Поисковая деятельность трактуется как вид познавательной деятельности, направленной на решение проблемных задач. Исследовательскую деятельность в методике обучения математике понимают как «творческую деятельность, продуктом которой являются новые знания» [11, с. 105]. Поисково-исследовательская деятельность включает действия как поисковой, так и исследовательской деятельностей.
Поисково-исследовательскую деятельность студентов при обучении математическому анализу можно организовать с помощью серии задач, первая из которых поисковая (проблемная), и одна или две общего вида (исследовательского характера). Приведем примеры.
Пример 1. Найти производную 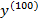 , если
, если 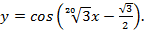
Проведя анализ содержания задачи, студенты делают вывод, что её можно решить поэтапно, последовательно вычисляя производные, но это приведет к некоторым вычислительным трудностям. Поэтому возникает мысль сформулировать сначала задачу в общем виде, заменив числовые коэффициенты буквенными, и решить её. Таким образом, возникает проблема: найти 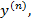 если
если 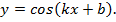
Вычислив первые четыре производные, студенты замечают закономерность. Используя полученные результаты, они находят решение данной задачи.
Пример 2. Найти неопределенный интеграл 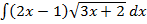 [12, с. 413].
[12, с. 413].
Студенты замечают, что интеграл можно вычислить разными способами: методом подстановки или методом интегрирования по частям. Затем им предлагается сформулировать задачу более общего вида. Заменив в подынтегральной функции числовые коэффициенты буквенными, а также линейный множитель квадратным трехчленом, они получают две проблемы:
Проблема 1. Найти неопределенный интеграл вида
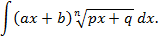
Проблема 2. Найти неопределенный интеграл вида
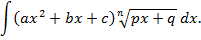
Найти решения этих проблем помогает решение первой задачи.
Пример 3. Составить уравнение общей касательной к графикам функций
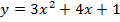 и
и 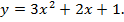
Эту задачу можно решить несколькими способами. Если заменить в ней числовые коэффициенты буквенными, то возникает проблема: «Составить уравнение общей касательной к графикам функций 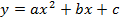 и
и 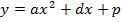 ». Для её решения необходимо решить сначала несколько «частных» задач разными способами, выбрать из них наиболее рациональный и найти зависимость между параметрами.
». Для её решения необходимо решить сначала несколько «частных» задач разными способами, выбрать из них наиболее рациональный и найти зависимость между параметрами.
Кроме заданий, приведенных выше, поисково-исследовательский характер имеют и задания следующего типа.
Пример 4. Пользуясь определениями четной и нечетной функций, докажите:
1) сумма или разность двух четных (нечетных) функций есть четная (нечетная) функция;
2) произведение (частное) двух одинаковых по четности функций есть четная функция;
3) произведение (частное) двух разных по четности функций есть нечетная функция;
4) композиция двух функций одинаковой четности есть функция той же четности;
5) композиция двух функций разной четности есть функция четная.
Можно также предложить студентам обобщить эти свойства, а затем доказать их:
1) алгебраическая сумма конечного числа функций одинаковой четности есть функция той же четности;
2) произведение конечного числа четных функций есть четная функция;
3) произведение четного числа нечетных функций есть четная функция;
4) произведение нечетного числа нечетных функций нечетная функция.
Кроме рассмотренных, есть много других примеров, которые помогают организовать поисково-исследовательскую деятельность студентов в процессе обучения математическому анализу. Такую работу можно организовать не только индивидуально, но и в малых группах или со студентами всей группы. Например, можно провести математическую деловую игру по теме «Сходимость числовых рядов». Студенты группы разделяются на несколько малых групп по 4-5 человек. В группе по определенным правилам распределяются роли. Каждой группе предлагается задание: исследовать числовые ряды на сходимость. Члены группы совместно решают поставленную проблему, выполняя свои роли. Затем от каждой группы выступает докладчик с результатами выполнения задания. Остальные студенты слушают, задают вопросы, дополняют. В конце игры подводятся итоги, выставляются оценки.
Одним из направлений практико-ориентированного обучения математическому анализу в педвузе является работа с тестами.
IV. Организация работы с тестами
В вузах сегодня широко используется блочно-модульная система обучения, поэтому каждый модуль дисциплины «Математический анализ» заканчивается компьютерным тестированием. На первом этапе изучения дисциплины мы предлагаем первокурсникам тестовые задания четырех типов.
I тип. Задания, которые направлены на понимание изученных определений, терминов, утверждений, а также на усвоение математической символики. Приведем примеры.
1. Установить, является ли последовательность монотонной, и указать, какой именно (возрастающей или убывающей) 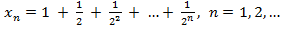 .
.
2. Установить, какие из приведенных последовательностей являются ограниченными (ответ обосновать):
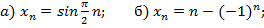
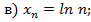
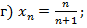
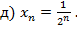
3. Установить истинность или ложность утверждения: «Всякая неограниченная снизу последовательность является отрицательной бесконечно большой».
4. Установить истинность или ложность утверждения: «Если функция непрерывна в данной точке, то она и дифференцируема в этой точке».
5. Установить истинность или ложность утверждения: «Если в данной точке существуют левая и правая производные функции 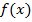 , то в этой точке существует и производная
, то в этой точке существует и производная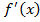 ».
».
Задания такого типа можно использовать на практических занятиях по математическому анализу в качестве контрольных вопросов. В этом случае студенты дают устные ответы с обоснованием или приведением контрпримеров. Такая работа направлена на формирование грамотной математической речи и умения корректно и лаконично выражать свои мысли, что важно для будущего педагога.
II тип. Задания на приведение примеров математических объектов по заданным условиям, типа «Приведите примеры»:
1) ограниченной и расходящейся числовой последовательности;
2) возрастающей и сходящейся к числу 3 числовой последовательности;
3) непрерывной, но не дифференцируемой в точке функции.
III тип. Задания, требующие использования математической символики. Например, записать символически:
1) определение бесконечно малой последовательности, привести пример;
2) определение расходящейся последовательности, привести пример.
IV тип. Задания на использование геометрических представлений (изображений) и геометрических интерпретаций изученных понятий и утверждений. Они делятся на два типа: в одних требуется перевести определение понятия или содержание теоремы на геометрический язык, то есть раскрыть их геометрический смысл; в других – распознать понятие по его геометрическому образу, задать формулой изображенный геометрический объект или установить справедливость утверждения по данному графическому изображению.
Умения переводить информацию с естественного и аналитического языков на геометрический язык и обратно особенно важны для учителя математики, так как аналогичные задания ежегодно бывают представлены в материалах ЕГЭ.
Заключение
Мы указали лишь некоторые направления практико-ориентированного обучения математическому анализу студентов педагогического вуза, обозначив их как основные, отвечающие его специфике и предназначению. Можно выделить и другие направления, такие как обучение поиску решения задач, обучение доказательству, организация проектной деятельности и т.д. Однако эти направления реализуются не только при изучении математического анализа, но и при изучении других математических дисциплин.
Успешная реализация практико-ориентированного обучения возможна лишь при активной самостоятельной работе обучающихся, доля которой по математическим дисциплинам в учебных планах педвуза, согласно ФГОС ВО, значительно возросла. Для эффективной организации самостоятельной работы студентов по математическому анализу нами подготовлено и опубликовано учебное пособие, ориентированное не только на усвоение теоретического материала и методов решения задач, но и на формирование современного методического мышления будущих учителей математики.
Исследование выполнено в рамках внутривузовского гранта Мордовского государственного педагогического института им. М.Е. Евсевьева по теме «Разработка научно- и учебно-методического обеспечения дисциплины "Математический анализ" в условиях бакалавриата по направлению подготовки "Педагогическое образование"».



