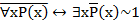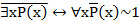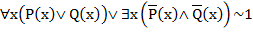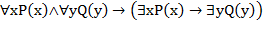В современных трудах исследователей в области образования значительное внимание уделяется разработке концепции гуманитаризации образования и определению особенностей компонентов методической системы, реализующей эту концепцию в учебном процессе. Реализация концепции гуманитаризации образования предполагает создание образовательной программы, нацеленной главным образом на повышение духовной культуры обучающихся, расширение кругозора, овладение методами научного поиска. Достижению этих целей способствует внесение в содержание обучения дополнительного материала, раскрывающего гуманистический аспект изучаемого предмета [1], отражение в методах обучения деятельностной природы знания [2].
Гуманистический аспект изучаемого предмета может раскрываться с помощью гуманитарного потенциала математики, в частности заданий, связывающих изучаемый материал с жизненным опытом и интересами обучающихся. Так, в профессиональной подготовке в вузе будущих учителей математики актуальна ориентированность математических дисциплин на школьный курс математики и методику его изучения, что способствует поддержанию положительной мотивации изучения математики студентами, а в дальнейшем – системному использованию этих знаний в изучении теории и методики обучения математике, на педагогической практике, в профессиональной деятельности [1].
Отражение в методах обучения деятельностной природы знания предполагает выделение состава учебной деятельности, адекватной познавательной деятельности в рамках осваиваемой предметной области. В частности, в учебном процессе в педвузе по математическим дисциплинам целесообразно практиковать методику работы над компонентами математического знания, учитывающую специфику поисковой математической деятельности [2].
Гуманитаризацию и гуманизацию математического образования связывают с такими направлениями реализации концепции фундаментализации математического образования, как универсализация математических знаний, умений и навыков, формирование общекультурных основ в процессе обучения. Под гуманизацией образования понимают такую организацию учебного процесса, при которой знания приобретают для обучающегося личностный смысл [2]. Гуманитаризацию образования рассматривают, как правило, анализируя концепцию гуманизации образования в содержательном аспекте. Так, основными положениями гуманитаризации математического образования называют направленность содержания обучения математике на всестороннее развитие личности обучающегося, выявление и применение в учебном процессе гуманитарного потенциала математики [1, 3].
Гуманитарный потенциал общего математического образования в свою очередь видят в формировании у обучающихся представлений об основных понятиях, аппарате математики, связях с другими науками и практикой, математических методах познания действительности, специфике поисковой математической деятельности, истории математики как части общечеловеческой культуры, а также в развитии культуры мышления, формировании математической культуры, научной картины мира, эстетическом воспитании обучающихся [4, 5].
Таким образом, можно сделать вывод о том, что реализация концепции гуманитаризации математического образования включает методическую разработку содержания математической предметной области, которое составляет гуманитарный потенциал математики, конструирование на основе этого содержания средств обучения математике. К средствам обучения, реализующим гуманитарный потенциал математики в математическом образовании, можно отнести следующие:
- учебный материал, раскрывающий структуру изучаемого содержания и логические связи в этом содержании;
- прикладные задачи, решение которых содействует раскрытию значимости приложений и практического применения учебного математического материала;
- учебный материал, демонстрирующий значимую роль математических методов в других областях знания;
- учебный материал, ориентированный на осваиваемую профессиональную деятельность;
- учебный материал занимательного характера;
- учебный материал, с помощью которого можно имитировать поисковую математическую деятельность;
- учебный материал, показывающий эстетику математических знаний;
- учебный материал, формирующий представление об истории математики и ее связях с историей человечества.
В статье рассматривается вопрос о конструировании средств обучения математической логике, реализующих гуманитарный потенциал математики в профессиональной подготовке в вузе студентов, обучающихся по направлению «Педагогическое образование».
Материалы и методы исследования. В учебной работе, учитывающей положения гуманитаризации математического образования, по курсу математической логики со студентами – будущими учителями математики целесообразно применять сюжетные задачи. Эти задачи и их решения имеют практический и занимательный характер, позволяют студентам лучше понять содержание основных понятий и аппарата математической логики, показывают возможность методической адаптации понятий и аппарата математической логики для школьников, то есть их можно отнести к средствам обучения, реализующим гуманитарный потенциал математики.
В статье перечислены виды сюжетных задач по курсу математической логики, приведены примеры таких задач, а также описаны ключевые моменты методики работы над этими задачами, учитывающей особенности обучения математическим методам познания действительности, в частности методу математического моделирования, а также особенности работы над компонентами математического содержания согласно деятельностному подходу в обучении. Изучение этих методических вопросов традиционно входит в курс теории и методики обучения математике, читаемый в вузе студентам, обучающимся по направлению «Педагогическое образование» с математическим профилем. Изложенные в статье задачи и методика работы над ними апробированы в учебном процессе по курсу математической логики со студентами Калужского государственного университета им. К.Э. Циолковского, обучающимися по направлению «Педагогическое образование», профиль «Физика и математика».
Результаты исследования и их обсуждение. Далее перечислим виды сюжетных задач по математической логике с примерами и методическими рекомендациями по их применению в учебном процессе.
1. Задачи на подведение под понятие «логическая причинно-следственная связь».
Пример такой задачи. Определите, есть ли логическая причинно-следственная связь между условиями «я умею», «я учился».
Решение. Событие «я умею и не учился» можно считать невыполнимым, поэтому логическая причинно-следственная связь между этими условиями есть, причем условие «я умею» является логической причиной, «я учился» – логическим следствием.
Методические рекомендации. При изучении логических связок «или», «следование», «равносильность» необходимо обратить внимание студентов на такую качественную особенность этих определений, как определение содержания логической связки через указание выполнимых и невыполнимых событий. Причем каждое такое событие описывается с помощью простых событий и логических связок «не», «и».
2. Задачи на выведение следствий из понятия «логическая причинно-следственная связь».
Пример такой задачи. Проанализируйте предложение с логической причинно-следственной связью «Если Вам это надо, то и нам это надо».
Решение. По формулировке предложения условие «Вам это надо» является логической причиной, а условие «Нам это надо» – логическим следствием. По определению логической связки «следование» невыполнимым является событие «Вам это надо и нам это не надо».
Методические рекомендации. При изучении логических связок «следование», «равносильность» следует рассказать студентам о типичных в математических текстах формулировках предложений с этими логическими связками. Так, предложение «Из А следует В» можно сформулировать «Если А, то В», «Для А необходимо В», «Для В достаточно А», «Все элементы со свойством А обладают свойством В». Предложение «А равносильно В» можно сформулировать «А тогда и только тогда, когда В», «Для А необходимо и достаточно В».
3. Задачи на применение понятий непротиворечивости, логического вывода, равносильности рассуждений.
Среди задач данного вида можно выделить следующие подвиды.
3.1. Сюжетные задачи на логический вывод.
Пример такой задачи. Если хлеб вкусный, то он свежий. Если хлеб не свежий, то он полезен для пищеварения. Если хлеб не вкусный, то он не полезен для пищеварения. Обязательно ли тогда весь хлеб свежий?
Решение. Целесообразно рассмотреть три способа решения сюжетной задачи на логический вывод.
1-й способ (анализ, способ решения, адаптированный для школьников).
По условию задачи можно выделить три свойства хлеба: вкусный, свежий, полезный для пищеварения. Перечислим все комбинации этих свойств, таких комбинаций 8.
1) Вкусный и свежий и полезный.
2) Вкусный и свежий и не полезный.
3) Вкусный и не свежий и полезный.
4) Вкусный и не свежий и не полезный.
5) Не вкусный и свежий и полезный.
6) Не вкусный и свежий и не полезный.
7) Не вкусный и не свежий и полезный.
8) Не вкусный и не свежий и не полезный.
Далее согласно условиям задачи исключаем невыполнимые комбинации. По условию «Если хлеб вкусный, то он свежий» невыполнимой является комбинация «Вкусный и не свежий», то есть 3 и 4. По условию «Если хлеб не свежий, то он полезен для пищеварения» невыполнимой является комбинация «Не свежий и не полезен для пищеварения», то есть 4 и 8. По условию «Если хлеб не вкусный, то он не полезен для пищеварения» невыполнимой является комбинация «Не вкусный и полезен», то есть 5 и 7.
Остались выполнимые комбинации 1, 2 и 6. На всех этих комбинациях условие «Хлеб свежий» выполняется. Значит, обязательно.
2-й способ (синтез, решение с помощью таблицы истинности).
Введем обозначения: А=«вкусный», В=«свежий», С=«полезный».
По условиям задачи составляем формулу математической логики:
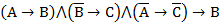
С помощью таблицы истинности убеждаемся, что она является тавтологией.
3-й способ (дедуктивный, решение с помощью правил логического вывода). Изложим формальное доказательство.
Учитывая 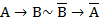 , получаем:
, получаем:
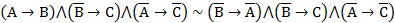 .
.
Поскольку 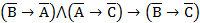 , то
, то
 .
.
Осталось сделать вывод: 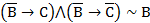 .
.
Методические рекомендации. При изучении понятия «логический вывод» сначала со студентами следует рассмотреть 1-й способ решения сюжетной логической задачи. Это решение помогает понять содержание этого понятия на качественном уровне: логический вывод справедлив тогда и только тогда, когда заключение верно на всех выполнимых по условию случаях.
Затем предложить студентам способ решения с помощью таблицы истинности, мотивируя необходимость владения этим способом решения тем, что при более сложно логически составленных условиях трудно выделить невыполнимые комбинации.
После этого в качестве примера рассмотреть для данной задачи применение дедуктивного способа решения. По ходу этого решения выписать все применяемые в нем правила логического вывода и все применяемые в нем равносильности. Затем предложить студентам доказать их справедливость (в подвиде 3.2. примеры 1–4).
3.2. Задачи на доказательство правил логического вывода, законов логики.
Студентам для доказательства следует предложить законы логики и правила логического вывода, которые нередко используются на практике, в частности в дедуктивных рассуждениях.
Например:
1) 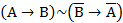 ;
;
2) 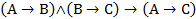 ;
;
3) 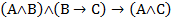 ;
;
4) 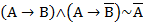 ;
;
5) 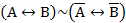
6) 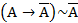 ;
;
7) 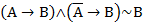 ;
;
8) 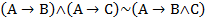 ;
;
9) 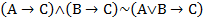 ;
;
10) 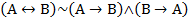 ;
;
11) 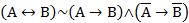 ;
;
12)  ;
;
13) 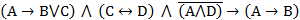 .
.
Методические рекомендации. Предложить студентам доказать правила логического вывода и законы логики как способом анализа, так и способом синтеза.
К изучению законов логики, сформулированных без кванторов, можно присоединить изучение законов логики, сформулированных с кванторами, и способов их доказательства. При этом понятие квантора ввести на этапе изучения формального языка математической логики.
Примеры задач на проверку справедливости правил логического вывода и доказательство законов логики, сформулированных с кванторами: с помощью аксиом математической логики проверьте справедливость предложений.
|
Аксиомы 1) 2) 3) |
Предложения 1) 2) 3) 4) 5) 6) 7) |
Решение
1) и 2) Пусть 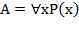 , то
, то 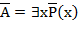 . Справедливы формулы
. Справедливы формулы 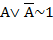 и
и 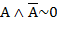 (закон исключенного третьего). Значит, справедливы формулы
(закон исключенного третьего). Значит, справедливы формулы 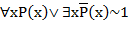 и
и 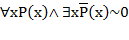 .
.
3) Преобразуем левую часть формулы 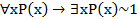 .
.
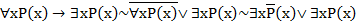
4) Возьмем отрицание от обеих частей формулы 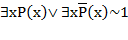 и получим формулу
и получим формулу  .
.
5) Формула 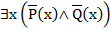 есть отрицание формулы
есть отрицание формулы 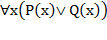 . Поэтому согласно закону
. Поэтому согласно закону 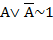 равносильность верна.
равносильность верна.
6) Рассмотрим случай, в котором формула принимает значение 0. Это случай 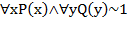 и
и 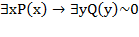 . Это условие равносильно условию:
. Это условие равносильно условию: 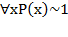 и
и 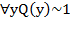 и
и 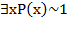 и
и 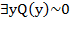 , что равносильно условию
, что равносильно условию 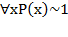 и
и 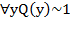 и
и 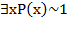 и
и 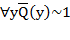 . Условия противоречивы. Значит, формула не принимает значение 0. Поэтому логический вывод верен.
. Условия противоречивы. Значит, формула не принимает значение 0. Поэтому логический вывод верен.
7) Введем обозначения 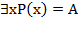 ,
, 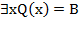 . Получим формулу
. Получим формулу 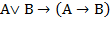 . Составим для нее таблицу истинности (табл. 1).
. Составим для нее таблицу истинности (табл. 1).
Таблица 1
Таблица истинности
|
|
|
|
|
|
|
1 |
1 |
1 |
1 |
1 |
|
1 |
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
1 |
1 |
|
0 |
0 |
0 |
1 |
1 |
Рассмотрим случай 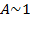 и
и 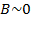 . Учитывая обозначения, это случай
. Учитывая обозначения, это случай 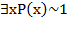 и
и 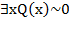 . Равносильный случай
. Равносильный случай 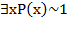 и
и 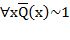 – выполнимый. Поэтому ноль во второй строке таблицы исключить не удается. Значит, логический вывод неверен.
– выполнимый. Поэтому ноль во второй строке таблицы исключить не удается. Значит, логический вывод неверен.
Методические рекомендации. Задачи на проверку справедливости логического вывода, доказательство законов логики, сформулированных с кванторами, можно предложить после усвоения правил логического вывода и законов логики, сформулированных без кванторов, поскольку решение этих задач опирается на знание этих правил и законов, а также знание способов доказательства их справедливости. В решении последних задач также используется понятие непротиворечивости условий на качественном уровне: условия непротиворечивы тогда и только тогда, когда они выполняются вместе.
3.3. Задачи на переформулирование предложений с помощью законов логики.
Пример такой задачи. С помощью закона логики 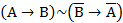 сформулируйте предложение, равносильное предложению «Если сомневаешься, то не делай».
сформулируйте предложение, равносильное предложению «Если сомневаешься, то не делай».
Ответ: «Если делаешь, то не сомневайся».
Пример такой задачи. С помощью закона логики
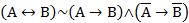 сформулируйте рассуждение, утверждающее равносильность условий «Умеешь», «Получится».
сформулируйте рассуждение, утверждающее равносильность условий «Умеешь», «Получится».
Ответ: «Если умеешь, то получится. Если не умеешь, то не получится».
3.4. Задачи на построение отрицаний предложений.
Примеры таких задач: сформулируйте отрицание предложений.
1) 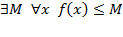 (определение ограниченной сверху функции).
(определение ограниченной сверху функции).
2) 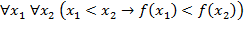 (определение возрастающей функции на ее промежутке непрерывности).
(определение возрастающей функции на ее промежутке непрерывности).
3) 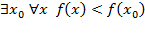 (определение точки, в которой функция принимает наибольшее значение).
(определение точки, в которой функция принимает наибольшее значение).
4) 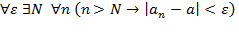 (определение предела последовательности).
(определение предела последовательности).
5) Каждый учитель любит всех своих учеников.
6) Каждый ключ открывает какую-нибудь дверь.
7) Есть задача, которую не может решить ни один студент.
8) Есть игра, которую любят все дети.
Методические рекомендации. С помощью этих задач вырабатывается умение применять законы математической логики в решении задач из других математических областей, практических задач.
3.5. Сюжетные задачи на проверку непротиворечивости рассуждения.
Пример такой задачи. Противоречивы ли условия «Ни один бармаглот не является хрюмзиком. Не все хрюмзики являются бармаглотами».
Решение. Предложение «Ни один бармаглот не является хрюмзиком» имеет синоним «Все бармаглоты не являются хрюмзиками», то есть содержит логическую причинно-следственную связь. Согласно определению логического следования невыполнимым является случай «Бармаглот и хрюмзик», то есть «Существует хрюмзик, который является бармаглотом».
Переформулируем предложение «Не все хрюмзики являются бармаглотами» с помощью законов математической логики и получаем предложение «Существует хрюмзик, который не является бармаглотом».
Исключенный и утверждаемый случаи не совпадают, значит, условия непротиворечивы.
3.6. Сюжетные задачи на анализ рассуждений.
Пример такой задачи. Проанализируйте рассуждение с помощью аппарата математической логики «Каждый квадрат является прямоугольником, но не каждый прямоугольник – квадрат».
Способ решения аналогичен способу решения предыдущей задачи.
4. Практические логические задачи.
Пример такой задачи. Для доказательства логического вывода проверили, выполняются ли причина и следствие вместе. Получили, что выполняются, и посчитали, что логический вывод доказан. Правильно ли поступили?
Решение. Сводится к проверке справедливости логического вывода 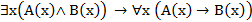 . Вывод неверен. Значит, поступили неправильно.
. Вывод неверен. Значит, поступили неправильно.
Неправильность логического вывода можно доказать следующим примером. Рассмотрим интерпретацию: 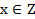 ,
,  = «
= «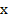 делится на 2»,
делится на 2», 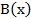 = «
= «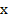 делится на 4».
делится на 4».
Пример такой задачи. С помощью математической логики осуществите дедуктивный переход от доказанного утверждения к целевому утверждению (табл. 2).
Таблица 2
Наглядный материал для сравнения доказанного и целевого утверждений
|
№ |
Доказанное утверждение |
Целевое утверждение |
|
1. |
Если функция возрастает (убывает) на промежутке, то ее производная неотрицательна (неположительна) на данном промежутке |
Если функция возрастает (убывает) на промежутке, то ее производная положительна (отрицательна) на этом промежутке |
|
2. |
Если производная положительна (отрицательна) на промежутке, то функция не убывает (не возрастает) на промежутке |
Если производная положительна (отрицательна) на промежутке, то функция возрастает (убывает) на этом промежутке |
Решение. В доказательстве используем утверждение «Производная функции равна нулю тогда и только тогда, когда эта функция есть константа» и правило логического вывода 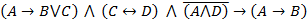 .
.
Методические рекомендации. Трудность в решении задач 3.5, 3.6, 4 состоит в составлении математической модели (структурирование рассуждения, составление формулы математической логики) рассуждения или практической ситуации, заключающей в себе логическую проблему.
Описанные в статье виды задач и последовательность изучения материала, соответствующая порядку следования представленных задач, апробированы в учебном процессе по курсу математической логики со студентами, обучающимися в вузе по направлению «Педагогическое образование» с математическим профилем. Студенты проявили к этим задачам интерес, отметили их занимательный характер, получили представление о значении математической логики для математики в целом, о возможности применения аппарата математической логики для разрешения логических проблем практического содержания, о возможности изучения элементов математической логики со школьниками и целях этой работы. Учебная работа с помощью представленных задач была направлена главным образом на усвоение основных понятий математической логики и способов применения ее аппарата для решения практических задач, чтобы в дальнейшем изучении математики, в профессиональной деятельности, в повседневной жизни студенты могли свободно опираться на имеющиеся знания, умения и навыки по математической логике. Возможность такой направленности учебной работы обеспечивается особенностями содержания, лежащего в основе составленных сюжетных задач по математической логике, а именно его гуманитарным характером.
Выводы. Комплекс тренировочных задач по математической логике, описанный в статье, представляет собой методическую разработку по курсу «Математическая логика» для студентов вузов, обучающихся по направлению «Педагогическое образование» с математическим профилем. Данный учебный материал составлен в соответствии с основными положениями концепции гуманитаризации педагогического математического образования и может применяться в учебном процессе по курсу математической логики для студентов вузов – будущих учителей математики и содействовать более глубокому усвоению математического содержания и обобщенных способов действия, необходимых учителю математики для успешного осуществления профессиональной деятельности.
Материалы, которые можно использовать в учебном процессе по математике, при изучении элементов математической логики со студентами вузов гуманитарных направлений подготовки, изложены в статье [6]. Для учебно-методического обеспечения курсов «Математика» и «Математическая логика» для студентов педагогических направлений подготовки, в частности с математическим профилем, для студентов гуманитарных направлений подготовки разработано учебно-методическое пособие [7], которое ориентировано на применение гуманитарного потенциала математической логики в учебном процессе по математике в вузе.