Если попытаться проанализировать основные тенденции развития современной науки, к которым, несомненно, можно отнести такие, как междисциплинарность, дифференциацию и интеграцию научных знаний, их всемерную математизацию и компьютеризацию, значительное ускорение роста научного знания, возрастание роли методологии в структуре научного знания, рост сегмента прикладной составляющей науки, то следует подчеркнуть роль методологии как рядоположенного в указанном перечне, так и методологическое влияние на все остальные отмеченные тенденции. Рассматривая методологию как совокупность познавательных средств (в самом широком смысле этого слова), необходимо отметить, что в системе методов научного познания, характерных для общенаучной методологии, моделирование можно позиционировать как один из ведущих и наиболее востребованных в современной науке. Принимая известный тезис «образование – модель науки», можно сделать вывод о значимости указанного метода в образовании в целом, и в физике как учебной дисциплине в частности, ибо физика является одной из ведущих учебных дисциплин в формировании методологического фундамента современного школьного образования.
Традиционно моделирование сводится к воспроизведению определенных свойств (характеристик) объекта на ином, специально созданном объекте, который и принято называть моделью [1]. В этом процессе субъект, выполняющий указанные действия, ориентируется на существенные, знаковые, ключевые характеристики (свойства) рассматриваемого объекта с учетом и на основе определенного контекста, ибо в иных условиях, при достаточной методологической подготовке субъекта, будут вычленяться иные ключевые свойства. Ориентир на воспроизведение в модели ключевых характеристик объекта (с учетом контекста) и является основой процесса моделирования, что непосредственно связано с использованием семиотических механизмов в познавательном процессе.
Не останавливаясь на анализе и характеристике семиотики как науки, отметим лишь основные функции знаковых систем, к которым следует отнести передачу информации, выражение смысла, а также механизмы общения (простейшие системы сигнализации, естественные языки, формализованные языки науки) [2]. Реализация каждой из отмеченных функций предполагает целенаправленную работу по вычленению знаков, механизмов их сочетания, а также организацию знаковой системы на основе определенного системообразующего фактора, сопряженного с контекстом.
Каждая формируемая модель представляет собой некую абстракцию, ибо в процессе моделирования субъектом акцентируется внимание, прежде всего, на существенных свойствах объекта, абстрагируясь от несущественных для данного случая. Тем самым для исследования используется ограниченный набор характеристик объекта, что может существенно повысить эффективность познавательного процесса. Однако такое сокращение списка рассматриваемых характеристик объекта может привести исследование к некорректному результату, ибо в процессе «сокращения» может быть по ряду причин отброшена какая-либо существенная характеристика объекта. Целенаправленное обучение основам моделирования, связанным с отбором ключевых, знаковых характеристик объекта для последующего исследования (без изменения свойств целостного объекта), является одной из важнейших задач современного образовательного процесса в контексте средней и высшей школ, ибо отбор и систематизация предлагаемой информации следует считать одной из важнейших проблем, стоящих перед современным человеком вне зависимости от его возраста, уровня образования и сферы деятельности.
Основные этапы, механизмы построения модели в значительной степени схожи с основными этапами, алгоритмом абстрагирования, что, несомненно, позволяет говорить о взаимодополнительности мыслительной операции (МО) абстрагирования и метода научного познания [3]. Проиллюстрируем этот тезис кратким примером из курса физики средней школы. Аналогичные примеры, их содержательные формы позволяют практикующим педагогам активно внедрять методологический компонент в школьное физическое образование. В процессе целенаправленной работы по формированию мыслительной операции «абстрагирование» можно воспользоваться объектами с пошаговым упрощением (или усложнением) их структуры и содержания (рис. 1).
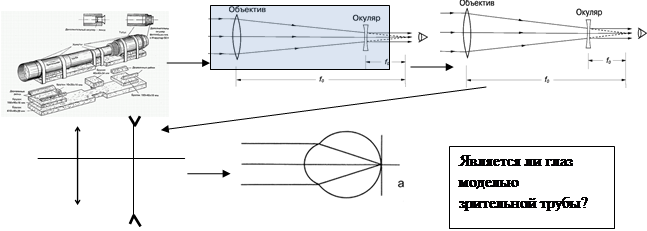
Рис. 1. Этапы абстрагирования физического объекта
Несколько изменив содержание приведенной последовательности, можно и по-иному сформулировать вопрос – «Является ли зрительная труба моделью глаза?». В данном случае в результате абстрагирования мы получили некую модель реального объекта, в данном случае зрительной трубы. Необходимо отметить, что «узнаваемость» моделируемого объекта сохранилась, однако отдельные специфические особенности в процессе абстрагирования утеряны. В данном случае в соответствии с задачей была построена абстрактная модель зрительной трубы. Последующие действия, связанные с условным упрощением, могли бы привести к лишению полученной модели специфики исходного объекта.
Модели, применяемые в образовательном процессе, являясь своеобразным отображением моделей, сформированных в условиях базовой науки, выступают в качестве необходимого и во многом определяющего звена в усвоении методологических знаний, что является основой для освоения содержания образования. Моделирование как метод научного познания, процесс построения модели представлено в конкретных школьных учебных дисциплинах (и в физике в том числе) в явно усеченном виде, с использованием лишь отдельных элементов многомерного процесса моделирования и не носит целенаправленный характер. К таким видам деятельности можно отнести составление плана параграфа учебника или какого-либо произведения, построение графиков (без акцентов на процессе), применение содержательных форм заданий типа: «Чем мы можем заменить… ?», «Предложите способ…» и некоторые другие (список весьма ограничен).
Всемерное акцентирование внимания обучаемых на ключевых, знаковых для данных условий особенностях процесса моделирования или анализа построенной модели оказывает положительное влияние на обучение основам моделирования как одной из важнейших структурных составляющих механизма познавательного процесса [4; 5].
Рассмотрим пример, иллюстрирующий основные элементы семиотического подхода при создании геометрической модели технического устройства, известного как уголковый отражатель, часто используемый школьными учителями физики при изучении оптических явлений, который может быть использован для построения аналогичных моделей в иных разделах.
Прежде всего, охарактеризуем понятия «геометрическое моделирование», «геометрическая модель». Геометрическое моделирование является дисциплиной, представляющей методы, решения задач, имеющих геометрическую сущность, с использованием геометрических моделей различной размерности [6]. С этой точки зрения моделирование трехмерного пространства с использованием эпюра Монжа (чертежа) является простейшим случаем использования идей и методов геометрического моделирования. В рамках школьного образования начальные сведения о геометрическом моделировании учащиеся получают на уроках черчения и геометрии [7]. Черчение как учебный предмет не входит в базовый учебный план, однако в вариативную часть весьма часто включается и является востребованным, что убедительно подтверждается массовостью и содержанием регулярно проводимой Санкт-Петербургской городской олимпиады по черчению. Несмотря на необычность и сложность рассматриваемых материалов, школьники весьма успешно их осваивают: в школах и гимназиях - в рамках спецкурсов, а в естественно-научном лицее при Санкт-Петербургском политехническом университете Петра Великого - на уроках.
Формирование образа исследуемого объекта происходит на основе имеющихся у учащихся сведений о моделируемом объекте и физических принципах его действия.
Действие уголкового отражателя основано на законах геометрической оптики, т.е. физические процессы полностью описываются геометрическими характеристиками, имеющими визуальные образы, и соответственно действие уголкового отражателя можно представить некоторой геометрической моделью. Создаваемая геометрическая модель предполагает, что уголковый отражатель представляет собой четырехгранную пирамиду, произвольным образом располагающуюся в пространстве и имеющую три взаимно перпендикулярные зеркальные грани AOB, BOC, АOС (рис. 2).
Проекционная геометрическая модель уголкового отражателя создается с использованием метода преобразования проекционной картины, известного как метод дополнительного ортогонального проецирования. Геометрические построения, используемые в этом методе, кажутся несколько громоздкими, но они основаны на знаниях и умениях учащихся, получаемых, в частности, в курсе черчения.
Создаваемая нами геометрическая модель реализует три этапа решения задачи.
1. Создание графического образа уголкового отражателя как некоторой жесткой системы трех взаимно перпендикулярных плоскостей, имеющей возможность управления ее пространственным положением. Формирование графического образа падающего луча, предполагающего возможность управления его пространственным положением.
2. Определение условий падения и отражения светового луча на соответствующих гранях уголкового отражателя и как итог – определение траектории отраженного луча.
3. Построение в исходной геометрической модели траектории отраженного луча и при желании построение аксонометрического изображения, иллюстрирующего работоспособность созданной модели. В качестве критерия работоспособности принимаем условие параллельности падающего на уголковый отражатель и отраженного от него лучей.
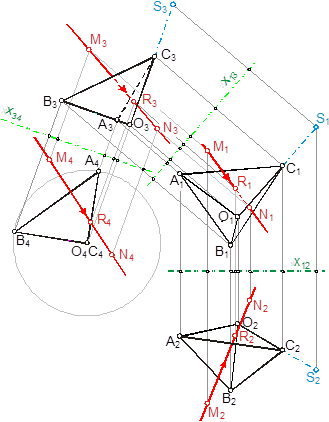
Рис. 2. Геометрическая модель уголкового отражателя, реализующая возможности управления его положением и траекторией падающего луча
Первый этап. Исходная геометрическая модель уголкового отражателя и падающего светового луча создается в полях проекций π1 - π2. Управление пространственным положением объекта осуществляется изменением положения ребра OS, являющегося основным конструктивным элементом, отвечающим за «жесткость» рассматриваемого объекта. Возможность вращения уголкового отражателя относительно ребра OS достигается введением дополнительных плоскостей проекций π3 – π4. Управление положением падающего луча MN достигается путем изменения положения проекций точек M, N на соответствующих линиях проекционной связи.
Второй этап. Дальнейшее решение задачи строится на использовании знаний учащихся, полученных в курсе геометрической оптики, а именно того факта, что падающий и отраженный лучи лежат в одной плоскости и значение угла падения равно значению угла отражения.
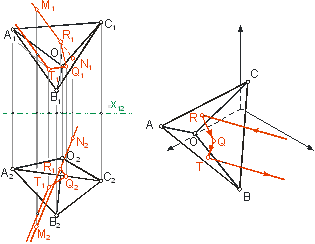
Так как перед нами стоит задача построения траектории луча внутри уголкового отражателя, нам необходимо трижды рассмотреть задачу об определении углов падения луча на соответствующие грани (рис. 3), преобразуя проекционную картину так, чтобы мы имели возможность наблюдать истинные значения углов падения и траекторию отраженных лучей.
Третий этап. В результате трехкратного отражения светового луча на гранях уголкового отражателя получаем траекторию отраженного луча, параллельную падающему лучу. Факт параллельности лучей рассматриваем как подтверждение того, что созданная геометрическая модель адекватна реальным физическим условиям (рис. 4), что находит свое отражение и на аксонометрической проекции, визуализирующей созданную геометрическую модель.
Разработанная геометрическая модель уголкового отражателя реализована с использованием системы геометрического моделирования «Симплекс» [8; 9]. Анализ полученных результатов показал, что созданная геометрическая модель адекватно реагирует на изменения пространственного положения уголкового отражателя и падающего светового луча.
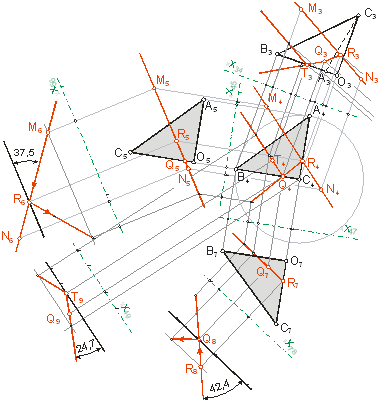
Рис. 3. Определение траектории луча в уголковом отражателе
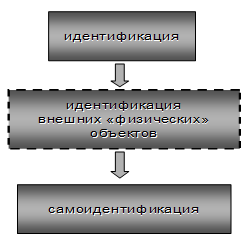
Представленный в статье подход и рассмотренные примеры соответствующих методических материалов позволяют сделать вывод о возможности реализации следующей логической цепочки семиотического характера (рис. 5).
|
|
|
|
Рис. 4. Результат работы геометрической модели уголкового отражателя |
Рис. 5. Логическая цепь семиотического характера |
На базе формируемого механизма идентификации физических объектов выстраиваются основы самоидентификации различного уровня и, как следствие, реализация логической последовательности семиотического характера «факт, знак, тест (рисунок), интерпретация, значение», которая также, несомненно, может быть использована в школьном образовательном процессе по физике применительно к моделированию.
Таким образом, формируемые с использованием геометрического моделирования семиотические механизмы на базе предметной области физики, в силу своей общности могут быть экстраполированы на иные учебные дисциплины с целью активизации методологического компонента познавательного процесса, что в конечном итоге будет активно способствовать реализации идей междисциплинарного взаимодействия, которые во многом являются основой современных образовательных стандартов и соответствуют стратегическим направлениям развития современной науки.