Особенность нового поколения основных профессиональных образовательных программ высшего образования (ОПОП ВО) заключается в реализации идей компетентностного подхода, являющегося основой Федеральных государственных образовательных стандартов Высшего образования (ФГОС ВО). При этом под компетентностным подходом понимается следующее:
- отражение в системном и целостном виде образа результата образования;
- формулирование результатов образования в вузе как признаков готовности выпускника продемонстрировать соответствующие знания, умения и ценности;
- определение структуры компетенций, которые должны быть приобретены и продемонстрированы обучаемыми.
Компетентностные модели бакалавров, закрепленные во ФГОС ВО, включают общекультурные, общепрофессиональные, профессиональные компетенции. Компетенция – это способность применять знания, умения, личностные качества и практический опыт для успешной деятельности в определенной области.
ФГОС ВО по направлению подготовки 44.03.01 «Педагогическое образование» определяет требования к результатам освоения программы бакалавриата через перечень общекультурных, общепрофессиональных и профессиональных компетенций. В Стандарте отмечено, что при разработке программы бакалавриата организация вправе дополнить набор компетенций выпускников с учетом направленности программы на конкретные области знания и (или) виды деятельности. Таким образом, ОПОП ВО дополняется специальными профессиональными компетенциями (СПК), учитывающими профиль подготовки и отражающими специфику конкретной предметной или надпредметной сферы профессиональной деятельности [4]. Определение СПК осуществляется на основе профессионального стандарта педагога, а также требований к должностям «Учитель», Единого квалификационного справочника должностей руководителей, специалистов и других служащих (ЕКС).
В связи с этим в системе высшего педагогического образования актуальны следующие проблемы:
1) определение специальных профессиональных компетенций с учетом профиля и специфики конкретной предметной (надпредметной) области;
2) поиск современных форм, методов и средств обучения, в условиях которых возможно эффективное формирование и оценка уровня сформированности указанных компетенций в процессе аудиторной и внеаудиторной самостоятельной работы обучающихся.
Цель и задачи исследования. Актуализация проблемы определения, формирования и оценки специальных профессиональных компетенций в компетентностной модели бакалавра по направлению «Педагогическое образование» привела к необходимости структурного анализа соответствующего профессионального стандарта, а также к исследованию и модернизации активных и интерактивных технологий обучения, реализующих в полной мере идеи компетентностного подхода. Нами были поставлены следующие задачи:
1) определить специальные профессиональные компетенции по направлению подготовки 44.03.01 «Педагогическое образование» для математического профиля;
2) определить и апробировать технологии обучения, позволяющие эффективно развивать и оценивать уровень сформированности специальных профессиональных компетенций в процессе аудиторной и внеаудиторной самостоятельной работы студентов.
Результаты исследования и их обсуждение. В Кемеровском государственном университете по направлению подготовки 44.03.01 «Педагогическое образование», профиль «Математика», были определены следующие специальные профессиональные компетенции:
- СПК-1: способен получать, демонстрировать, применять и критически оценивать знания в области математики;
- СПК-2: способен использовать знания и умения в области математики и ее обучения для решения профессиональных задач;
- СПК-3: способен понимать универсальный характер математических законов, прикладное, научное, общекультурное и историческое значение математики.
Указанные компетенции были сформулированы на основе трудовой функции из профессионального стандарта (ПС) 01.001 «Педагог (педагогическая деятельность в дошкольном, начальном общем, основном общем, среднем общем образовании) (воспитатель, учитель)» «Модуль "Предметное обучение Математика" В/04.6» [3]. При этом была установлена следующая взаимосвязь между трудовыми действиями из профессионального стандарта и СПК (таблица).
Взаимосвязь между трудовыми действиями (из ПС) и СПК
|
СПК (по ФГОС ВО) |
Трудовые действия из ПС |
|
СПК -1
|
- Формирование способности к постижению основ математических моделей реального объекта или процесса, готовности к применению моделирования для построения объектов и процессов, определения или предсказания их свойств. - Формирование внутренней (мысленной) модели математической ситуации (включая пространственный образ). - Формирование конкретных знаний, умений и навыков в области математики |
|
СПК-2 |
- Формирование у обучающихся умения проверять математическое доказательство, приводить опровергающий пример. - Формирование у обучающихся умения выделять подзадачи в задаче, перебирать возможные варианты объектов и действий. - Формирование у обучающихся умения пользоваться заданной математической моделью, в частности формулой, геометрической конфигурацией, алгоритмом, оценивать возможный результат моделирования (например - вычисления) |
|
СПК-3 |
- Формирование материальной и информационной образовательной среды, содействующей развитию математических способностей каждого ребенка и реализующей принципы современной педагогики. - Предоставление информации о дополнительном образовании, возможности углубленного изучения математики в других образовательных и иных организациях, в том числе с применением дистанционных образовательных технологий. - Формирование представлений обучающихся о полезности знаний математики вне зависимости от избранной профессии или специальности. - Формирование способности к логическому рассуждению и коммуникации, установки на использование этой способности, на ее ценность. - Развитие инициативы обучающихся по использованию математики |
Внедрение ФГОС ВО на основе компетентностного подхода актуализировало значимость применения активных и интерактивных форм и технологий в процессе обучения. Одной из таких технологий, применяемых нами при освоении обучающимися дисциплины «Геометрия» с целью формирования СПК-1 (способен получать, демонстрировать, применять и критически оценивать знания в области математики), является кейс-технология (технология анализа конкретных ситуаций). Суть ее заключается в том, что обучающимся предлагают осмыслить реальную жизненную ситуацию. В процессе ее разрешения студент актуализирует знания, полученные ранее, или включается в процесс поиска и последующего применения новых знаний. При этом учебная проблема может не иметь однозначных решений, что позволяет преподавателю варьировать ход занятия [1].
Примерная структура кейса включает введение (название кейса, постановка задачи), формулирование проблемы (описание проблемной ситуации), материалы для решения (могут быть структурированы в форме вопросов).
Приведем пример структуры кейса по разделу «Аналитическая геометрия на плоскости».
1. Кейс «Способы заданий и уравнения прямой на плоскости»
Задача: Актуализация и открытие знаний о прямой на плоскости.
2. Ситуация
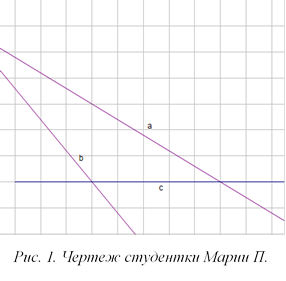
При выполнении курсового проекта студентке Марии П. требовалось провести прямую через точку пересечения двух данных прямых a и b под заданным углом α=45° к третьей прямой с. Однако в процессе выполнения работы случилась неприятность: точка пересечения прямых a и b оказалась за пределами чертежа (рис. 1). Перечерчивать заново студентке не хотелось: пришлось бы переделывать несколько страниц.
Проблема
Провести прямую через точку пересечения двух данных прямых, находящуюся за пределами чертежа, под углом 45° к заданной третьей прямой (формулируют обучающиеся).
3. Вопросы для работы с кейсом
- Можно ли решить задачу методом координат?
- Как выбрать систему координат наиболее удобным образом?
- Сформулируйте геометрический смысл углового коэффициента прямой.
- Как найти точку пересечения двух прямых, заданных своими уравнениями?
- Запишите уравнение прямой, заданной двумя точками.
- Запишите уравнение прямой, заданной точкой и угловым коэффициентом.
- Можно ли решить задачу, не используя метод координат?
- В чем вы видите преимущества и недостатки метода координат при решении данной задачи?
Кейс-технология является одним из эффективных средств оценивания уровня сформированности компетенций. Потребность в применении кейс-измерителей обусловлена тем, что оценка функциональных компетенций не может сводиться к ответам на вопросы тестового характера, поскольку функциональные компетенции – это то, что человек должен уметь делать в трудовой сфере или решении логических задач. Описание функциональных компетенций, как правило, предполагает формулировки деятельностного типа. Сформулированные нами специальные профессиональные компетенции являются функциональными компетенциями. Наиболее эффективным способом их оценивания является решение кейсов (реальных проблемных ситуаций), основанных на совокупности ситуационных моделей, включающих формулирование законов, определений, тенденций, прогнозов [1].
При оценке работы с кейсом можно использовать следующие критерии:
- была сформулирована и проанализирована проблема, заложенная в кейсе;
- были продемонстрированы адекватные аналитические методы при работе с информацией;
- были использованы дополнительные источники информации для решения кейса;
- были выполнены все необходимые расчеты,
- выводы обоснованны, аргументы весомы;
- сделаны собственные выводы, которые отличают данное решение кейса от других решений.
Достижение результатов освоения программы бакалавриата через овладение общекультурными, общепрофессиональными и специальными профессиональными компетенциями предполагает углубление, расширение знаний, умений; освоение инновационных методов обработки информации. Это требует создания определенных условий обучения, в которых студент сможет проявить познавательную, интеллектуальную активность, представить свою индивидуальность как субъекта учебного процесса.
Дисциплины математического и естественно-научного цикла нуждаются в высокой степени визуализации учебного материала, так как они имеют сложный понятийный аппарат, сложные объекты и системы с многоуровневой структурой, требующие глубокого анализа, т.е. разделения, сравнения, свёртывания, установления логических и смысловых связей, систематизации учебного материала. Одним из методов, способствующим решению перечисленных трудностей, является метод логико-смыслового моделирования информации, относящийся к технологии визуализации учебной информации [7]. Этот метод применяется нами при изучении курса «Теория вероятностей и математическая статистика». Логико-смысловые модели (ЛСМ), предложенные доктором педагогических наук В.Э. Штейнбергом, представляют собой координатно-матричный каркас опорно-узлового типа, на который наносится информация в виде ключевых слов (разделение темы на координаты); определяется расположение координат; выделяются узловые элементы содержания; выявляются смысловые связи между узловыми элементами; свертывается информация на узлах до ключевых слов (развёртывается в процессе речевой деятельности) [6].
Применение логико-смысловых моделей при изучении теории вероятностей и математической статистики способствует систематизации полученных знаний, установлению их связности, выделению ключевых элементов содержания предмета, выполнению различных действий по переработке и усвоению знаний: анализ и синтез получаемой информации, обобщение, сравнение и упорядоченное её расположение.
При проектировании логико-смысловых моделей мы придерживаемся одного и того же вида координатно-матричного каркаса: число координат остается равным восьми; отсчет узлов всегда начинается от центра; важнейшие смысловые связи между узлами наносятся в виде матриц связи.
Логико-смысловые модели учебного содержания разрабатываются как для целых разделов, так и для отдельных тем. Изучаемая тема представляет собой некоторое пространство знаний, которое необходимо структурировать, поэтому конструирование логико-смысловой модели для преподавателя и для студента включает следующие процедуры: выделение ключевой идеи, выбор темы или объекта изучения, которые помещаются в центр логико-смысловой модели; выделение тезисов идеи, определение набора координат (основных вопросов темы) путем расщепления на отдельные группы; ранжирование координат (определение плана или последовательности изучения); определение опорных узлов на каждой координатной оси, представляющих ключевые моменты изучаемой темы; ранжирование опорных узлов координатных осей согласно алгоритму изучения либо другому основанию; заполнение элементов матриц связи между опорными узлами.
Все обозначенные элементы (координаты, опорные узлы, узлы матриц связи) заполняются названиями, состоящими из минимального количества слов.
Разработанная логико-смысловая модель не является единственно правильной, а служит лишь вариантом представления изучаемой темы или раздела. Это учитывается при индивидуальной или групповой разработке ЛСМ в ходе выполнения самостоятельной работы.
При разработке логико-смысловой модели учебного содержания некоторых тем или разделов курса возможно видоизменять координатно-матричный каркас, располагая элементы учебного содержания на координатах не в строгой последовательности его изучения, а в зависимости от лучшего зрительного восприятия модели. Так, к примеру, выглядит логико-смысловая модель учебного содержания раздела «Случайные величины», где отсутствующие узлы связи предлагается воспроизвести студентам (рис. 2).
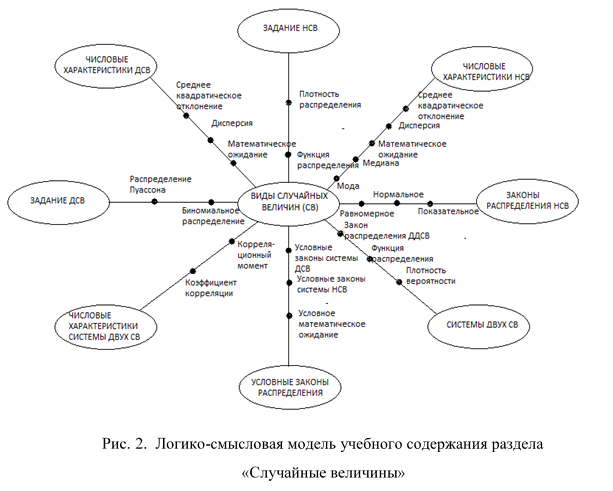
Опыт показывает, что целесообразно представлять студентам логико-смысловую модель только в виде координатного каркаса, а координатные узлы и матрицы связи между узлами координат (где это возможно) студенты могут заполнить самостоятельно, получив необходимую учебную информацию на лекционных занятиях либо при самостоятельном изучении материала. При этом работать студенты могут как индивидуально, так и микрогруппами. Самостоятельное выявление связей между опорными узлами координатных осей является наиболее важным условием для успешного обучения. Сконструированные самостоятельно логико-смысловые модели студенты могут использовать для подготовки к сдаче зачетов и экзаменов.
Использование логико-смысловых моделей помогает студентам в наглядной, свернутой форме воспринимать новый и воспроизводить уже изученный материал. Всё больший объем учебной информации требует от студентов увеличения скорости её обработки, которая, в свою очередь, зависит от наглядности, простоты изложения учебного материала, от ясности выражения его сути. Пояснение основных определений, терминов, свойств схемами, моделями или рисунками способствует качественному изучению и запоминанию новых знаний, возможности самостоятельного проведения контроля их усвоения. Самостоятельное конструирование логико-смысловых моделей позволяет студентам: воспринимать объекты изучения как целостные образы; анализировать информацию за счет каркасной формы модели; повышать эффективность учебной деятельности в процессе выполнения операций переработки и усвоения знаний (выделение узловых элементов, их ранжирование, систематизация, установление смысловых связей). Опыт по созданию многомерного дидактического инструментария в форме логико-смысловых моделей может существенно помочь будущим специалистам в их профессиональной деятельности.
Эффективное формирование специальных профессиональных компетенций (СПК) невозможно без овладения студентами навыками самостоятельного мышления, реализуемыми через грамотно организованную самостоятельную работу.
Обращаясь к проектированию внеаудиторной самостоятельной работы студентов (ВСРС) по дисциплинам предметной подготовки будущего учителя математики, мы пришли к выводу, что ВСРС целесообразно строить на интеграции таких методологических подходов как: компетентностный, системный, деятельностный и личностно ориентированный. При осуществлении такой интеграции мы руководствуемся следующими концептуальными принципами: модульная организация ВСРС; вариативность содержания и объема ВСРС; уровневая и элективная дифференциация ВСРС; профессионализация учебных заданий для ВСРС; контроль и оценка индивидуальных достижений студентов во ВСРС по предмету; информационно-методическое обеспечение ВСРС [5].
Модульная организация ВСРС обеспечивает систематичность и регулярность этого вида учебных занятий. Вариативность содержания и объема ВСР позволяют студенту дозировать ее с учетом требований образовательного стандарта, личностных особенностей, интересов и возможностей. Уровневая и элективная дифференциация учебных заданий обязательной и дополнительной частей ВСР дают студенту возможность конструировать индивидуальную траекторию учения в рамках каждого модуля дисциплины. Профессионализация учебных заданий ВСР путем их ориентации на формирование ряда методических умений, характерных для профессиональной деятельности учителя математики, способствует развитию учебной и профессиональной мотивации студентов. В комплексной оценке ВСР (на основе балльно-рейтинговой системы и портфеля индивидуальных достижений студента), осуществляемой обоими субъектами учебного процесса (преподавателем и студентом), интегрированы результаты всей самостоятельной учебно-познавательной деятельности студентов в течение семестра. Информационно-методическое обеспечение ВСРС включает учебно-методическую документацию по организации и планированию всех видов СРС.
Ориентиром проектирования всех компонентов методической системы ВСРС – будущих учителей математики мы выбрали ее системообразующий элемент, то есть цель: формирование СПК будущих учителей математики.
При этом проектирование осуществляется в пять этапов: модульное структурирование учебного содержания; разработка и обоснование структурной модели самостоятельной работы студентов по каждому модулю с учетом необходимости формирования компонентов СПК и специфики будущей профессиональной деятельности; составление учебных заданий для внеаудиторной самостоятельной работы студентов по каждому модулю; разработка технологии контроля и оценки внеаудиторной самостоятельной работы студентов на основе сочетания двух методик: балльно-рейтинговой оценки и портфеля индивидуальных достижений студента; разработка критериально-оценочного аппарата для установления уровней сформированности СПК.
Второй этап проектирования представляет особый интерес, так как он отражает специфику внеаудиторной самостоятельной работы студентов.
Обязательная часть ВСРС – это решение многокомпонентного задания, структурные элементы которого: решение индивидуальной работы, деятельностно-ценностной задачи и самостоятельное составление задач [2]. Выполнение такого задания обеспечивает формирование у студентов всех компонентов СПК.
Индивидуальная работа представляет набор ключевых задач модуля, решение которых требует знания и использования основных свойств изучаемых понятий.
Процесс конструирования задач благоприятно влияет на усвоение изучаемого материала, приучает студентов включать знания в реальную действительность, делать обобщения и выводы, точно формулировать свои мысли, использовать алгоритмы и схемы для решения задач.
Деятельностно-ценностные задачи помогают обеспечить целостность предметной подготовки будущего учителя, обогатить представления студентов сведениями об использовании полученных знаний в других областях человеческой деятельности, сформировать систему ценностей, как результат собственной учебной деятельности.
Выводы. На основании выполненных авторами исследований по проблемам определения, формирования и оценки специальных профессиональных компетенций в компетентностной модели бакалавра по направлению «Педагогическое образование» (профиль «Математика») были сделаны следующие выводы.
1. СПК целесообразно формулировать на основе трудовой функции из профессионального стандарта педагога, устанавливая взаимосвязи между трудовыми действиями из ПС и содержанием специальных профессиональных компетенций. Таким образом, были определены следующие специальные профессиональные компетенции: СПК-1: способен получать, демонстрировать, применять и критически оценивать знания в области математики; СПК-2: способен использовать знания и умения в области математики и ее обучения для решения профессиональных задач; СПК-3: способен понимать универсальный характер математических законов, прикладное, научное, общекультурное и историческое значение математики.
2. СПК формируются и оцениваются с помощью дисциплин предметной подготовки, в процессе обучения которым используются активные и интерактивные педагогические технологии. В частности, опытным путем установлена эффективность «кейс-технологии» и технологии визуализации учебной информации (метод логико-смысловых моделей).
3. Эффективное формирование СПК требует грамотного проектирования внеаудиторной самостоятельной работы студентов (ВСРС). Работу целесообразно строить на интеграции таких методологических подходов, как компетентностный, системный, деятельностный и личностно ориентированный, руководствуясь следующими концептуальными принципами: модульная организация ВСРС; вариативность содержания и объема ВСРС; уровневая и элективная дифференциация ВСРС; профессионализация учебных заданий для ВСРС; контроль и оценка индивидуальных достижений студентов во ВСРС по предмету; информационно-методическое обеспечение ВСРС.



