Проблемы российского высшего технического образования известны [1]:

• спад экономического развития в связи с кризисом существенно уменьшил интерес к обучению по техническим направлениям и специальностям (кроме связанных с нефтью и газом);
• введение ЕГЭ при отсутствии обязательного экзамена по физике;
• создание профильных школ не способствовало изучению физики в школе;
• подготовка к ЕГЭ в школе, а также с репетитором существенно уменьшает способность школьников к самостоятельной работе.

Кроме того, под влиянием информационного бума, сопровождаемого большим объемом информации, все более усугубляется тенденция: в ограниченное время обучения изложить все больше разноплановых сведений, не связанных между собой жесткой логической связью. Принципиально противостоять этому подходу может только перенос акцентов на структурно-функциональный метод познания, позволяющий осмыслить и усвоить незыблемый, только постепенно и логически наращиваемый каркас фундаментальных знаний, фиксирующий и укрепляющий предметные и особенно межпредметные связи [2].

В связи с этим среди многих проблем современного естественно-научного образования проблема согласования курсов физики и математики стоит весьма остро. Вообще говоря, идеальное согласование названных курсов настолько трудоемко, что считается невозможным, потому что уже на первых лекциях по физике студенту необходимо знать элементы векторной алгебры, дифференциального и интегрального исчислений, понятие градиента скалярной величины и т.д. [4].

В некоторых зарубежных вузах эта проблема решается следующим образом: на первом курсе (пока читаются необходимые для изучения курса физики разделы математики) в курсе физики повторяется школьная программа.

Авторы первым этапом согласования предлагают изучение учебного плана направления или специальности. Затем, после изучения программного материала физики и математики, необходимо выявить темы для согласования, разработать целевые установки для трехуровневого контроля знаний студентов по выделенным темам. Следующий этап – это составление задания к курсу физики на основе межпредметных связей. Преподаватели разрабатывают методическое обеспечение для выполнения заданий к курсу физики.

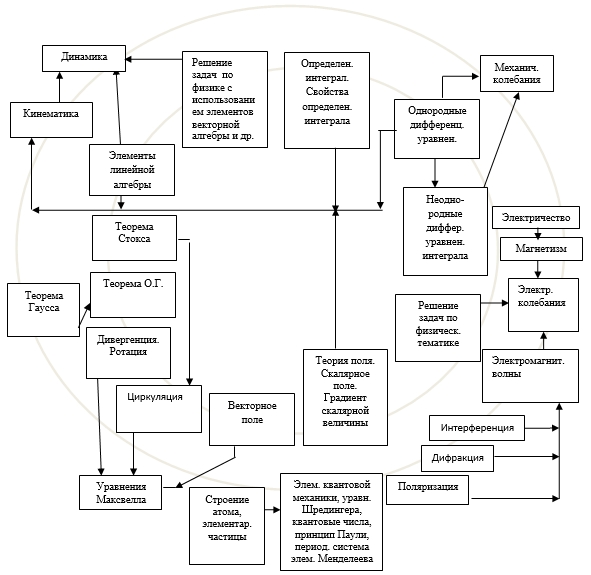
Согласование курсов физики и математики по последовательности изложения и тематике материала

На основе согласования в рабочие программы внесены необходимые изменения. Составленные на основе учета межпредметных связей программы дисциплин и каталог единой терминологии служат целям упорядочения, исключения повторов в изложении материала, преемственности изложения и являются координирующими документами для преподавателей кафедр.

Пример согласования программных материалов физики и математики по семестрам приведен на схеме (указаны лишь некоторые темы курсов, информационный материал которых более всего нуждается в согласовании).

Как следует из схемы, к началу занятий по физике студентам необходимо изучить разделы математики, включая определенный интеграл и дифференциальные уравнения. При этом семестр по изучению математики является очень трудоемким для студентов, которые в школе на должном уровне не изучали элементы математики.

Приведем особо значимые для курса физики темы математики, иначе говоря, прямые программные связи курсов физики и математики.

В курсе высшей математики обращается особое внимание на:

1. изучение элементов векторной алгебры: понятие вектора, действия с векторами, производная вектора;
2. физический и геометрический смысл производных: нахождение производных тригонометрических, степенных и показательных функций (включая частные производные);
3. математические производные экстремумов;
4. элементы векторного анализа: ротор, дивергенция и градиент;
5. вычисление частного и полного дифференциала функций;
6. физический и геометрический смысл определенного интеграла; интегрирование тригонометрических, степенных, показательных и сложных функций, вычисление криволинейного интеграла и интеграла по поверхности;
7. линейные однородные и неоднородные дифференциальные уравнения первого и второго порядков;
8. разложение функций в ряд Тейлора и Фурье.

Решая задачи по физике с применением элементов математики, студенты должны обладать опытом использования математического аппарата (обратные связи):

1.1. Вычислять и изображать геометрически тригонометрические функции, площади круга, сектора, пользоваться радианными измерениями дуг и углов, использовать теорему косинусов.

1.2. Производить следующие действия над векторными величинами: сложение, вычитание, векторное умножение, скалярное умножение, дифференцирование и интегрирование векторных функций.

1.3. Оперировать элементами векторного анализа: вычислять градиент, дивергенцию и ротор характеристик векторных полей (запись с помощью векторного оператора «набла», объяснять и использовать теорему Стокса).

1.4. Находить производные тригонометрических, степенных и показательных функций, произведений функций и сложных функций. Объяснить физический и геометрический смысл производной.

1.5. Находить частные производные перечисленных функций нескольких переменных.

1.6. Вычислять экстремумы функций, а также графически изображать элементарные функции.

1.7. Вычислять частный и полный дифференциал функций.

1.8. Объяснять физический и геометрический смысл определенного интеграла, вычислять интегралы тригонометрических, степенных показательных, логарифмических функций, сложных функций, криволинейные интегралы и интегралы на поверхности.

1.9. Решать линейные однородные и неоднородные дифференциальные уравнения первого и второго порядков.

1.10. Разложить функцию в ряд Тейлора и Фурье.

После изучения курса физики студентам было предложено ответить на вопросы анкеты № 1 с целью выяснить влияние процесса согласования на результаты обучения данным дисциплинам. В анкетировании участвовало 20 студентов.

Анкета № 1

опроса студентов о влиянии на учебный процесс согласования межпредметных связей физики и математики

Проведенное анкетирование показало, что более 70% студентов отмечают усиление мотивации к изучению физики и математики, а также приобретение опыта решения задач по физике.

Большое влияние на успешность учебного процесса подготовки выпускника вуза оказывают междисциплинарные связи общепрофессиональных дисциплин с профессиональными [3]. Поскольку преподаватель знает направления и специальности студентов, которые обучаются в его потоке, он может, изучив рабочие программы профессиональных дисциплин, сообщить студентам, какие разделы изучаемой дисциплины окажут влияние на его профессиональную подготовку.

Очень полезно обсуждение межпредметных связей общепрофессиональных дисциплин с преподавателями профессиональных дисциплин [5]. В результате обсуждений формируются задания к курсам общепрофессиональных дисциплин.

В качестве примера приведены сформированные задания к курсу физики от курсов «Теория механизмов и машин» и «Теория резания и инструмент».

«Теория механизмов и машин»

При рассмотрении физических основ механики в курсе физики и решении задач студенты должны уметь:

1. Различать особенности поступательного и вращательного движений твердого тела на основе четких критериев.
2. Разлагать сложное движение твердого тела на поступательное и вращательное движение.
3. Строить структурно-логические схемы, указывающие на связи между линейными и угловыми характеристиками вращения твердого тела.
4. Использовать на практике законы Ньютона для поступательного движения твердого тела.
5. Формулировать и применять для решения задач основной закон вращения твердого тела (связь между суммарным моментом действующих сил, моментом инерции и угловым ускорением).
6. Определять в конкретных случаях силы трения и сопротивления при движении в некоторой среде.

«Теория резания и инструмент»

В курсе физики изучаются вопросы:

1. типы связей в кристаллических диэлектриках, полупроводниках и металлах, особенности металлической связи;
2. элементы теории структурных несовершенств в кристаллах (точечные дефекты и линейные несовершенства: краевые, винтовые и смешанные дислокации);
3. упругие свойства дислокаций (поле напряжений от дислокаций и энергия дислокаций);
4. механизмы пластической деформации на основе теории дислокаций;
5. особенности пластической деформации поликристаллов (влияние границ зерен на процесс деформации, локальность деформаций в поликристаллах, зависимость деформации от вида решеток);
6. современные методы обработки поверхности различных металлов: модификация поверхностей непрерывными и импульсными ионными пучками; ионно- и газоплазменное напыление.

После изучения физики студентам было предложено ответить на вопросы анкеты № 2.

Анкета № 2,п озволяющая оценить отношение студентов к согласованию программы физики с профессиональными дисциплинами

1. Было ли Вам интересно на лекциях и практических занятиях по физике?

• Да, потому что понимал.
• Да, потому что уловил связь с профессией.
• Нет.
• Затрудняюсь с ответом.

2. Почувствовали ли Вы заинтересованность преподавателя в том, чтобы Вы стали профессионалами?

• Да, конечно.
• Да, в какой-то мере.
• Скорей всего нет.
• Нет.

3. Преподаватель указывал, какой материал использовался в спец. курсах?

• Да.
• Да, в какой-то мере.
• Скорей всего нет.
• Нет.

4. Была ли понятна связь дисциплины с будущей профессией?

• Да, вполне.
• Да, в основном.
• Почти непонятна.
• Нет.

Анализ результатов анкетирования показал, что в среднем более 80% студентов удовлетворены процессом обучения, в котором учтены межпредметные связи физики с профессиональными дисциплинами.

Таким образом, учет междисциплинарных связей физики и математики, а также связь физики с профессиональными дисциплинами повышают мотивацию к изучению физики и математики и в конечном счете повышают эффективность подготовки выпускников вуза.