Линия уравнений и неравенств является одной из основных линий школьного курса математики. От успешности усвоения ее содержания зависит и успешность овладения учащимися различными разделами, как школьного курса математики, так и курсом высшей математики. Анализируя содержание учебного материала курса алгебры основной школы на предмет изложения в нем вопросов, связанных с числовыми неравенствами и их свойствами, важно отметить, что, не смотря на то, что отношения «больше» и «меньше» на интуитивном уровне формируются у обучающихся уже в начальной школе, определение этих отношений и их свойства изучаются только в 8 классе. Это обусловлено определенными трудностями, которые вытекают из особенностей, свойств и, как следствие преобразований неравенств.
В курсе алгебры 8 класса вводится следующее определение понятий «больше» и «меньше» для чисел: «число а больше числа в, если разность чисел а-в - число положительное; число а меньше числа в, если разность чисел а-в - число отрицательное», на основании которого можно работать только с неравенствами, в которых знаком «больше» или «меньше» связаны только два числа (или выражения). Далее изучаются следующие свойства числовых неравенств:
1. Если 
. Если 
;
2. Если 
;
3. Если 
;
4. Если 
. Если 
;
5. Если 
;
6. Если 
;
7. Если 
;
8. Если 
.
На основании определения и перечисленных свойств можно выполнять некоторые операции над неравенствами: умножение обеих частей на число, знак которого известен, сложение неравенств одного знака, умножение неравенств при определенных условиях и т.д. Они так же используются при доказательстве числовых неравенств [3] и в дальнейшем, позволяют выполнять равносильные преобразования при решении неравенств с одной переменной и исследовать свойства функций.
Однако, применение определения и вышеуказанных свойств для работы с числовыми неравенствами, в школьном курсе алгебры, ограничивается преимущественно только рамками данной темы. Так же важно отметить, что двойные неравенства из рассмотрения практически исключаются. В школьном курсе алгебры они используются для записи числовых промежутков, или для оценки значений функции. Поэтому целью нашего исследования является изучение возможности расширения данной темы на примере работы с двойными числовыми неравенствами. Для этого приведем анализ двойных неравенств, используя свойства линейной функции и обратной пропорциональности, тем самым показывая связь линии уравнений и неравенств с функциональной линией курса алгебры основной школы.
Этот подход мы использовали на занятиях в физико-математической школе «Омега» при КГУ им. К.Э. Циолковского мы использовали для анализа двойных неравенств. Он заключался в использовании свойства монотонности ограниченных функций на данном отрезке. Приведем рассуждения о свойствах неравенств с позиции функционального подхода.
Пусть 
и пусть рассматривается операция 
, где 
либо «+», либо «-», либо «
». Требуется установить тот промежуток, в котором лежит . Для этого необходимо установить левую и правую границы промежутка. Рассмотрим при фиксированном значении
следующие функции: 
, 
, 
. Они являются монотонными, поэтому их наибольшее и наименьшее значения достигаются на концах промежутка для переменной 
, т.е. в точках либо 
, либо 
. Зафиксировав значение и проводя аналогичные рассуждения относительно переменной , приходим к выводу, что наибольшее и наименьшее значения указанных функций достигаются на концах промежутка 
. Таким образом, для решения вопроса о границах промежутка, необходимо оценить четыре соотношения 
, 
, 
, 
. Самое большое из них будет правой границей искомого промежутка, а самое маленькое – левой.
Рассмотрим отдельно каждую из выше обозначенных функций. В случае
операции «+» функция монотонно возрастает как относительно при фиксированном , так и относительно при фиксированном (является линейной с угловым коэффициентом k равным 1 как для аргумента , так и для аргумента ). Поэтому наибольшее значение функции будет 
, а наименьшее 
. Таким образом, получаем промежуток 
. Получившееся неравенство является следствием свойства 6, применимо к двойным неравенствам.
В случае операции «-», функция монотонно возрастает относительно переменной при фиксированном (то есть является линейной с угловым коэффициентом k равным 1). И монотонно убывает относительно переменной , при фиксированном (линейная с угловым коэффициентом k равным -1). Поэтому наибольшее значение функция будет принимать при наибольшем значении и наименьшем значении , а наименьшее - при наименьшем и наибольшем . Таким образом, получаем промежуток 
. С другой стороны, используя вышеописанные свойства, применительно к двойным неравенствам получаем следующую цепочку неравенств: 
.
В случае операции «
» функция возрастает относительно х при фиксированном положительном значении у (линейная с положительным угловым коэффициентом) и убывает при фиксированном отрицательном значении у (линейная, с отрицательным угловым коэффициентом). Аналогичные рассуждения проводим для данной функции относительно переменной у при фиксированном значении х разных знаков. Таким образом, можно сделать вывод, что эта функция может принимать наибольшее положительное значение, как при положительных, так и при отрицательных значениях переменных х и у, и эти значения будут определяться наибольшим и наименьшим значениями чисел 
, 
, 
, 
.
Рассмотрим произведение , как произведение модулей этих величин, 
, как при 
и
, так и при 
и 
. Поэтому в данном случае наибольшее и наименьшее значение произведения будет находиться как 
, 
.
Рассмотрим некоторые частные случаи:
1) 
,
;
Данное неравенство получается как следствие использования свойства 7 применительно к двойным неравенствам. Однако, данное свойство справедливо только для положительных границ неравенства, поэтому остальные случаи для границ неравенства требуют отдельного рассмотрения.
2) 
,
;
3) 
,
.
Теперь рассмотрим операцию деления, то есть 
. Данное отношение можно преобразовать, сведя операцию деления к операции умножения: 
. При этом в случае, когда 
, а когда 
. Функция возрастает относительно х при фиксированном положительном значении у (линейная с положительным угловым коэффициентом) и убывает при фиксированном отрицательном значении у (линейная с отрицательным угловым коэффициентом). Относительно переменной у при фиксированном положительном значении х данная функция убывает (обратная пропорциональность с положительным коэффициентом) и возрастает при отрицательном значении х (обратная пропорциональность с отрицательным коэффициентом). Следовательно, ее наибольшее и наименьшее значения находим среди чисел 
.
Особого рассмотрения требует случай, когда одна из границ промежутка для переменной у равна нулю. Если промежуток замкнутый относительно нуля (нестрогое неравенство), то один из концов промежутка будет не определен (деление на нуль). Если промежуток открытый относительно нуля, то используя идею предельного перехода, можно определить значения функции на концах промежутка. Например, если 
, 
, то 
; если 
то 
. Таким, образом, в процессе изучения данной темы на интуитивном уровне осуществляется пропедевтика одного из основных понятий математического анализа как предел функции в точке.
Таким образом, проведенный анализ позволяет определить интервал, которому будет принадлежать выражение, представляющее сумму, разность, произведение или частное монотонных функций определенных на данном промежутке, с одной стороны, с другой стороны позволяет выполнять выше обозначенные операции над двойными неравенствами. Использованный теоретический материал не выходит за рамки курса алгебры основной школы, так как линейная функция и функция обратная пропорциональность изучаются в 7 и 8 классах, и дает возможность для расширения и углубления темы «Числовые неравенства».
Приведем некоторые задания для учащихся, иллюстрирующие возможность применения описанных теоретических рассуждений.
На первом этапе работы с двойными неравенствами учащимся могут быть предложены следующие задания:
1) оценить значение выражения 
2) оценить значение выражения 
3) оценить значение выражения 
4) оценить значение выражения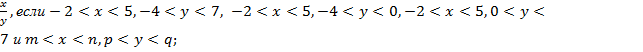 
При этом нужно разобрать случаи с различными по знаку значениями на концах промежутков, для строгих и нестрогих неравенств и, решая четвертое задание в общем виде наложить условия на границы.
5) каким неравенством связаны концы промежутка для переменной х и ноль, если 
6) каким неравенством связаны концы промежутка для переменной y и ноль, если 
В процессе решения таких заданий с одной стороны важным является их анализ, как с позиции известных учащимся свойств числовых неравенств, так и с позиции использования свойств функций для оценки выражений.
Умение работать с двойными неравенствами позволяет решать задачи, связанные с оценкой различных величин. Приведем пример такого задания.
Пример1. Найти целую часть числа
Решение. Воспользуемся неравенствами
.
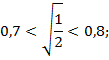
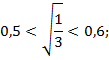
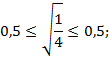
(они получаются при извлечении корней с точностью до 0,1 с недостатком и избытком). Складывая эти неравенства, получаем
Обобщением данной задачи является следующий пример.
Пример 2. Найти целую часть числа
Навыки, сформированные у учащихся в процессе изучения данной темы, могут быть использованы при изучении функциональной линии, то есть при решении задач на нахождение области значений функции, представляющей собой сумму, произведение или частной функций, монотонных на заданном промежутке.
В основной школе учащимся могут быть предложены следующие задания: оценить значение выражений 
В старшей школе учащимся могут быть предложены аналогичные задания, с использованием трансцендентных функций.
Также важно отметить, что оценка двойных неравенств в общем виде позволяет осуществлять подготовку учащихся к решению задач с параметрами.
Рецензенты:
Кристя В.И., д.ф.-м.н., профессор кафедры «Высшая математика» КФ МГТУ им. Н.Э. Баумана , г. Калуга;
Щербатых С.В., д.п.н., доцент, проректор по учебной работе, профессор кафедры «Математика и методика ее преподавания» ФГБОУ ВПО «Елецкий государственный университет им. И.А. Бунина», г. Елец.