Моделирование эксперимента в условиях неопределенности является одной из центральных проблем при исследовании технических систем и тесно связано с теорией, положенной в основу модели. Одной из составляющих неопределенности эксперимента является неопределенность измерения, которая состоит из двух компонент: неопределенность категории А и категории В [9]. Если к категории А относят объективные вероятностные оценки ряда измерений, то при поиске компонентов категории В возможно использование субъективных знаний, формализованных с применением теории нечетких множеств [6]. Растущие требования к точности результатов удовлетворяются не только за счет применения прецизионных приборов, но и путем использования методов мягких вычислений и измерений.
Модели эксперимента
Рассмотрим модели эксперимента, отражающие различные стороны неопределенности.
Неопределенность эксперимента, связанную со случайным характером проведения измерений, воздействием внешней среды и других факторов, можно отразить в рамках вероятностной модели эксперимента. Как известно, классической моделью эксперимента является аксиоматическая трактовка А.Н. Колмогорова в виде вероятностного пространства
![]() , (1)
, (1)
где ![]() – множество элементарных событий или исходов эксперимента;
– множество элементарных событий или исходов эксперимента;
![]() -
- ![]() – алгебра подмножеств
– алгебра подмножеств ![]() ;
; ![]() – вероятность на
– вероятность на ![]() [7].
[7].
Дальнейшим развитием вероятностной модели (1) является предложенная в [1,3] модель активного эксперимента в пространстве состояний, которая имеет вид
![]() , (2)
, (2)
где ![]() – дискретное вероятностное пространство с соответствующей
– дискретное вероятностное пространство с соответствующей ![]() -алгеброй
-алгеброй![]() , в котором определено пространство состояний S
, в котором определено пространство состояний S![]() , как подмножество множества всех пар вершин
, как подмножество множества всех пар вершин ![]() и подпространств в
и подпространств в ![]() .
.
Знание вероятностей ![]() позволяет нам вести оптимизацию по различным критериям, как энтропия эксперимента или энергозатраты [1,2,5]. Однако точечные оценки вероятностей реально часто являются недосягаемыми в силу различных ограничений.
позволяет нам вести оптимизацию по различным критериям, как энтропия эксперимента или энергозатраты [1,2,5]. Однако точечные оценки вероятностей реально часто являются недосягаемыми в силу различных ограничений.
В последнее время наблюдается интерес к применению теории нечетких множеств для описания неточности и нечеткости сложных технических объектов [6]. Нечеткая модель эксперимента на основе FN-чисел предложена в работе [1,3]:
![]() (3)
(3)
где![]() – алгебраическая система с одной определяющей операцией;
– алгебраическая система с одной определяющей операцией;
![]() – дискретное пространство
– дискретное пространство ![]() с заданным отношением
с заданным отношением ![]() ;
;
![]() – арифметика
– арифметика ![]() -чисел на множестве оценок
-чисел на множестве оценок ![]() с функцией стоимости
с функцией стоимости ![]() , определяемое конкретной задачей, например, нечеткая оптимизация по энергозатратам [4].
, определяемое конкретной задачей, например, нечеткая оптимизация по энергозатратам [4].
Традиционной теории нечетких множеств Заде присущи ограничения, так как учитывается только область, ограниченная функцией принадлежности. Это означает необходимость перехода к новым базовым семантикам принадлежности.
Для заполнения пробела в области структуризованной неопределенности там, где нельзя корректно применять статистические методы, можно использовать расширения теории нечетких множеств, либо комбинировать нечеткость и вероятность.
Интуиционистские нечеткие множества
Концепция интуиционистского нечеткого множества (IFS) как расширение нечеткого множества была выдвинута К. Атанассовым [8].
Определение 1. Интуиционистским нечетким множеством В называют множество вида
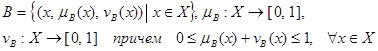 , (4)
, (4)
где![]() – соответственно функции принадлежности и непринадлежности произвольного элемента
– соответственно функции принадлежности и непринадлежности произвольного элемента ![]() множесту Х. Для каждого IFS можно определить интуиционистский индекс нечеткости
множесту Х. Для каждого IFS можно определить интуиционистский индекс нечеткости ![]() .
.
Определены следующие операции для IFS А и В.
Определение 2. Оператор объединения ![]() между А и В задается:
между А и В задается:
![]()
Определение 3. Оператор пересечения ![]() между А и В задается:
между А и В задается:
![]()
Определение 4. Дополнение множества А определяется:
![]() .
.
Фаззификация задачи эксперимента
Для реализации вероятностной модели эксперимента необходимо знание исходного распределения вероятностей ![]() . При отсутствии такой оценки на ранних стадиях эксперимента применим эмпирическую или теоретическую оценку степени принадлежности и непринадлежности вероятности
. При отсутствии такой оценки на ранних стадиях эксперимента применим эмпирическую или теоретическую оценку степени принадлежности и непринадлежности вероятности ![]() -гипотезы с помощью соответствующих функций
-гипотезы с помощью соответствующих функций ![]() в рамках следующей задачи.
в рамках следующей задачи.
Задача 1. Пусть относительно объекта исследований выдвинута группа из ![]() - гипотез
- гипотез![]() с функциями
с функциями ![]() . Также определено множество допустимых экспериментов
. Также определено множество допустимых экспериментов ![]() по верификации гипотез и соответствующие стоимости их проведения
по верификации гипотез и соответствующие стоимости их проведения ![]() . Требуется оптимизировать процесс экспериментального подтверждения одной из гипотез
. Требуется оптимизировать процесс экспериментального подтверждения одной из гипотез ![]() с оценкой надежности результатов моделирования.
с оценкой надежности результатов моделирования.
Отличием такой постановки от вероятностного подхода является то, что условие несовместности и ограничения теории вероятностей могут не выполняться.
Используя априорные знания о неопределенности измерения, проводим фаззификацию задачи эксперимента. В данной работе в качестве ![]() предлагается использовать унимодальные нечеткие
предлагается использовать унимодальные нечеткие![]() -числа (треугольные), так как они более адекватно оценивают высказывания типа «вероятность гипотезы приблизительно равна 0,5», а в качестве
-числа (треугольные), так как они более адекватно оценивают высказывания типа «вероятность гипотезы приблизительно равна 0,5», а в качестве ![]() – толерантные (трапециевидные) числа (более приближены к реальности). Функции
– толерантные (трапециевидные) числа (более приближены к реальности). Функции ![]() ,
, ![]()
![]() -чисел приведены в модифицированном LR-формате, который выбирается из условия минимума отклонения от нормального закона.
-чисел приведены в модифицированном LR-формате, который выбирается из условия минимума отклонения от нормального закона.
Аналитически ![]() записывается следующим образом:
записывается следующим образом:
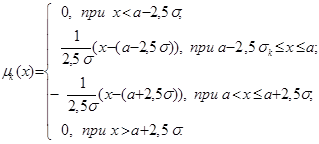 (6)
(6)
Соответственно для ![]() выражение в LR-формате выглядит (трапециевидная форма):
выражение в LR-формате выглядит (трапециевидная форма):
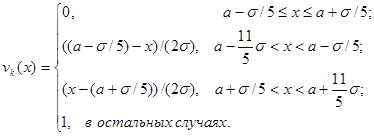 (7)
(7)
Определение 5. Нечеткие числа, функция принадлежности которых имеет график в форме равнобедренного треугольника (трапеции), отнесем к нечетким естественным числам (![]() -числа) и будем записывать в виде
-числа) и будем записывать в виде ![]() , где
, где ![]() – мода
– мода ![]() -числа, усредненное значение );
-числа, усредненное значение ); ![]() ,
, ![]() – среднеквадратичное отклонение оценки.
– среднеквадратичное отклонение оценки.
Особенностью использования ![]() -чисел для оценки вероятностей заключается в том, что они наглядно отражают связь между оцениваемой величиной, возможной погрешностью и позволяют достаточно корректно ими оперировать в рамках поставленной задачи. Основные операции
-чисел для оценки вероятностей заключается в том, что они наглядно отражают связь между оцениваемой величиной, возможной погрешностью и позволяют достаточно корректно ими оперировать в рамках поставленной задачи. Основные операции![]() для
для ![]() -чисел приведены в [4].
-чисел приведены в [4].
Определение 6. Нечетким множеством оценок ![]() (IFS-оценки) назовем:
(IFS-оценки) назовем:
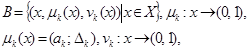 . (8)
. (8)
на котором определена ![]() -арифметика нечетких чисел
-арифметика нечетких чисел![]() .
.
Модель эксперимента на основе интуиционистских нечетких множеств
Пусть ![]() дискретное пространство состояний с заданным отношением
дискретное пространство состояний с заданным отношением ![]() . Введем в нечеткую модель (4) IFS-оценки
. Введем в нечеткую модель (4) IFS-оценки
![]() (9)
(9)
где![]() – алгебраическая система с одной определяющей операцией;
– алгебраическая система с одной определяющей операцией;
![]() – дискретное пространство
– дискретное пространство![]() с заданным отношением
с заданным отношением![]() ;
;
![]() -
-![]() -арифметика
-арифметика ![]() -чисел на множестве В с функцией стоимости
-чисел на множестве В с функцией стоимости ![]() , определяемое конкретной задачей .
, определяемое конкретной задачей .
В качестве ![]() могут использоваться различные критерии эксперимента: стоимость, время, энергозатраты, сложность, нечеткая энтропия, достоверность.
могут использоваться различные критерии эксперимента: стоимость, время, энергозатраты, сложность, нечеткая энтропия, достоверность.
Любому антисимметричному нечеткому отношению ![]() можно поставить в соответствие один (и только один) обычный антисимметричный граф
можно поставить в соответствие один (и только один) обычный антисимметричный граф ![]() . Такое отношение можно показать на плоскости взвешенным графом с матрицей отношений
. Такое отношение можно показать на плоскости взвешенным графом с матрицей отношений ![]() , в котором каждая пара вершин
, в котором каждая пара вершин ![]() соeдиняется стрелкой с весом
соeдиняется стрелкой с весом ![]() , рис.1.
, рис.1.
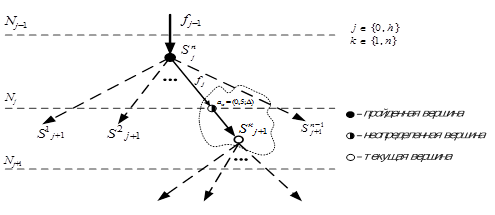
Рис. 1. Поиск в пространстве S при нечетком подходе
Неопределенность, возникающую в процессе проведения эксперимента, введем появлением в последовательности координатой ![]() – «состояние не определено», рис. 1.
– «состояние не определено», рис. 1.
Будем учитывать особенности процесса эксперимента. Если в результате ![]() -эксперимента отвергнута гипотеза
-эксперимента отвергнута гипотеза ![]() , (произошло событие
, (произошло событие ![]() ), то вследствие теоремы Байеса получаем апостериорные (поисковые) оценки вероятностей гипотез
), то вследствие теоремы Байеса получаем апостериорные (поисковые) оценки вероятностей гипотез ![]() :
:
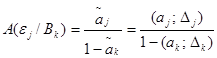 . (10)
. (10)
Модель (9) позволяет по мере набора статистического материала осуществить переход к вероятностной модели. После проведения ![]() определяются количественные значения
определяются количественные значения ![]() и направление поиска.
и направление поиска.
Возникает вопрос, до какого момента можно доверять интуиционистскому моделированию? Какова надежность подтверждения гипотезы?
Надежность подтверждения гипотезы
Пусть будет проведена серия из ![]() -экспериментов для статистического подтверждения одной из
-экспериментов для статистического подтверждения одной из ![]() -гипотез,
-гипотез, ![]() . В основу пересчета распределения оценок вероятностей В после каждой серии положим следующий принцип. Оценки вероятностей гипотез рассмотрим как веса вершин стандартного симплекса, рис. 2. Тогда априорное распределение оценок вероятностей гипотез
. В основу пересчета распределения оценок вероятностей В после каждой серии положим следующий принцип. Оценки вероятностей гипотез рассмотрим как веса вершин стандартного симплекса, рис. 2. Тогда априорное распределение оценок вероятностей гипотез ![]() будет определять центр тяжести симплекса. После серии экспериментов центр тяжести симплекса переместится в точку
будет определять центр тяжести симплекса. После серии экспериментов центр тяжести симплекса переместится в точку ![]() , апостериорное распределение оценок будет в случае подтверждения
, апостериорное распределение оценок будет в случае подтверждения ![]() -ой гипотезы
-ой гипотезы
![]() (11)
(11)
что изображено на рис.3 для случая ![]() .
.
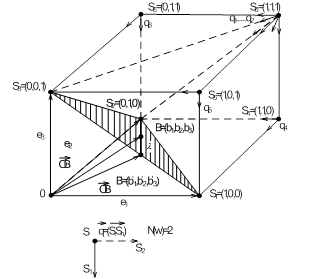
Рис. 2. Представление симплекса В в S
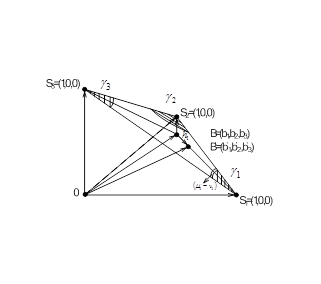
Рис. 3. Апостериорное распределение оценок ![]()
На симплексе ![]() можно выбрать замкнутые и выпуклые множества
можно выбрать замкнутые и выпуклые множества ![]() , не зависящих от априорного распределения
, не зависящих от априорного распределения ![]() . При попадании распределения
. При попадании распределения ![]() в одно из множеств
в одно из множеств ![]() принимается окончательное решение о принятии гипотезы. Выработаем соответствующее решающее правило. После каждой серии экспериментов
принимается окончательное решение о принятии гипотезы. Выработаем соответствующее решающее правило. После каждой серии экспериментов ![]() определяется точка
определяется точка ![]() на симплексе
на симплексе ![]() . Эксперименты продолжаются до тех пор, пока
. Эксперименты продолжаются до тех пор, пока ![]() не попадет в одно из множеств
не попадет в одно из множеств ![]() . Если
. Если ![]() попадает внутрь области
попадает внутрь области ![]() , эксперимент прекращается и принимается решение
, эксперимент прекращается и принимается решение ![]() , где
, где ![]() – номер подтвержденной гипотезы. Если
– номер подтвержденной гипотезы. Если ![]() попадает в область
попадает в область ![]() , вопрос о прекращении эксперимента и принятии окончательного решения или о продолжении решается при помощи независимого случайного механизма.
, вопрос о прекращении эксперимента и принятии окончательного решения или о продолжении решается при помощи независимого случайного механизма.
Построим множества ![]() исходя из понятия надежности гипотезы. Надежностью гипотезы назовем
исходя из понятия надежности гипотезы. Надежностью гипотезы назовем
![]() (12)
(12)
- минимальный уровень значимости, при котором ![]() принадлежит множеству
принадлежит множеству ![]() . Выпуклые и замкнутые множества
. Выпуклые и замкнутые множества ![]() при вершинах стандартного симплекса могут быть заданы условиями, исходя из обычной метрики в пространстве состояний
при вершинах стандартного симплекса могут быть заданы условиями, исходя из обычной метрики в пространстве состояний ![]()
![]() (13)
(13)
где ![]() , где
, где ![]() – малое положительное число.
– малое положительное число.
Если неравенство (13) выполняется, то мы должны принять гипотезу, а если нет, то отвергнуть. Критерий (13) обычно носит название критерия значимости гипотезы, а число ![]() , которое выступает в роли предельной оценки вероятности, называется уровнем значимости критерия или коэффициентом доверия (надежности).
, которое выступает в роли предельной оценки вероятности, называется уровнем значимости критерия или коэффициентом доверия (надежности).
Заключение
Таким образом, применение IFS вместо нечетких множеств означает введение дополнительных степеней свободы. Такое обобщение нечетких множеств дает нам дополнительную возможность представления недостаточных знаний о том, что лежит в описании многих действительных проблем эксперимента.
Нечетко-вероятностная модель эксперимента позволяет выбрать наилучшее представление и формулировать задачу эксперимента в зависимости от уровня знаний об объекте исследований, в нашем случае о теории, которой должна стать одна из гипотез. Принятие гипотезы связано с критерием ![]() , то есть коэффициентом доверия (надежности).
, то есть коэффициентом доверия (надежности).
Рецензенты:
Чаткин М.Н. д.т.н., профессор, ректор ФГБОУ «Мордовский институт переподготовки кадров агробизнеса», г. Саранск;
Щенников В.Н., д.ф-м.н., профессор ФГБОУ ВПО «МГУ им. Н.П. Огарева, г. Саранск.



