Задача о притоке реального газа к несовершенной скважине при нелинейном законе фильтрации является весьма сложной и до сих пор не получила точного аналитического решения. В работах Е.М. Минского, А.Е. Хейна, Г.А. Зотова, С.М. Тверковкина и др. рассматривалась данная задача в приближенной постановке. Здесь рассматривается задача о притоке реального газа к несовершенной скважине в однородно-анизотропном пласте, т. е. с учетом анизотропии, а также предлагается несколько иной подход к расчету фильтрационных сопротивлений, обусловленных несовершенством скважины по степени вскрытия.
В работе Е.М. Минского [1] показано, что коэффициент фильтрационного сопротивления как при линейном, так и при квадратичном законе фильтрации зависит только от геометрии потока. В связи с этим к выводу уравнения притока газа можно подойти следующим образом. Для нелинейного закона фильтрации имеем уравнение
![]() (1)
(1)
где
![]() – плотность газа.
– плотность газа.
Геометрия потока, очевидно, будет определяться функцией ![]() в области пространственного потока
в области пространственного потока ![]() (рисунок 1). Вся трудность решения состоит в нахождении уравнения кривой
(рисунок 1). Вся трудность решения состоит в нахождении уравнения кривой ![]() , ограничивающей область потока, или, другими словами, уравнения линии тока. Размер зоны пространственного движения будет зависеть от многих факторов, например, не только от геометрии пласта (
, ограничивающей область потока, или, другими словами, уравнения линии тока. Размер зоны пространственного движения будет зависеть от многих факторов, например, не только от геометрии пласта (![]() ,
, ![]() ,
, ![]() ), но и от анизотропии пласта æ*, дебита
), но и от анизотропии пласта æ*, дебита ![]() , градиента давления (
, градиента давления (![]() ) и т. д. Следуя И.А. Чарному [5], примем радиус зоны пространственного притока
) и т. д. Следуя И.А. Чарному [5], примем радиус зоны пространственного притока ![]() . Будем аппроксимировать упомянутую линию тока уравнением вида [4]
. Будем аппроксимировать упомянутую линию тока уравнением вида [4]
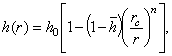 (2)
(2)
где
![]()
![]()
![]() – некоторая функция, зависящая от несовершенства скважины по степени вскрытия, геометрии пласта и скважины, анизотропии пласта.
– некоторая функция, зависящая от несовершенства скважины по степени вскрытия, геометрии пласта и скважины, анизотропии пласта.
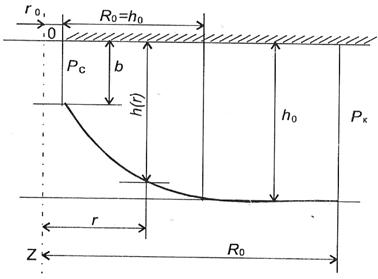
Рис.1. Двухзонная схема притока газа к несовершенной скважине при нелинейном законе фильтрации
Умножая левую и правую части уравнения (1) на ![]() , применяя двухзонную схему притока (см. рисунок 1), учитывая уравнение состояния реального газа, уравнение (2) и интегрируя в соответствующих пределах по давлению и радиусу, после некоторых преобразований получаем известную двучленную формулу притока:
, применяя двухзонную схему притока (см. рисунок 1), учитывая уравнение состояния реального газа, уравнение (2) и интегрируя в соответствующих пределах по давлению и радиусу, после некоторых преобразований получаем известную двучленную формулу притока:
![]() (3)
(3)
где
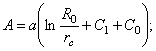 (4)
(4)
![]() (5)
(5)
![]() ;
; ![]()
![]()
![]() (6)
(6)
![]() ;
; 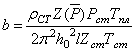 . (7)
. (7)
Выражение для ![]() представляется сложной функцией, выраженной суммой рядов от 1 до
представляется сложной функцией, выраженной суммой рядов от 1 до ![]() и зависящей от параметров
и зависящей от параметров ![]()
![]()
![]() и
и ![]()
![]() [4], где
[4], где
![]()
![]() ;
; ![]() ;
; 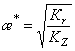 . (8)
. (8)
Коэффициент фильтрационного сопротивления ![]() , обусловленный относительным вскрытием пласта
, обусловленный относительным вскрытием пласта ![]() , определяется формулой [2]
, определяется формулой [2]
![]() (9)
(9)
где
![]() – некоторая функция, связанная с распределением потенциала скорости фильтрации, вызванного работой несовершенной скважины, рассчитана на ЭВМ, затабулирована и представлена графиками (рисунок 2).
– некоторая функция, связанная с распределением потенциала скорости фильтрации, вызванного работой несовершенной скважины, рассчитана на ЭВМ, затабулирована и представлена графиками (рисунок 2).
Из совместного решения (6) и (9) определена функция ![]() , рассчитана на ЭВМ, затабулирована в широком диапазоне параметров и представлена графическими зависимостями (рисунок 2). При найденных значениях
, рассчитана на ЭВМ, затабулирована в широком диапазоне параметров и представлена графическими зависимостями (рисунок 2). При найденных значениях ![]() функция
функция ![]() , также была рассчитана на ЭВМ в широком диапазоне параметров и затабулирована.
, также была рассчитана на ЭВМ в широком диапазоне параметров и затабулирована.
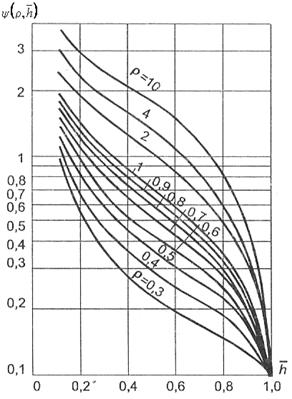
Рис.2. Зависимость функции ![]() , связанной со средним значением потенциала скважины, от относительного вскрытия пласта
, связанной со средним значением потенциала скважины, от относительного вскрытия пласта ![]()
Методика расчета безводных дебитов в случае притока реального газа к несовершенной скважине по нелинейному закону фильтрации при наличии подошвенной воды рассматривалась в работе [6]. Однако сама задача о предельных безводных дебитах в точной постановке не решена из-за того, что не известно уравнение границы раздела двух жидкостей при наличии конуса подошвенной воды.
Приведем приближенное решение этой задачи, используя приближенное уравнение границы раздела, когда конус воды находится в предельно-устойчивом положении [2]:
![]() ;
; 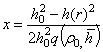 ;
; ![]() (10)
(10)
где
![]() – безразмерный предельный безводный дебит, определяемый по известным формулам, графикам или таблицам [2].
– безразмерный предельный безводный дебит, определяемый по известным формулам, графикам или таблицам [2].
Переменная толщина пласта, ограничивающая область пространственного притока, как это следует из (10), выражается формулой вида
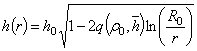 . (11)
. (11)
Умножая левую и правую части уравнения (1) на ![]() , учитывая, что объемный предельный дебит Q=Q0q(ρ0,
, учитывая, что объемный предельный дебит Q=Q0q(ρ0,![]() ) и (11), получаем формулу притока, выраженную через предельный безразмерный дебит, из которой легко определить предельную депрессию
) и (11), получаем формулу притока, выраженную через предельный безразмерный дебит, из которой легко определить предельную депрессию ![]()
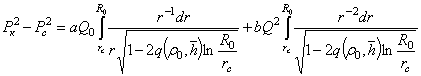 (12)
(12)
После интегрирования и некоторых преобразований уравнение притока примет вид (3), где A и В определяются по формулам (4) и (5), в которых коэффициенты представляются выражениями:
![]() ;
; ![]() ; (13)
; (13)
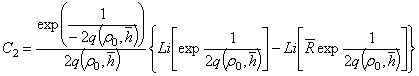 ; (14)
; (14)
где
![]() – коэффициент за счет перфорации,
– коэффициент за счет перфорации,
![]() – интегральный логарифм, который связан с интегральной показательной функцией
– интегральный логарифм, который связан с интегральной показательной функцией ![]() зависимостью
зависимостью
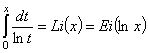 . (15)
. (15)
При ![]() >1 интеграл (15) расходится в точке
>1 интеграл (15) расходится в точке ![]() =1. В этом случае
=1. В этом случае ![]() представляет значение несобственного интеграла.
представляет значение несобственного интеграла.
Заметим, что из полученных формул притока для несовершенной скважины как частный случай вытекают формулы для линейного закона фильтрации.
Пример: Скважина работает при наличии устойчивого положения границ раздела. Исходные данные R0=1000 м; æ*=1; rс=0,1 м; h0=10 м; b=4 м. Тогда имеем следующие безразмерные параметры: ρ0=100; ![]() =0,4;
=0,4; ![]() =104. Требуется определить фильтрационные сопротивления, обусловленные наличием конуса воды.
=104. Требуется определить фильтрационные сопротивления, обусловленные наличием конуса воды.
По графикам [3] определяем безразмерный предельный безводный дебит: q(ρ0,![]() )=q(100;0,4)≈0,4. По формуле (13) находим
)=q(100;0,4)≈0,4. По формуле (13) находим ![]() ≈2,3 и по формуле (15) подсчитываем С2≈2,9. Как видим, значения
≈2,3 и по формуле (15) подсчитываем С2≈2,9. Как видим, значения ![]() и С2 оказались сравнительно небольшими, это объясняется тем, что предельный безводный дебит очень мал, а он и определяет геометрию потока, т. е. форму конуса подошвенной воды. После чего предельная депрессия
и С2 оказались сравнительно небольшими, это объясняется тем, что предельный безводный дебит очень мал, а он и определяет геометрию потока, т. е. форму конуса подошвенной воды. После чего предельная депрессия ![]() легко подсчитывается по формуле (12).
легко подсчитывается по формуле (12).
Рецензенты:
Грачев С.И., д.т.н., профессор, заведующий кафедрой «Разработка и эксплуатация нефтяных и газовых месторождений», Институт геологии и нефтегазодобычи, ФГБОУ ВПО ТюмГНГУ, г. Тюмень;
Леонтьев С.А., д.т.н., профессор, профессор кафедры «Разработка и эксплуатация нефтяных и газовых месторождений», Институт геологии и нефтегазодобычи, ФГБОУ ВПО ТюмГНГУ, г. Тюмень.



