При проведении наземных отработочных испытаний системы ориентации и стабилизации (СОС) перед разработчиками системы стоит задача в создании лабораторных комплексов для моделирования условий максимально приближенных к реальным условиям эксплуатации системы. При этом эффективность испытаний напрямую зависит от точности воспроизведения внешних воздействий. В настоящее время для решения задач наземных испытаний СОС, имеющей в своем составе позиционные приборы типа: прибор ориентации на Солнце (ПОС) или прибор ориентации на Землю (ПОЗ) и др., в АО ИСС созданы лабораторные комплексы, имитаторы и стенды [1], использующие методы как прямого, так и обращенного моделирования [4]. Широкое применение, из-за универсальности и простоты работы, получили лабораторные комплексы, построенные с использованием модульного типа, состоящие из двух или более функциональных единиц. Основной принцип, заложенный в создание таких комплексов, следующий: прибор, установленный на имитатор движения, совершает вращательное движение относительно опорного ориентира в соответствии с расчетными значениями, аналогичных угловому движению космического аппарата.
В данной статье рассматривается актуальный вопрос обеспечения точности задания входных воздействий на прибор ориентации на Солнце при проведении динамических испытаний СОС. Целью статьи является разработка методики расчета управляющих воздействий для управления лабораторным комплексом, предназначенного для имитации углового отклонения прибора ПОС относительно ориентира (имитатора Солнца).
На рисунке 1 представлена функциональная схема построения лабораторного комплекса. Основными модулями лабораторного комплекса являются: имитатор Солнца и трехосной имитатор движения (ТИД), представляющий собой трехстепенный карданов подвес.
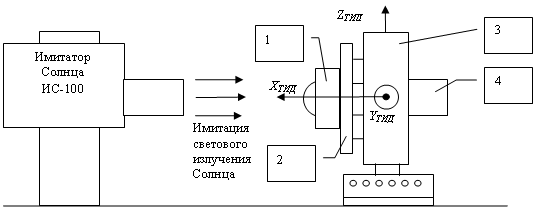
Рис. 1. Лабораторный комплекс
(где: 1 – прибор ориентации на Солнце; 2 – план – шайба (внутренняя ось); 3 – внешняя рамка ТИД; 4- промежуточная рамка ТИД; XТИД, YТИД, ZТИД – система координат (СК) ТИД)
Отсчет направляющих косинусов (НК) вектора направления на ориентир в системе координат ТИД и отсчет углов ТИД представлен на рисунке 2.
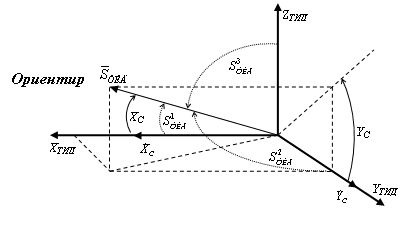
Рис. 2. Направление отсчета НК в СК ТИД
(где: XC,YC – текущие углы поворота рамок ТИД; ![]() – вектор направления на ориентир в СК ТИД;
– вектор направления на ориентир в СК ТИД; ![]() – компоненты (направляющие косинусы) вектора
– компоненты (направляющие косинусы) вектора ![]() )
)
В нулевом (исходном) положении компоненты вектора направления на ориентир в СК ТИД равны:
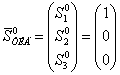 (1)
(1)
При двух поворотах вокруг осей XТИД и YТИД на углы XС и YС, компоненты вектора направления на ориентира в СК ТИД имеют вид:
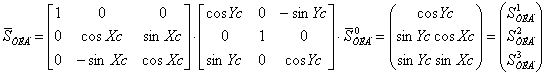 (2)
(2)
Разрешив уравнения (2), определим зависимость между углами поворота осей ТИД (XС,YС) и компонентами вектора направления на ориентир в СК ТИД:
![]() ;
; ![]() (3)
(3)
Взаимосвязь между вектором направления на ориентир в СК ТИД и вектором направления на ориентир в связанной системе координат (ССК) КА определяется как:
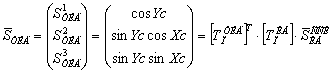 (4)
(4)
Где: ![]() – матрица установки ПОС на ТИД;
– матрица установки ПОС на ТИД;
![]() – матрица установки ПОС на КА;
– матрица установки ПОС на КА;
![]() – вектор направления на ориентир в ССК (система координат связанная с КА);
– вектор направления на ориентир в ССК (система координат связанная с КА);
![]() – вектор направления на ориентир в СК ТИД.
– вектор направления на ориентир в СК ТИД.
Определение приращения угла поворота рамок ТИД осуществляется следующим образом. За один шаг для малого приращения имеется:
![]() (5)
(5)
Для угла YС аналогично.
Где: XС(k), YС(k) – расчетное значение углов поворота рамок ТИД на k-том такте ;
XС(k+1), YС(k+1) – расчетное значение углов поворота рамок ТИД на k+1 такте;
ΔXС(k), ΔYС(k) – расчетное значение приращения углов поворота рамок ТИД.
Система уравнений с учетом (4) и (5) для векторов ![]() имеет вид:
имеет вид:
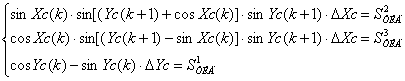 (6)
(6)
Искомое значения приращения углов ΔXС и ΔYС определяются разрешением системы уравнений (6) и равны:
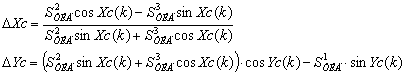 (7)
(7)
Тогда текущее значение угла поворота рамок ТИД и управляющее значение по скорости рассчитывается следующим образом:
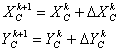 ;
; 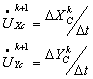 (8)
(8)
Где: Δt – дискретность моделирования (Δt = 0,25 с.).
k – такт расчета.
Для повышения точности воспроизведения углового положения ПОС относительно опорного ориентира разработана методика учета инструментальной погрешности, которая складывается из погрешности привязки (установки) прибора с посадочной плоскостью ТИД и погрешности выставки опорного ориентира относительно оси визирования прибора. Учет данной погрешности осуществляется путем использования поправочных коэффициентов, рассчитанных в результате анализа выходной характеристики ПОС, полученной при нулевом положении осей ТИД (в статическом состоянии) с помощью контрольно-проверочной аппаратуры.
Выходной информацией с ПОС является вектор направления на Солнце в приборной системе координат (ПСК), который определяется следующим образом:
![]() (9)
(9)
Где: ![]() – матрица перехода от ССК в СК прибора;
– матрица перехода от ССК в СК прибора;
![]() – вектор направления на ориентир в ПСК.
– вектор направления на ориентир в ПСК.
В свою очередь вектор ![]() определяется, как:
определяется, как:
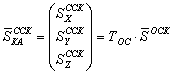 (10)
(10)
Где: ![]() – матрица перехода из орбитальной системы координат (ОСК) в связанную систему координат КА:
– матрица перехода из орбитальной системы координат (ОСК) в связанную систему координат КА:
![]() вектор направления на ориентир в ОСК.
вектор направления на ориентир в ОСК.
Для упрощения процедуры расчета поправочных коэффициентов примем матрицу ![]() равной единичной, тогда уравнение (10) примет вид:
равной единичной, тогда уравнение (10) примет вид:
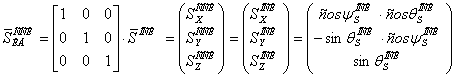 (11)
(11)
Где: ![]() – координаты ориентира в ОСК.
– координаты ориентира в ОСК.
Тогда с учетом (11) уравнение (4) примет вид:
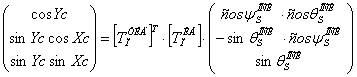 (12)
(12)
Откуда величина поправочных коэффициентов по углам поворота рамок ТИД будет равна:
![]() ;
; 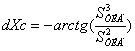 (13)
(13)
Таким образом, требуемое значение угла поворота рамок ТИД будет определяться как:
![]() ;
; ![]() (14)
(14)
С другой стороны, величину погрешности выставки ПОС относительно опорного ориентира возможно учитывать и при формировании вектора направления на ориентир в СК ТИД. Методика расчета и учета поправочного вектора следующая:
Шаг 1. Определяется теоретическое значение вектора направления на ориентир в СК ТИД, полагая, что инструментальная погрешность равна нулю:
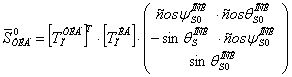 (15)
(15)
Где: ![]() – требуемое значение положения Солнца в ОСК, при котором вектор направления на Солнце в ПСК ПОС равен (1,0,0), т.е. ось визирования прибора направлена в центр опорного ориентира (Солнца);
– требуемое значение положения Солнца в ОСК, при котором вектор направления на Солнце в ПСК ПОС равен (1,0,0), т.е. ось визирования прибора направлена в центр опорного ориентира (Солнца);
![]() – расчетное значение вектора направления на опорный ориентир в СК ТИД, при нулевой инструментальной погрешности.
– расчетное значение вектора направления на опорный ориентир в СК ТИД, при нулевой инструментальной погрешности.
Шаг 2. Определяется текущее значение вектора направления на ориентир в СК ТИД с учетом инструментальной погрешности:
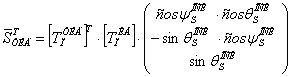 (16)
(16)
Где: ![]() – текущее значение положения Солнца в ОСК, рассчитанное по показаниям прибора ПОС;
– текущее значение положения Солнца в ОСК, рассчитанное по показаниям прибора ПОС;
![]() – текущее значение вектора направления на опорный ориентир в СК ТИД, рассчитанное по показаниям прибора ПОС.
– текущее значение вектора направления на опорный ориентир в СК ТИД, рассчитанное по показаниям прибора ПОС.
Шаг 3. Определяется поправочный вектор:
![]() (17)
(17)
Шаг 4. Учитываются поправки при формировании вектора направления на ориентир в СК ТИД:
![]() (18)
(18)
Оценка влияния погрешности вносимой лабораторным комплексом, а в частности трехосным имитатором движения, в процесс измерения динамических характеристик СОС проверена методом математического моделирования. Моделировались следующие процессы:
1) эталонный процесс динамики объекта (СОС) в начальном режиме ориентации на Солнце, без учета наземных условий (влияния испытательного оборудования);
2) процесс динамики объекта (СОС) на комплексе моделирующих стендов с введением лабораторного комплекса.
Оценка погрешности вносимой лабораторным комплексом, проведена путем сравнения результатов п.1) и 2).
Для анализа погрешностей использованы следующие модели: математическая модель СОС и математическая модель комплекса моделирующих стендов. При этом объектом исследования является математическая модель комплекса моделирующих стендов, а математическая модель СОС используется для ее замыкания.
Функциональная схема взаимодействия математических моделей в замкнутом контуре приведена на рисунке 3.
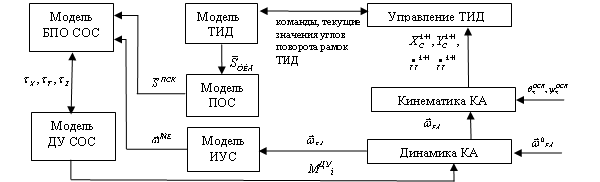
Рис. 3. Функциональная схема взаимодействия моделей в замкнутом контуре
(где: τX, τY, τZ – длительности включения двигателей, ![]() – вектор угловой скорости КА в системе координат ИУС,
– вектор угловой скорости КА в системе координат ИУС, ![]() – вектор абсолютной угловой скорости в системе координат КА, МДУi – момент создаваемый двигательной установкой (i = X, Y, Z);
– вектор абсолютной угловой скорости в системе координат КА, МДУi – момент создаваемый двигательной установкой (i = X, Y, Z); ![]() – углы определяющие положение Солнца в ОСК;
– углы определяющие положение Солнца в ОСК; ![]() – вектор направления на Солнце в системе координат ПОС;
– вектор направления на Солнце в системе координат ПОС; ![]() – вектор направления на опорный ориентир с системе координат ТИД;
– вектор направления на опорный ориентир с системе координат ТИД; ![]() – значение угла поворота рамок ТИД;
– значение угла поворота рамок ТИД; ![]() – скорость вращения рамок ТИД).
– скорость вращения рамок ТИД).
Математическая модель СОС предназначена для имитации функционирования аппаратуры СОС под воздействием управляющих и возмущающих воздействий в процессе углового движения КА относительно центра масс. Более подробно математическая модель СОС приведена в [3,5].
Модель СОС включала в себя:
1) Модель измерителя угловой скорости (ИУС), предназначенную для имитации измерения трех проекций угловой скорости на оси, связанной с прибором системы координат.
2) Модель ПОС, предназначенную для формирования управляющей информации об угловом положении центра Солнца в пределах поля обзора, имеющего значение от 0 до (91+0,5)° по углу α и значение от 0 до (181+0,5)° по углам β и γ.
3) Модель ДО, предназначенную для формирования управляющих моментов двигательной установкой по осям КА. Выходными параметрами модели являются моменты двигателей по осям КА.
4) Модель БПО СОС, предназначенную для моделирования логики функционирования системы, в частности функционирования системы в режиме начальной ориентации на Солнце.
Математическая модель комплекса моделирующих стендов предназначена для формирования управляющего воздействия на испытательное оборудование в соответствии угловым движения КА относительно центра масс. Модель комплекса моделирующих стендов включала в себя:
1) Математическую модель углового движения КА, представленную в виде динамики и кинематики КА, и представляет собой набор дифференциальных уравнений;
2) Модель управления ТИД, предназначенную для расчета и формирования управляющего воздействия на ТИД в соответствии с разработанным алгоритмом, приведенным выше.
3) Модель ТИД, в состав которой входят:
а) математическая модель привода ТИД, учитывающая коэффициент усиления и постоянную времени апериодического звена;
б) математическая модель датчика угла ТИД, с учетом люфтов на выходных валах ТИД и цены младшего разряда датчика;
в) математическая модель трехосного карданового подвеса, предназначенная для согласования и привязки модели привода ТИД с моделью прибора (ПОС) через матрицу установки на ТИД, и учитывающая погрешность неперпендикулярности осей ТИД и погрешность выставки опорного ориентира относительно оси визирования прибора.
Результаты моделирования эталонных переходных процессов и процессов с учетом погрешностей ТИД (на рис. обозначено как «Процесс_ТИД») представлены на рисунках 4–5, где показаны изменения углового положения Солнца в системе координат КА.
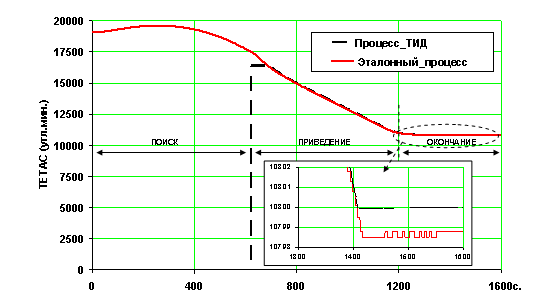
Рис. 4. Изменение углового положения Солнца в ССК по каналу тангажа
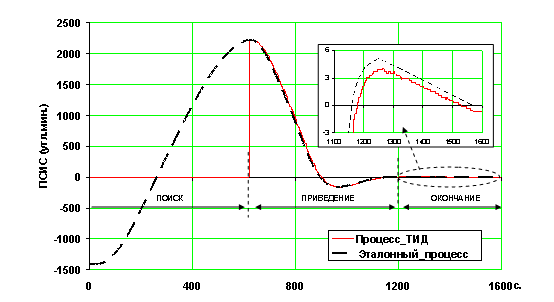
Рис. 5. Изменение углового положения Солнца в ССК по каналу рыскания
Моделирование эталонных переходных процессов проводилось интегрированием общей системы дифференциальных уравнений с шагом 50 мс. В общую систему дифференциальных уравнений включались уравнение динамики и кинематические уравнения объекта. При моделировании переходных процессов с учетом погрешностей лабораторного комплекса в общей системе дифференциальных уравнений интегрировались уравнения динамики приводов ТИД с шагом 250 мс, уравнения динамики и кинематики объекта с шагом 50 мс. Анализ результатов моделирования показал, что погрешности воспроизведения (примерно 90 % ошибки) в основном определяются:
- несоостностью плоскопараллельного светового пучка имитатора Солнца с посадочным местом (центром план-шайбы ТИД);
- точностью калибровочной выставки центра поля зрения испытуемого прибора с плоскопараллельным световым пучком имитатора Солнца.
Погрешность, вызванная тактом интегрирования уравнений динамики и кинематики ТИД, а также инерционностью позиционного контура управления ТИД составляет порядка 8 % – ошибки, остальные погрешности (2 % ошибки) являются незначительными и вызваны: неперпендикулярностью осей ТИД.
Максимальная приведенная погрешность воспроизведения составляет порядка: 2,5 % по тангажу (1,5`) и 1,5 % по рысканию (1,2`). Основными критериями, согласно которым режим начальной ориентации на Солнце считается выполненным, это достижение ориентации оси минус ОХ КА на Солнце в пределах ± 1,5°. Таким образом, точности воспроизведения вполне достаточно для проведения измерения выходных характеристик СОС.
Заключение
Приведенная методика расчета кинематических соотношений для формирования управляющего воздействия на рамки трехосного имитатора движения позволяет в связке с имитатором Солнца моделировать процесс углового отклонения позиционного прибора ориентации на Солнце относительно опорного ориентира. Учитывая конструктивные особенности ТИД (неограниченный поворот рамок), данная методика позволяет проводить всесторонние наземные испытания СОС, обеспечивает возможность организации режимов поиска ориентира по различным траекториям движения, что ранее осуществить не удавалось. Таким образом, наряду с обеспечением новых возможностей, данная методика позволяет повысить качество проведения полунатурных динамических испытаний систем ориентации и стабилизации. При этом приведенную методику возможно использовать для расчета управляющего воздействия на ТИД при моделировании процесса углового отклонения такого позиционного прибора, как: прибор ориентации на Землю (ПОЗ), заменив имитатор Солнца имитатором Земли.
Результаты моделирования показали, что предложенный подход с достаточной точностью воспроизводит имитацию углового движения, а погрешность, вносимая ТИД в процесс имитации, не оказывает влияния на процессы управления СОС в целом. Основная составляющая погрешности, вносимая лабораторный комплексом, это погрешность, вызванная несоостностью плоскопараллельного светового пучка имитатора Солнца с посадочным местом (центром план-шайбы ТИД) и точностью калибровочной выставки центра поля зрения испытуемого прибора с плоскопараллельным световым пучком имитатора Солнца. Остальные погрешности, такие как неперпендикулярность осей ТИД, не вносят существенных искажений в воспроизводимый процесс.
Полученные погрешности определяются расчетом и могут быть использованы в качестве поправок для уточнения результатов динамических испытаний СОС на комплексе моделирующих стендов, имеющем в своем составе ТИД. Такой подход позволит свести погрешность от экспериментального оборудования до величины погрешности прибора ориентации.
Рецензенты:
Пантелеев В.И., д.т.н., профессор, заведующий кафедрой электротехнических комплексов и систем, Сибирский федеральный университет, г. Красноярск;
Ловчиков А.Н., д.т.н., профессор, профессор кафедры систем автоматического управления, Сибирский государственный аэрокосмический университет имени академика М.Ф. Решетнева, г. Красноярск.



