В данной работе аналогично [1] проведен статистический анализ в пакете Statistica результатов оценивания знаний по высшей математике в объеме первых трех семестров 128-ми студентов 7-ми групп института электронного обучения Томского политехнического университета. Рассмотрение было проведено в системе 2-х показателей: ИДЗ – сумма баллов за выполнение 4-х индивидуальных домашних заданий в течение каждого семестра (по 60-ти балльной шкале); ЭКЗ – баллы, полученные в результате семестрового тест-экзамена (по 40-а балльной шкале). Гистограммная динамика положительных результатов ИДЭК (ИДЗk; ЭКЗk) по семестрам (k = 1, 2, 3) отражена на рис.1.
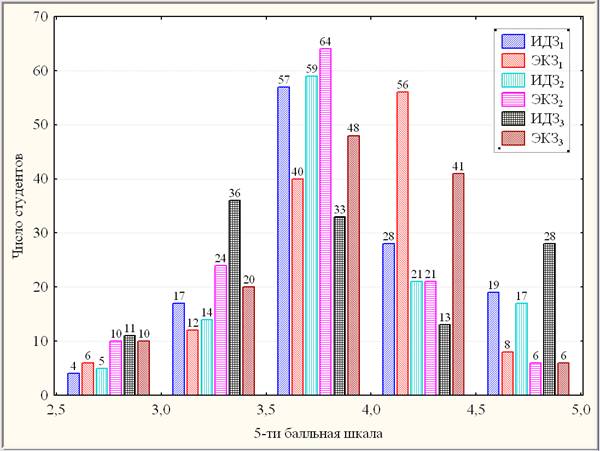
Рис. 1. Составная гистограмма ИДЭК (фрагмент положительных результатов)
Согласно рис.1, наиболее представительным является интервал слабых хорошистов [3,5; 4]. Здесь результаты текущей (ИДЗ) успеваемости стабильны на уровне 45–46 % в течение 1-го года обучения, но затем уменьшились почти в 2 раза (до 26 %) в 3-ем семестре. При этом результаты экзаменационной (ЭКЗ) успеваемости сначала выросли с 31 % в 1-ом семестре до 50 % во 2-ом семестре, а затем уменьшились до 38 % в 3-ем семестре. Заметим, что, если в 1-ом семестре динамика (сравнение ЭКЗ с ИДЗ) отрицательная, то в 3-ем семестре – положительная. В интервале сильных хорошистов [4; 4,5] продолжилась отрицательная динамика текущей успеваемости (уменьшение ИДЗ с 22 % в 1-ом семестре до 16 % во 2-ом семестре и 10 % в 3-ем семестре). При этом результаты экзаменационной успеваемости, наоборот, сначала уменьшились почти в 3 раза с 44 % в 1-ом семестре до 16 % во 2-ом семестре, а затем выросли до 32 % в 3-ем семестре. В интервале отличников [4,5; 5] наблюдается расслоение результатов текущей и экзаменационной успеваемости: если ЭКЗ стабильны на уровне 5–6 %, то ИДЗ, превышая ЭКЗ в »3 раза, демонстрируют положительную динамику роста с 13 % во 2-ом семестре до 22 % в 3-ем семестре.
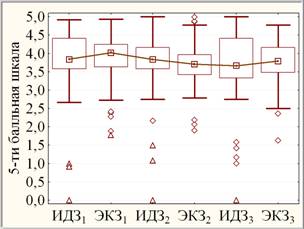
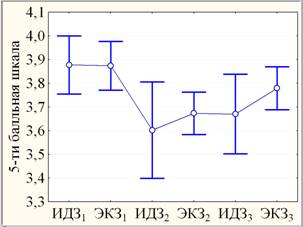
Согласно теории измерительных шкал балльная шкала измерения ИДЗ и ЭКЗ относится к типу порядковых шкал, позволяющих ранжировать (упорядочить) результаты оценивания качества усвоения знаний студентов. Поэтому для сравнения рассматриваемых выборок предлагается использовать прежде всего более корректные непараметрические характеристики (рис. 2, слева), а также привычные параметрические (рис. 2, справа).
|
|
|
Рис. 2. Медианные диаграммы размаха (слева: квадрат – медианы; ящик – квартильный размах; усы – полный размах без выбросов; ромб – выбросы, треугольник – крайние точки) и линейные графики средних (справа: круг – средние; усики – 95 % границы доверительных интервалов) ИДЭК
Согласно ранговому дисперсионному анализу Фридмана с повторными измерениями динамика ИДЭК (рис. 2, слева) оценивается как высоко значимая (на уровне значимости р < 0,0005) по совокупности трех семестров за счет отличия, например, ЭКЗ2 от ЭКЗ1 и ИДЗ1 – высоко значимо (р< 0,0005), от ИДЗ2 и ЭКЗ3 – статистически значимо (0,005<р< 0,050) при незначимом (р > 0,1) отличии от ИДЗ3.
По параметрическому дисперсионному анализу с повторными измерениями динамика ИДЭК (рис. 2, справа) оценивается как статистически значимая (0,005<р »0,007< 0,050) по совокупности трех семестров за счет отличия, например, ЭКЗ2 от ЭКЗ1 и ИДЗ1 – сильно значимо (0,0005< р < 0,005), от ЭКЗ3 – слабо значимо (0,05<р< 0,10) при незначимом (р > 0,1) отличии от ИДЗ2 и ИДЗ3.
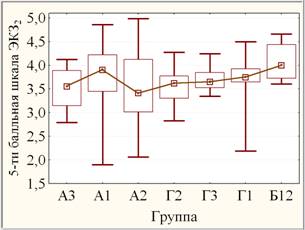
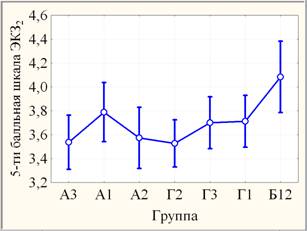
С другой стороны, в рамках однофакторного дисперсионного анализа независимых выборок с помощью непараметрического критерия Краскела – Уоллиса все выборки показателей текущей и экзаменационной успеваемости (ИДЗk; ЭКЗk, k = 1, 2, 3) оценены на однородность, то есть на различия между результатами 7-ми групп: слабо значимую в случае ИДЗ1, высоко значимую – ИДЗ2 и ИДЗ3, незначимую – ЭКЗ1 и ЭКЗ3, а в случае ЭКЗ2 как статистически значимую (на уровне 0,005 < р »0,018 < 0,050) за счет статистически значимых отличий Б12 от Г2 и А3 (рис. 3, слева). По параметрическому F-критерию различия 7-ми групп оцениваются как слабо значимые в случае ИДЗ1, высоко значимые – ИДЗ2 и ИДЗ3, незначимые – ЭКЗ1 и ЭКЗ3, а в случае ЭКЗ2 как слабо значимые (на уровне 0,050 < р »0,058 < 0,100) за счет слабо значимых отличий Б12 от остальных групп, кроме А1 (рис. 3, справа).
|
|
|
Рис. 3. Медианные диаграммы размаха (слева) и линейные графики средних (справа)
групп ЭКЗ2
Таким образом, результаты параметрического дисперсионного анализа в более мягкой форме полностью подтверждают результаты непараметрического (рангового) дисперсионного анализа как относительно динамики ИДЭК, так и однородности составных выборок (ИДЗk; ЭКЗk, k = 1, 2, 3). Составная динамика групповых средних ИДЭК представлена на рис. 4.
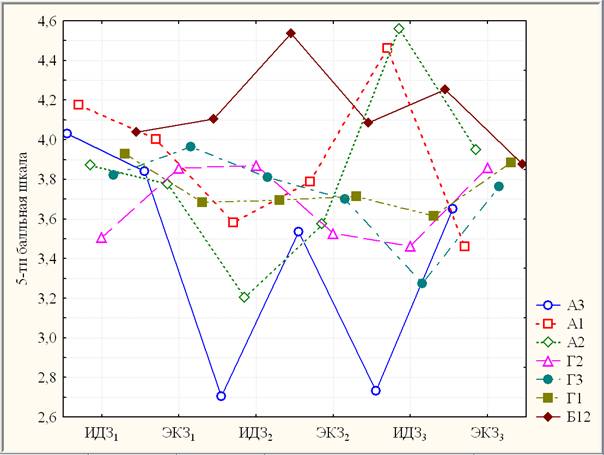
Рис. 4. Динамика групповых средних ИДЭК
На основании параметрического дисперсионного анализа повторных испытаний (рис. 4) можно заключить, что группа Г1 является единственной, имеющей стабильную (незначимую) динамику ИДЭК. Почти стабильную динамику имеют Б12 (только ИДЗ2 и ЭКЗ3 различаются статистически значимо на уровне значимости р » 0,02) и Г3 (ИДЗ3 отличается от всех остальных статистически значимо). Нестабильную статистически значимую динамику имеет Г2 (средние ЭКЗ1, ИДЗ2 и ЭКЗ3 отличаются статистически значимо от средних ИДЗ1, ЭКЗ2 и ИДЗ3). Остальные группы имеют более нестабильную динамику: А1 (ИДЗ3 отличается высоко значимо от ИДЗ2 и ЭКЗ3, сильно значимо от ЭКЗ2 и статистически значимо от ЭКЗ1; при этом статистически значимо различаются также ИДЗ1 и ИДЗ2, ЭКЗ1 и ЭКЗ3, а ИДЗ1 и ЭКЗ3 различаются сильно значимо), А2 (ИДЗ3 отличается высоко значимо от ИДЗ2 и ЭКЗ2, сильно значимо от ИДЗ1 и ЭКЗ1 и статистически значимо от ЭКЗ3; при этом ИДЗ2 отличается статистически значимо от ИДЗ1 и ЭКЗ1 и сильно значимо от ЭКЗ3), А3 (ИДЗ2 и ИДЗ3 отличаются высоко значимо от остальных; при этом статистически значимо различаются ИДЗ1 и ЭКЗ2).
Характерной чертой нестабильной высоко значимой динамики ИДЭК является наличие аномальных отклонений (особенно ИДЗ2 и ИДЗ3 (рис. 2) для группы А3 (рис. 4)). Данный результат свидетельствует о нарушении правил проведения тест-экзамена (без фактического допуска по результатам ИДЗ), что тем не менее практически не сказывается на стабильном уровне тест-экзаменационной динамики (рис. 4).
По-прежнему острой проблемой оценивания усвоенных студентом-заочником знаний в режиме ДОТ является чрезмерное увлечение автоматизацией (практически без участия преподавателя) итогового контроля знаний обучаемых в условиях несовершенства содержания и формы тестовых заданий, что приводит к завышению на целый балл (по 5-ти балльной шкале) результатов оценивания усвоенных студентом-заочником знаний в режиме ДОТ по сравнению с классическим режимом [1]. Можно заметить, что стадия оценивания усвоенных студентом знаний при дистанционном обучении с использованием информационных образовательных интернет-технологий порождает проблему идентификации личности в учебной on-line среде [1, 6, 10].
Результаты проведенного анализа оценивания знаний студентов-заочников в режиме ДОТ могут быть учтены при внедрении современных информационных образовательных интернет-технологий в организацию электронного и дистанционного обучения для обеспечения качества образования и контроля знаний.
Выводы
1. Проведена гистограммная динамика положительных результатов текущей (ИДЗ) и экзаменационной (ЭКЗ) успеваемости студентов электронного обучения по высшей математике в объеме первых трех семестров.
2. Согласно ранговому дисперсионному анализу Фридмана с повторными измерениями динамика ИДЭК оценивается как высоко значимая (р < 0,0005) по совокупности трех семестров за счет отличия, например, ЭКЗ2 от ЭКЗ1 и ИДЗ1 – высоко значимо (р < 0,0005), от ИДЗ2 и ЭКЗ3 – статистически значимо (0,005<р< 0,050) при незначимом (р > 0,1) отличии от ИДЗ3.
3. С помощью непараметрического критерия Краскела – Уоллиса все выборки показателей текущей и экзаменационной успеваемости оценены на однородность: слабо значимую в случае ИДЗ1, высоко значимую – ИДЗ2 и ИДЗ3, незначимую – ЭКЗ1 и ЭКЗ3, а в случае ЭКЗ2 как статистически значимую (на уровне р »0,018) за счет статистически значимых отличий группы Б12 от Г2 и А3.
4. Сделан вывод о том, что результаты параметрического дисперсионного анализа в более мягкой форме полностью подтверждают результаты непараметрического (рангового) дисперсионного анализа как относительно динамики ИДЭК, так и однородности составных выборок.
5.
На
основании параметрического дисперсионного анализа повторных испытаний проведены
оценки статистической значимости нестабильности динамики групповых средних ИДЭК.
Работа выполнена при поддержке Российского научного фонда.
Рецензенты:
Трифонов А.Ю., д.ф.-м.н., профессор кафедры высшей математики и математической физики, ФГБОУ ВПО «Национальный исследовательский Томский политехнический университет», г. Томск;
Арефьев К.П., д.ф.-м.н., профессор кафедры высшей математики, ФГБОУ ВПО «Национальный исследовательский Томский политехнический университет, г. Томск.