Существующие тенденции развития управляющих функций потоками трафика и унификации протоколов управления, реализованные в концепциях сетей следующего поколения NGN [1; 5],позволяют судить о том, что выбор метода определения маршрута между точкой входа и выхода трафика из сети для реализации управляющих функций должен быть централизованным и базироваться на алгоритмах, способных в реальном времени отслеживать состояние сети и принимать решение о маршрутах продвижения пакетов данных. В связи с чем разработка новых методов анализа и управления трафиком в сетях VPNявляется актуальной задачей.
Существующие методы анализа сетей VPN базируются либо на граф-комбинаторных алгоритмах [5], либо на математическом аппарате теории массового обслуживания или сетей Маркова [1]. В данной статье предложен другой подход к получению математической модели сети VPN на основе тензорного анализа [3], согласно которому сеть можно рассматривать как совокупность геометрических объектов в пространстве, размерность которого определяется топологией сети.Преимуществом данного подхода является простота алгоритма получения математической модели, описывающей состояние сети в виде системы линейных уравнений, решение которого в зависимости от накладываемых ограничений обеспечивает оптимальное распределение трафика между сайтами VPN-сети.
1. Постановка задачи
Исходными данными для анализа VPN-сети служит топология сети провайдера, предоставляющего услуги VPN, матрица запросов между отдельными сайтами VPN, потоки между сайтами VPN, как правило, задаются в виде матрицы запросов, представляющей собой матрицу размерности DxD, где элемент dij показывает интенсивность потока от i-го сайта до j-го сайта одной сети VPN.
Анализируемыми характеристиками являются потоки трафика и загрузка каналов связи при ограничениях на параметры качества обслуживания. В результате анализа будут предложены маршруты прохождения трафика между каждой парой сайтов.Пусть топология сети провайдера представлена в виде ориентированного графаG(N,A), где каждое ребро графа определяет однонаправленный канал связи. Как известно из теории массового обслуживания,в качестве математической моделиоднонаправленного двухточечного каналы связиможет выступать одноканальная система массового обслуживания, так как алгоритм обслуживания пакетов в интерфейсе маршрутизатора/коммутатора соответствует модели обслуживания одноканальной СМО. Таким образом,в качестве модели всей сети выступает сеть массового обслуживания.Граф сети массового обслуживания может быть описанматрицей инцидентности I, каждый элемент которой равен -1 или 1 и показывает: входит или выходит ветвь i из узла j. С целью удовлетворения условия сохранения потока необходимо все узлы, которые инцидентны только одной ветви, объединить в один узел, тем самым сеть преобразуется в контурную сеть [2]. В результате матрица инцидентности будет иметь на n-1 строку меньше, чем исходная, где n число объединяемых узлов, новая строка матрицы инцидентности будет равна сумме строк объединяемых узлов.
2. Общий подход к решению задачи тензорным методом
Основной идеей тензорного метода является то, что все топологии, содержащие одинаковое число ветвей, связаны между собой тензором преобразования, в роли которого могут выступать матрица линейнонезависимых разрезов, или матрица линейнонезависимых контуров, или объединенная матрица линейнонезависимых контуров и разрезов.
Поскольку все сети с топологией, состоящей из одинакового числа ветвей, связаны между собой тензором преобразования, то среди множества проекций можно выделить так называемую примитивную сеть [3].Примитивная сеть состоит из такого же количества ветвей, как и исследуемая сеть, но количество несвязанных компонент в ней также равно числу ветвей, в связи с чем потоки в каждой ветви примитивной сети оказываются независимыми. Топология примитивной контурной сети показана на рисунке 1. Как видно, в примитивной контурной сети каждой контурной интенсивности соответствует интенсивность в соответствующей ветви.

Рис.1. Примитивная контурная сеть
Если определить математическую модель простейшего элемента
сети, которым является одноканальная СМО, как ![]() ,
то согласно постулату обобщения Крона математическая модель примитивной сети
имеет тривиальный вид и показывает связь контурных интенсивностей с контурными
временами обслуживания и контурными загрузками
,
то согласно постулату обобщения Крона математическая модель примитивной сети
имеет тривиальный вид и показывает связь контурных интенсивностей с контурными
временами обслуживания и контурными загрузками![]() или
в матричной форме:
или
в матричной форме:
 (1)
(1)
где: λi(i=1…n) – интенсивность поступления, поступающая на вход, элемента сети;ti (i=1…n) – среднее время обслуживания;ρi (i=1…n) – загрузка i-го элемента.
Если в качестве базисных элементов для каждой топологии будут
использоваться линейнонезависимые контуры, то тензор преобразования
устанавливает связь между контурными интенсивностями одной сети с контурными
интенсивностями другой сети. Так, связь контурных интенсивностей примитивной
сети связана с контурными интенсивностями исследуемой сети тензором
преобразования С: ![]() .
.
Количество контурных интенсивностей анализируемой сети
определяется цикломатическим числом, равным:![]() .
.
Тензор преобразования С определяется как матрица линейнонезависимых контуров. Есть различные методы получения матрицы контуров: граф-комбинаторные и аналитический.Граф-комбинаторные методы основаны на таких алгоритмах, как поиск в глубину и поиск в ширину.Следует отметить, что сложность таких алгоритмов равна O(N), то есть растет линейно с увеличением числа ветвей сети. Аналитический способ предполагает нахождение матрицы контуров как матрицу, ортогональную матрице инцидентности, так как матрица инцидентности является также одной из множеств матриц разрезов, но с одной линейнозависимой строкой. Иными словами, произведение матрицы инцидентности без одной произвольной строки на матрицу линейнонезависимых контуров дает матрицу с нулевыми элементами.Используя это правило,можно найти матрицу линейно независимых контуров.
В общем случае значение элементов матрицы контуров не имеет значения, главное, чтобы контуры, находящиеся в каждом столбце, были линейно независимыми.Но для расчетов удобным оказывается использование матрицы не просто с линейнонезависимыми контурами, а с фундаментальными циклами, именно такая матрица и выбрана в качестве тензора преобразования.
Именно матрицы фундаментальных циклов, в отличие от просто матриц линейнонезависимых контуров, явным образом показывают, что если заданы потоки в контурах примитивной сети, номера которых соответствуют номерам строк, в которых все элементы кроме одного равны нулю, то после преобразования примитивной сети в исследуемую потоки в оставшихся ветвях будут однозначно определены как линейная комбинация заданных потоков. Если же выбрать произвольную матрицу линейнонезависимых контуров, то такая связь будет неочевидной.
Связь контурных интенсивностей примитивной сети с исследуемой можно, как уже было сказано, записать следующим образом:
![]() , (2)
, (2)
где ![]() –контурные
интенсивности примитивной сети;
–контурные
интенсивности примитивной сети; ![]() – тензор преобразования контурных
интенсивностей исследуемой сети в контурные интенсивности примитивной сети;
– тензор преобразования контурных
интенсивностей исследуемой сети в контурные интенсивности примитивной сети; ![]() – значение контурных интенсивностей
исследуемой сети.
– значение контурных интенсивностей
исследуемой сети.
С помощью несложных матричных преобразований можно показать,
что вектор контурных загрузок исследуемой сети может быть записан, как:![]() , и матрица контурных длительностей
обслуживания исследуемой сети определена в виде:
, и матрица контурных длительностей
обслуживания исследуемой сети определена в виде:
![]() (3)
(3)
где С' – тензор преобразования без линейнозависимых строк.
На основании полученных значений контурных загрузок и контурных времен обслуживания значения контурных интенсивностей исследуемой сети можно записать, как:
![]() . (4)
. (4)
А значение потоков в каждой ветви можно определить следующим образом:
![]() .
(5)
.
(5)
Поскольку для каждой сети VPN известны свои матрицы запросов, проводя тензорный анализ характеристик для каждой VPN-сети по отдельности, тем самым получив столько систем уравнений типа (4), сколько существует сетей VPN, затем просуммировав одноименные строки всех уравнений, получаем финальную систему уравнений, отражающую зависимость интенсивностей потоков в каждом канале связи от загрузок создаваемой каждой отдельной сетью VPN. Таким образом, если число сетей VPN равно N, то окончательная система уравнений, определяющая потоки всех VPN-сетей в каждой ветви исследуемой сети, будет следующей:
![]() , (6)
, (6)
где ![]() - матрица контурных интенсивностей,
создаваемая p-м
сайтом q-й VPN-сети.
- матрица контурных интенсивностей,
создаваемая p-м
сайтом q-й VPN-сети.
Система уравнений (6) содержит n уравнений, где n- число ветвей в
анализируемой сети, а число неизвестных равно ![]() ,
где S- общее число
сайтов всех VPN-сетей. Следовательно, система уравнений
(6) имеет бесконечное число решений. Это связано с тем, что каждое решение
системы уравнений определяет какой-либо маршрут прохождения трафика между
сайтами VPN-сетей, а поскольку вариантов прохождения
маршрутов существует бесконечное множество, то и система уравнений имеет
бесконечное число решений. Систему уравнений (6) можно использовать для анализа
трафика VPN двумя способами. Первый вариант вытекает из
того, что в системе (6) потоки в каждой ветви выражаются через
линейнонезависимые загрузки, поэтому определив потоки/загрузки только в линейно
независимых ветвях, автоматически определяются и потоки/загрузки в оставшихся
ветвях. Второй вариант использования системы уравнений (6) заключается в
отыскании какого-либо решения, а не в подборе значений линейнонезависимых
компонент, при этом полученное решение будет описывать маршруты между сайтами VPN, но при таком подходе система уравнений (6) должна
решаться с рядом обязательных ограничений в виде системы неравенств. Обязательными
ограничениями для сиcтемы уравнений (6) являются:неотрицательность
потоков создаваемой отдельным сайтом q-й VPN-сети, значение суммарного
потока в канале связи не должно превышать величину пропускной способности
данного канала, величина потока в ветви nот p-го
сайтаq-й VPN не должна превышать величину потока, создаваемую p-м сайтом q-ой VPN сети, а
также необходимо обеспечить отсутствие появления петлевых маршрутов.Дополнительными
ограничениями, накладываемыми на систему уравнений (5), могут быть ограничения
сквозной задержки или вероятности потерь каждого типа трафика, создаваемого
сайтами VPN-сетей.
,
где S- общее число
сайтов всех VPN-сетей. Следовательно, система уравнений
(6) имеет бесконечное число решений. Это связано с тем, что каждое решение
системы уравнений определяет какой-либо маршрут прохождения трафика между
сайтами VPN-сетей, а поскольку вариантов прохождения
маршрутов существует бесконечное множество, то и система уравнений имеет
бесконечное число решений. Систему уравнений (6) можно использовать для анализа
трафика VPN двумя способами. Первый вариант вытекает из
того, что в системе (6) потоки в каждой ветви выражаются через
линейнонезависимые загрузки, поэтому определив потоки/загрузки только в линейно
независимых ветвях, автоматически определяются и потоки/загрузки в оставшихся
ветвях. Второй вариант использования системы уравнений (6) заключается в
отыскании какого-либо решения, а не в подборе значений линейнонезависимых
компонент, при этом полученное решение будет описывать маршруты между сайтами VPN, но при таком подходе система уравнений (6) должна
решаться с рядом обязательных ограничений в виде системы неравенств. Обязательными
ограничениями для сиcтемы уравнений (6) являются:неотрицательность
потоков создаваемой отдельным сайтом q-й VPN-сети, значение суммарного
потока в канале связи не должно превышать величину пропускной способности
данного канала, величина потока в ветви nот p-го
сайтаq-й VPN не должна превышать величину потока, создаваемую p-м сайтом q-ой VPN сети, а
также необходимо обеспечить отсутствие появления петлевых маршрутов.Дополнительными
ограничениями, накладываемыми на систему уравнений (5), могут быть ограничения
сквозной задержки или вероятности потерь каждого типа трафика, создаваемого
сайтами VPN-сетей.
Таким образом, решая систему уравнений (6) с учетом неотрицательности потоков или другими ограничениями, накладываемыми на качество обслуживания потоков сетей VPN, а также учитывая значения матриц запросов, можно однозначно определять маршруты прохождения трафика между сайтами VPN-сетей. В свою очередь если решение системы уравнений (6) совместно с накладываемыми ограничениями найти не удается, то это означает, что данная сеть не может передать то количество трафика, которое генерируется каждой VPN-сетью с требуемым качеством обслуживания.
3. Численные результаты
В качестве примера проведем анализ сети VPN,приведённой на рисунке 2.
На рисунке 2под условным обозначением УК показаны узлы коммутации, в роли которых, как правило, выступают маршрутизаторы или коммутаторы.
Согласно [4],математическая модель исследуемой сети может быть представлена в виде сети массового обслуживания (рисунок 3).
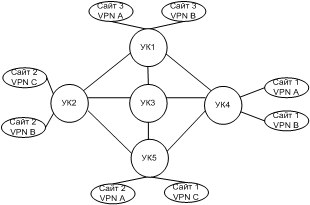
Рис.2. Пример организации сети VPN
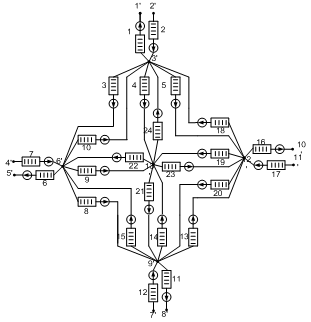
Рис.3. Сеть массового обслуживания для исследуемой сети
В соответствии с контурным методом анализа узлы 1’, 2’, 4’, 5’, 7’, 8’,10’, 11’объединяются в один узел, после определяется тензор преобразования от структуры исследуемой сети к структуре примитивной сети, который связывает контурные интенсивности исследуемой сети с контурными интенсивностями примитивной. Затем по формулам (2)-(3) определяются контурные загрузки и контурные времена обслуживания. После чего определяются контурные интенсивности анализируемой сети по формуле (4), затем по формуле (5) определяются потоки в каждой ветви, создаваемыеp-мсайтом q-йVPN, затем по формуле (6) определяются потоки в каждой ветви, создаваемые всеми сайтами.
В качестве исходных данных определены матрицы запросов сайтов
VPN![]()
![]()
![]() в виде:
в виде: 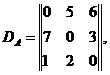
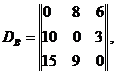
![]() Элементы матриц показывают, сколько
единиц информации в секунду предается от i-го сайта к j-му
в рамках одной VPN.Так, элемент матрицы DA, находящийся в первой строке и втором столбце,
показывает, что из первого сайта во второй сайт VPN А
будет передаваться 5 ед. инф./с. Время обслуживания одной единицы информации
приято как 0,01 с, что подразумевает скорость 100 единиц в секунду. При таких исходных
данных одним из решений системы уравнений (6) соответствует следующее
распределение:
Элементы матриц показывают, сколько
единиц информации в секунду предается от i-го сайта к j-му
в рамках одной VPN.Так, элемент матрицы DA, находящийся в первой строке и втором столбце,
показывает, что из первого сайта во второй сайт VPN А
будет передаваться 5 ед. инф./с. Время обслуживания одной единицы информации
приято как 0,01 с, что подразумевает скорость 100 единиц в секунду. При таких исходных
данных одним из решений системы уравнений (6) соответствует следующее
распределение:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Каждый вектор показывает, какая интенсивность в ветвях создается p-м сайтом VPN_q. Суммарный вектор интенсивностей для каждой ветви представлен в таблице 1.
Таблица 1
|
Номер ветви |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Интенсивность поступления |
18 |
27 |
15 |
2 |
10 |
32 |
23 |
10 |
10 |
3 |
17 |
19 |
|
Номер ветви |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Интенсивность поступления |
7 |
3 |
9 |
27 |
25 |
12 |
8 |
5 |
2 |
8 |
10 |
3 |
Также при решении данной задачи в качестве ограничений
выступало то, что значения элементов векторов![]() и
и
![]() должны находиться в диапазоне [0;100).
Таким образом, полученное решение удовлетворяет поставленным ограничениям, при
этом необходимо отметить, что это одно возможное из множества решений.
должны находиться в диапазоне [0;100).
Таким образом, полученное решение удовлетворяет поставленным ограничениям, при
этом необходимо отметить, что это одно возможное из множества решений.
Заключение
В данной статье представлен метод исследования сетей VPNcиспользованием контурного метода анализа. В связи с тем что сетевая структура многих организаций строится именно на базе сетей VPN, провайдеры, предоставляющие данный вид услуг, должны обеспечиватьгарантии по качеству обслуживания потоков трафика для каждой VPN. Большое количество поддерживаемых сайтов VPNи разветвленная инфраструктура сети провайдера делает задачу управления потоками трафика достаточно рутинной, в свою очередь предложенный метод анализа очень хорошо описывает распределения трафика в больших системах благодаря хорошо формализованному матричному математическому аппарату, который остается инвариантным к размеру исследуемой топологии. Также необходимо отметить, что арифметические операции, производимые над матрицами, являются хорошо распараллеливаемыми вычислительными операциями, что позволит на многопроцессорных системах сократить время анализа сетей VPN. Преимуществами данного подхода по сравнению с существующими методами является простота получения математической модели, сложность вычисления маршрутов между сайтами VPNрастет линейно с увеличением числа каналовв сети провайдера,в случае если необходимо провести анализ возможности организации маршрута по конкретным ветвям сети.Но если стоит задача в поиске произвольного маршрута, который будет являться решением системы уравнения (6), то накладываемое ограничение на отсутствие маршрутных петель в каждом маршруте между сайтами VPNувеличивает сложность задачи. Также необходимо отметить, что вид тензора преобразования контурных интенсивностей полностью определяется матрицей линейнонезависимых циклов исследуемой сети, поэтому в результате исследований сетей VPNс различной структурой контурным методом можно сформулировать несколько требований к выбору матрицы линейнонезависимых циклов, с целью уменьшения временных затрат на вычисление. В качестве тензора преобразования лучше выбирать матрицу фундаментальных циклов или матрицу линейнонезависимых циклов, где каждый цикл включаетв себя ветвь источника и ветвь получателя, данные утверждения носят исключительно эмпирический характер и требуют дополнительных исследований, выявляющих зависимости алгоритмической сложности от вида матрицы линейнонезависимых контуров.
Рецензенты:Петров М.Н., д.т.н., проф., ФГБОУ ВПО «СибГАУ», г. Красноярск.
Антамошкин А.Н., д.т.н., проф., профессор каф. САиИОФГБОУ ВПО «Сибирский государственный аэрокосмический университет им. акад. М.Ф. Решетнева», г. Красноярск.



