Scientific journal

Modern problems of science and education

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

Весь строительный процесс представляет собой постоянно изменяющуюся во времени сложную параметрическую систему. Параметры строительного процесса, например, количество рабочих на строительной площадке, объем выполняемых работ, постоянно изменяют свои значения, создавая определенные колебания и отклонение значений параметров от определенной средней величины. Все изменения значений параметров можно представить в виде ряда данных.

Согласно изложенной гипотезе Ж. Б. Ж. Фурье, не существует функции, которую нельзя было бы разложить в тригонометрический ряд. Любой сигнал, представленный рядом данных, можно разложить на различные синусоидальные составляющие с различными частотами, вследствие чего можно определить, как возник первоначальный сигнал, по какому пути он следовал или, наконец, какому внешнему влиянию он подвергался. Таким образом, можно получить информацию для выяснения происхождения сигнала. Подобный метод анализа называется спектральным анализом или анализом Фурье [1, 2, 3, 4, 5,6].

Цель работы: применение метода спектрального анализа для выявления изменений функции выполненных объемов работ и дальнейшей оптимизации календарного плана.

Рассмотрим дискретное преобразование Фурье (далее – ДПФ) и быстрое преобразование Фурье (далее – БПФ).Для реализации ДПФ необходимо конечное число входных данных N. Уравнение для получения N-точечного ДПФ имеет следующий вид [3]:

        (1)

Также существует обратное дискретное преобразование Фурье (далее – ОДПФ), которое определяется как:

,             (2)

где N – количество значений сигнала за период, т.е. количество компонент разложения;

x(n) – значения сигнала (в дискретных временных точках с номерами n=0,…, N-1), которые являются входными данными для прямого преобразования и выходными для обратного;

X(k) – спектр исходного сигнала, состоящий из N комплексных амплитуд синусоидальных сигналов, в совокупности представляющих собой исходный сигнал, частотный выход ДПФ в k-той точке спектра, где k находится в диапазоне от 0 до N-1, что является выходными данными для прямого преобразования и входными для обратного.

Физический смысл дискретного преобразования Фурье состоит в том, чтобы представить некоторый дискретный сигнал в виде суммы гармоник. Параметры каждой гармоники вычисляются прямым преобразованием, а сумма гармоник – обратным [7]. Набор гармоник, выделенных в сигнале – это и есть спектр. Каждая гармоника характеризуется тремя параметрами: амплитудой, частотой и фазой.

БПФ по сути является алгоритмом для ДПФ для упрощения и сокращения количества вычислений, которые необходимо проделать при ДПФ. В БПФ число вводимых данных сигнала ограничивается условием:

N = 2k,                                                             (3)

где k – значение степени.Таким образом, в системе БПФ можно обрабатывать сигналы с количеством данных 2, 4, 8, 16, 32, 64, 128 и т.д. [8]

Используем БПФ для анализа данных о ежедневных средних объемах работ, выполняемых при строительстве типового монолитного жилого дома. Исходными данными являются сведения о средних объемах забетонированных конструкций в день за 4,5 месяца работы бригады (таблица 1). Пусть x (n) –  значение выполненного объема работ в n-ый день работы бригады, где n=0,…, N-1. Количество значений в ряде данных принимаем N=128, что, в свою очередь, удовлетворяет условию (3) для БПФ. В ряд данных не вошли нулевые значения объемов работ, относящиеся к предпраздничным и праздничным дням (конец декабря, начало января).В программе TableCurve 2D v5.01 с помощью аппарата БПФ (FFT – FastFouriertransform) разложим исходный сигнал, представленный рядом данных таблицы 1, в ряд Фурье. В результате разложения сигнал делится на постоянную составляющую и 32 гармонических колебания или просто 32 гармоники. Каждая гармоника характеризуется своим периодом, частотой и амплитудой.Функция, получаемая в результате сложения нескольких гармоник, называется приближающей функций, а сама операция – приближением. Таким образом, сложив постоянную составляющую и первую гармонику, получили первое приближение, а сложив 10 первых гармоник и постоянную составляющую, получили десятое приближение и т. д. Суммируя все гармоники, получили саму функцию во временной области и частотную область (рисунки 1, 2). Значения частот от низких до высоких расположены по оси абсцисс. По оси ординат могут быть расположены значения амплитуд гармоник, значения фаз, магнитуд или мощностей сигнала.

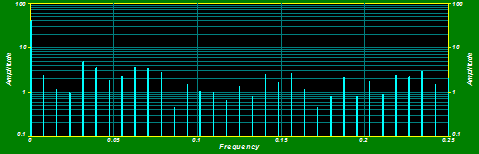
Рис. 1. Частотная область сигнала

Таблица 1

Исходные данные

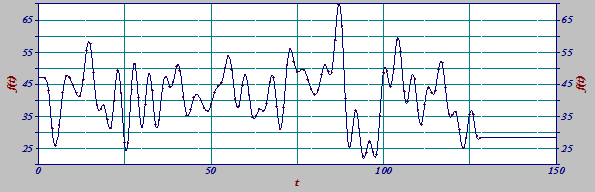
Рис. 2. Временная область сигнала

В таблице 2 представлены вычисленные коэффициенты Фурье для 32 гармоник.

Таблица 2

Коэффициенты Фурье

 

Исследование поведения функции изменения ежедневных средних объемов работ с помощью различных приближений, при каждом последующем приближении наглядно показывает малейшие изменения функции и позволяет определить, на каком участке функции и в какой момент времени такое изменение произошло. Все изменения, происходящие с функцией легко сопоставить с рабочим процессом, т. к. значения функции можно определить в каждой точке периода (в нашем случае это 4,5 месяца) как для любого приближения, так и для итоговой функции. Рассмотрим 10-е приближение функции и выделим зоны максимальных отклонений (рис. 3).

 

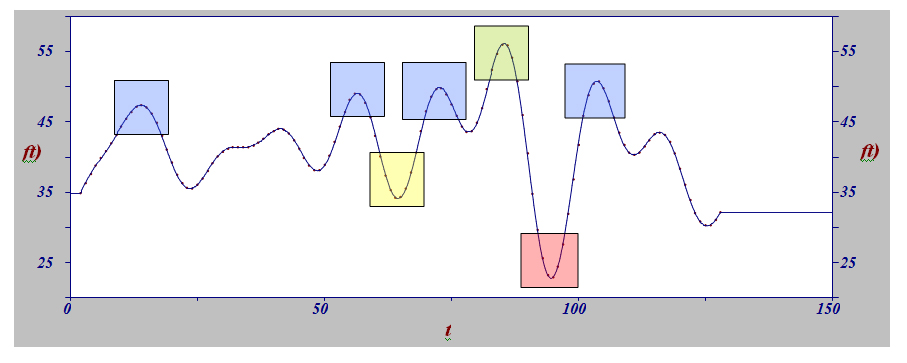
Рис. 3. Поведение функции при десятом приближении

На основании собранных за исследуемый период времени статистических данных о погодных условиях на строительной площадке, работе строительной техники (поломке/плановой настройке), задержке в поставках строительных материалов, о графике движения рабочих, построенном на основании табелей учета рабочего времени, можно проанализировать причины отклонений значений выполненных объемов работ. Минимальные значения среднего объема работ (красная зона) приходятся на начало января с 5-го по 14-й день. В данный промежуток времени имели место задержки в поставках бетона, неблагоприятные погодные условия. Количество рабочих было оптимальным, однако, выработка после праздничных дней оказалась очень низкой. Меньшее падение значений среднего объема работ относится к началу декабря с 1-го по 8-й день (желтая зона). В этот период времени происходило обесточивание строительной площадки дважды, продолжительностью отсутствия электроэнергии в течение 1-го часа. Также произошла поломка крана, который не работал в течение суток. Максимальное увеличение среднего объема работ (зеленая зона) приходится на конец декабря. В данный период времени работало максимальное количество рабочих с максимальной выработкой. Это связано с необходимостью завершения и сдачи определенного объема работ в конце периода. Другие пики увеличения среднего объема выполняемых работ (синяя зона) приходились на 7-17 октября, 23-29 ноября, 10-16 декабря, 16-22 января. В эти периоды наблюдалось увеличение количества рабочих.

Каждое последующее приближение дает возможность изучить поведение функции более детально и разбить ранее рассмотренные зоны на более мелкие, включающие в себя период времени от 3-х до 5-ти дней. На рисунке 4 показано семнадцатое приближение исследуемой функции, где ранее рассмотренную красную зону можно детализировать, разбив, например, на две подзоны. и проанализировать факторы, влияющие на изменение среднего объема работ в каждой подзоне. Аналогично желтую зону можно разбить на три подзоны. Увеличивая или уменьшая количество приближений, можно задать различную степень детализации функции: для обобщенного анализа, например, за период времени равный неделе, и для частного анализа, например, за период времени от трех до пяти дней.

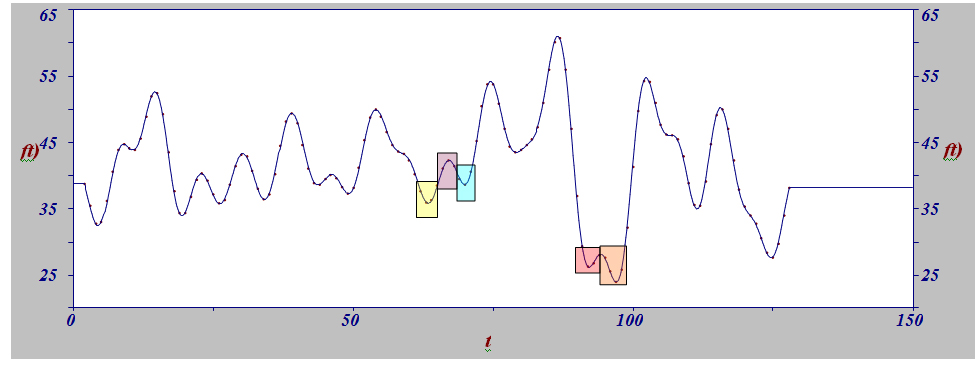
Рис. 4. Поведение функции при десятом приближении

Выводы:

1.    В работе проведенспектральный анализ изменений значений средних объемов работ за 4,5 месяца.

2.    Спектральный анализ позволяет рассмотреть поведение функции изменения средних объемов работ в нескольких вариантах: укрупненный анализ, для отображения общих зависимостей и причин изменения средних объемов работ, и детальный анализ, позволяющий определить точные факторы, влияющие на изменения значений за определенный узкий промежуток времени.

3.    Спектральный анализ позволит прогнозировать дальнейшее поведения функции изменения средних объемов работ в зависимости от факторов, влияющих на нее, а также корректировать календарный план работ, регулируя внешние и внутренние факторы, влияющие на ход строительного процесса.

Рецензенты:

Барабанщиков Ю.Г., д.т.н., профессор кафедры строительства уникальных зданий и сооружений Санкт-Петербургского политехнического университета Петра Великого, г.Санкт-Петербург;

Величкин В.З., д.т.н., профессор кафедры строительства уникальных зданий и сооружений Санкт-Петербургского политехнического университета Петра Великого,г.Санкт-Петербург.