Для производства сухого пиломатериала традиционно применяют конвективный способ сушки. Данный способ характеризуется хорошим качеством и обеспечивает бездефектную сушку с полным сохранением всех физико-механических свойств [5].
В современных условиях производства немаловажную роль играет снижение продолжительности сушки. При этом конвективная сушка твердолиственных пиломатериалов имеет значительные показатели по времени нахождения материала в сушильной камере [1;5].
В связи с этим находят применение новые способы сушки. Таким способом является вакуум-импульсная сушка.
Для определения механизма действия и расчёта продолжительности сушки был проведен сравнительный анализ сушки вакуум-импульсным и конвективным способом дубовых пиломатериалов.
Методы и результаты исследования
Для примера сравним процесс сушки дубового пиломатериала при предложенной вакуум-импульсной сушке – С1 и конвективной сушке – С2. В качестве объекта сушки возьмем образец дуба Д1 размерами 94х82х20 мм, начальная масса 118,41 г, влажность ![]() 38%, температура t0= 20 °С.
38%, температура t0= 20 °С.
Процесс сушки начинается с процесса прогревания, который протекает совершенно одинаково, как при конвективной сушке, так и при вакуум-импульсной.
Определим время прогревания образцов Д1.
Дубовая пластина, размером в поперечном сечении 20х82 мм (0,02х0,082 м), имеющая влажность 38 % и начальную температуру t0= 20 °С, нагревается в воздухе, температура которого 70 °С. Необходимо определить продолжительность нагревания, необходимую для получения в центре пластины температуру 60 ° С [4].
Находим приведенную величину определяющего размера по формуле
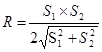 ,
,
где S1=0,02 м; S2= 0,082 м.
Имеем
![]()
Безразмерная координата точки
![]()
т.к. ![]() ; и S=0,01 м.
; и S=0,01 м.
Безразмерная температура ![]() равна
равна
![]()
По номограмме, построенной А.В. Лыковым в координатах х/R, находим критерий Фурье Fo=0,82 [1].
Коэффициент температуропроводности а равен
![]()
где С – удельная теплоемкость;
![]() – фактическая плотность древесины дуба при влажности 38 %;
– фактическая плотность древесины дуба при влажности 38 %;
![]() – коэффициент теплопроводности.
– коэффициент теплопроводности.
Древесина дуба имеет среднюю базисную плотность ![]() = 560 кг/м3 . Ее фактическая плотность при влажности 38 % (диаграмма плотности древесины) равна 750 кг/м3 [4].
= 560 кг/м3 . Ее фактическая плотность при влажности 38 % (диаграмма плотности древесины) равна 750 кг/м3 [4].
Для определения удельной теплоемкости С и коэффициента теплопроводности нужно знать, кроме влажности, температуру материала, которая в процессе нагревания непостоянна. В качестве температуры возьмем среднюю расчетную, °С:
tp= (t0+tс)/2 = (70+20)/ 2 = 45° С.
Удельная теплоемкость древесины дуба при этой температуре и влажности 38 % составляет С = 2,64 кДж/ (кг ∙° С). Коэффициент теплопроводности находим по (рис. 5, а) и формуле
![]()
Номинальное значение коэффициента теплопроводности находим по диаграмме К.Р. Кантера![]() Вт/(м∙0С). Искомый коэффициент теплопроводности определим по формуле
Вт/(м∙0С). Искомый коэффициент теплопроводности определим по формуле
![]() .
.
Полагаем Кх = 1,07
Величину Кр = 1,38 находим из табл.1 [4].
Таблица 1
Значения коэффициента Кр в зависимости от базисной плотности
|
кг/ м3 |
360 |
400 |
450 |
500 |
550 |
600 |
650 |
|
Кр |
1,00 |
1,05 |
1,12 |
1,22 |
1,36 |
1,56 |
1,86 |
Тогда величина коэффициента температуропроводности равна
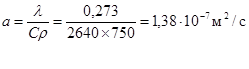
Искомая продолжительность нагревания составит
![]()
или ![]() 10 мин.
10 мин.
Прогрев древесину в течение 10 минут, приступаем к ее вакуум-импульсной сушке. Результаты сушки отражены в таблице 2.
Таблица 2
Результаты сушки дубовых образцов
|
1. |
Порода |
Дуб 1 |
Дуб 2 |
Дуб 3 |
Дуб 4 |
Дуб 5 |
Дуб 6 |
Дуб 7 |
|
2. |
Начальная масса (г) |
90,39 |
135,95 |
141,84 |
140,28 |
136,235 |
136,235 |
134,7 |
|
3. |
Начальная влажность (%) |
27 |
28 |
30 |
29 |
27 |
27 |
29 |
|
4 |
Давление разряжения, ат |
0,3 |
0,5 |
0,5 |
0,5 |
0,5 |
0,5 |
0,5 |
|
5 |
Время цикла, мин |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
|
6 |
Температура в камере, °С |
60 |
80 |
75 |
75 |
75 |
75 |
75 |
|
7 |
Время сушки, час |
11 |
7 |
8 |
8 |
7 |
8 |
8 |
|
8. |
Конечная влажность, % |
8-10 |
8-10 |
8-10 |
9-10 |
8-10 |
8 |
8 |
|
9 |
Конечная масса, г |
77,48 |
116,545 |
122,96 |
118,98 |
113,755 |
115,775 |
112,035 |
Рассмотрим теперь, какое время необходимо затратить, чтобы высушить образец Дуб 1 из таб.1 при конвективной сушке дубового образца размером в поперечном сечении 20x82 мм (0,02 x0,082 м), имеющего влажность 27 % в воздухе, движущемся со скоростью 2,0 м/с, при температуре t0 =60°С и ![]() = 0,3 до влажности 8 % [6].
= 0,3 до влажности 8 % [6].
Найдем коэффициент влагопроводностиа' для образца Дуб 1. Базисная плотность дуба равна ![]() = 560 кг!м3 . По левой половине диаграммы (см. рис. 1).
= 560 кг!м3 . По левой половине диаграммы (см. рис. 1).
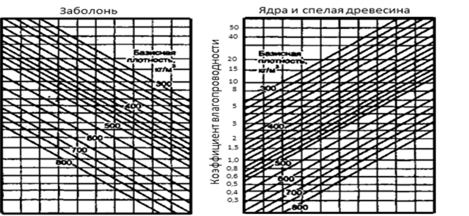
Рис. 1. Диаграмма коэффициента влагопроводности древесины в тангенциальном направлении
устанавливаем, что при температуре 60 °С и базисной плотности ![]()
коэффициент влагопроводности равен
а' = 4∙10-6 см2 / с.
Коэффициент влагообмена a' = 22∙10-5 см/с.
Приведенная толщина S определена равенством (1) и равна
![]()
По рисунку 2.4 в учебнике автора Расева А.И. [2;6] равновесная влажность древесины в воздухе данного состояния Wp =5,4 % . Величину ![]() считаем равной
считаем равной
![]() 0,81.
0,81.
Для определения времени сушки от начальной влажности Wн= 27 % до влажности Wк= 8 %, воспользуемся формулой
![]()
Подставляя имеющиеся значения для первого образца Дуб 1 получим
![]()
Получили, что при конвективной сушке первого образца Дуб 1 время сушки в 17 раз больше, чем при вакуум-импульсной сушке.
Рассмотрим теперь, какое время необходимо затратить, чтобы высушить образец Дуб 2 из таб. 1 при конвективной сушке дубового образца размером в поперечном сечении 20х82 мм (0,02x0,082 м), имеющего влажность 28 % в воздухе, движущемся со скоростью 2,0 м/с, при температуре t0=80 °С и ![]() = 0,3 до влажности 8 % [2].
= 0,3 до влажности 8 % [2].
Найдем коэффициент влагопроводности а' для образца Дуб 2. Базисная плотность дуба равна ![]() = 560 кг!м3. По левой половине диаграммы (см. рис. 1) устанавливаем, что при температуре 75 °С и базисной плотности
= 560 кг!м3. По левой половине диаграммы (см. рис. 1) устанавливаем, что при температуре 75 °С и базисной плотности ![]() =560 кг/м3 коэффициент влагопроводности равен
=560 кг/м3 коэффициент влагопроводности равен
а'= 8∙10-6 см2 /с.
Коэффициент влагообмена а' = 22 ∙10-5 см / с.
Приведенная толщина S определена равенством (1) и равна
S = 2 см .
Равновесная влажность древесины в воздухе данного состояния Wp=4,6 %[2;4].
Величину B считаем равной
В≈0,81.
Для определения времени сушки от начальной влажности Wн= 28 % до влажности Wк= 8 % воспользуемся формулой
![]()
Подставляя имеющиеся значения для второго образца Дуб 2, получим
![]()
Получили, что при конвективной сушке второго образца Дуб 2 время сушки в 3,5 раза больше, чем при вакуум-импульсной сушке.
Рассмотрим теперь, какое время необходимо затратить, чтобы высушить образец Дуб 3 из таб.1 при конвективной сушке дубового образца размером в поперечном сечении 20x82 мм( 0,02x0,082), имеющего влажность 30 % в воздухе, движущемся со скоростью 2,0 м/с, при температуре t0=75°Cи ![]() =0,3 до влажности 8 % [2].
=0,3 до влажности 8 % [2].
Найдем коэффициент влагопроводности а' для образца Дуб 3. Базисная плотность дуба равна ![]() =560 г/м3. По левой половине диаграммы (см. рис. 1) устанавливаем, что при температуре 75 °С и базисной плотности
=560 г/м3. По левой половине диаграммы (см. рис. 1) устанавливаем, что при температуре 75 °С и базисной плотности ![]() =560 г/м3 коэффициент влагопроводности равен
=560 г/м3 коэффициент влагопроводности равен
а' = 6,2∙10-6 см2/с.
Приведенная толщина S определена равенством (1) и равна
S= 2 см.
Равновесная влажность древесины в воздухе данного состояния Wp=5,3 % [4;6]. Величину В считаем равной
В≈0,81
Для определения времени сушки от начальной влажности Wн=30 % до влажности Wк= 8 % воспользуемся формулой
![]()
Подставляя имеющиеся значения для второго образца Дуб 3, получим
![]()
Получили, что при конвективной сушке третьего образца Дуб 3 время сушки в 4,5 раза больше, чем при вакуум-импульсной сушке.
Рассмотрим теперь, какое время необходимо затратить, чтобы высушить образец Дуб 4 из таб.1 при конвективной сушке дубового образца размером в поперечном сечении 20x82 мм(0,02 х 0,082 мм), имеющего влажность 29 % в воздухе, движущемся со скоростью 2,0 м/с, при температуре t0=75 °С и ![]() = 0,3 до влажности 9 %.
= 0,3 до влажности 9 %.
Найдем коэффициент влагопроводности а' для образца Дуб 4. Базисная плотность дуба равна ![]() = 560 кг/м3. По левой половине диаграммы коэффициента влагопроводности древесины в тангенциальном направлении (см. рис.1) устанавливаем, что при температуре 75°С и базисной плотности
= 560 кг/м3. По левой половине диаграммы коэффициента влагопроводности древесины в тангенциальном направлении (см. рис.1) устанавливаем, что при температуре 75°С и базисной плотности ![]() = 560 кг/ м3 коэффициент влагопроводности равен
= 560 кг/ м3 коэффициент влагопроводности равен
a’=6,2∙10-6 см2/с.
Приведенная толщина S определена равенством (1) и равна
S= 2 см.
Равновесная влажность древесины в воздухе данного состояния Wp=5,3 % [4;6]. Величину В считаем равной
В≈0,81
Для определения времени сушки от начальной влажности Wн=29 % до влажности Wк= 9 % воспользуемся формулой
![]()
Подставляя имеющиеся значения для четвертого образца Дуб 4, получим
![]()
Получили, что при конвективной сушке четвертого образца Дуб 4 время сушки в 3,65 раза больше, чем при вакуум-импульсной сушке.
Выводы
Приведенные примеры показывают, что эффективность вакуум-импульсной сушки гораздо выше, чем конвективной.
Следует отметить, что предлагаемая автором Расевым А.И. [4] формула определения времени сушки
![]()
Работает не всегда, а только в случае, когда выполняется неравенство
0,81∙Wн+0,19∙Wр>Wк.
Это создает определенные неудобства, так как данная формула не позволяет определять время сушки пошагово по влажности.
Пусть
Wн=28 %; Wк= 25 %; Wр= 5 %.
Рассмотрим величину
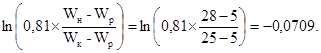
но тогда время сушки будет отрицательным, чего быть не может. В этом случае, что нетрудно проверить, не выполняется неравенство
0,81∙Wн+0,19∙Wр>Wк.
Рецензенты:
Старжинский В.Н., д.т.н., Уральского государственного лесотехнического университета кафедры Охрана труда, г. Екатеринбург;
Уласовец В.Г., д.т.н., профессор кафедры механической обработки древесины Уральского государственного лесотехнического университета, г. Екатеринбург.



