Метод тепловой линзы широко используется в термооптической спектрометрии, в оптической диагностике материалов [8–10]. В жидких двухкомпонентных средах термолинзовый отклик имеет свои особенности, поскольку, кроме обычного теплового отклика, связанного с тепловым расширением среды, здесь могут возникать концентрационные потоки, обусловленные явлением термодиффузии (эффекта Соре) [1–7]. При этом перераспределение концентрации компонент в неоднородном световом поле приводит к соответствующему изменению показателя преломления (и поглощения) среды.

В работе [2] предложена новая схема термолинзовой ячейки с тонкослойной кюветой, толщина которой значительно меньше размера светового пучка. При этом тепловая задача решается с учетом только потоков через окна кюветы. Для двухкомпонентной среды при расчете светоиндуцированной линзы дополнительно необходим учет радиальных концентрационных потоков.

Цель исследования

В данной работе теоретически исследован стационарный термолинзовый отклик двухкомпонентной жидкофазной среды в тонкослойной кювете.

Рассмотрим однолучевую схему измерения термолинзового сигнала (рис. 1). Пусть двухкомпонентная жидкофазная среда, коэффициент поглощения которой целиком определяется одним компонентом с массовой концентрацией (где – константа среды), находится в тонкой кювете толщиной .

Для нахождения параметров тепловой линзы рассмотрим тепловую задачу нагрева среды лазерным пучком. Считая, что для малых толщин слоя среды и окна кюветы (при ) можно пренебречь радиальным (вдоль ) тепловым потоком, получаем из одномерную тепловую задачу:

, (1)

где — удельные теплоемкость и плотность среды, — температура среды, — коэффициент теплопроводности среды, — интенсивность падающего излучения ( считаем поглощение малым ( ).

Для гауссова пучка распределение интенсивности падающего излучения в плоскости, перпендикулярной оптической оси z:

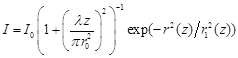, (2)

где 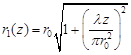- радиус пучка на расстоянии от перетяжки, r – расстояние от оси пучка, — длина волны излучения, — радиус пучка в перетяжке, — интенсивность излучения на оси в плоскости перетяжки пучка.

Аналогично рассматривается тепловая задача для температуры в окне кюветы :

, (3)

где — теплофизические параметры материала окна.

Граничные условия на границе кювета-воздух соответствуют, например, конвективному теплообмену:

. (4)

где — соответственно коэффициент конвективного теплообмена и температура внешней среды, . На границе раздела среда кювета имеем условия равенства температур и тепловых потоков:

. (5)

. (6)

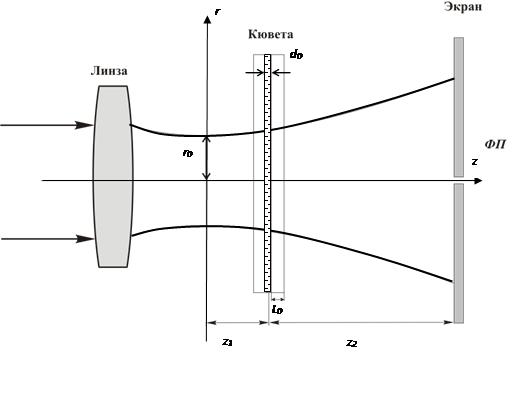
Рис. 1. К расчету термолинзового отклика среды в тонкослойной цилиндрической кювете

В стационарном режиме имеем следующие решения системы (1–6) для распределения температур в среде и окне кюветы :

, (7)

, (8)

. (9)

Теперь учтем влияние термодиффузии. Поскольку диффузионные процессы намного порядков медленнее, чем процессы теплопереноса, можем считать, что термодиффузия поглощающей компоненты происходит в квазистационарном температурном поле, которое определяется формулами (7–9), но уже с зависящим от концентрации коэффициентом поглощения.

Систему балансных уравнений для концентрации поглощающих частиц запишем следующим образом:

, (10)

(11)

где: – концентрационный поток, – коэффициент диффузии поглощающих частиц, – коэффициент термодиффузии. Для толщин слоя можем пренебречь изменением температуры в слое среды по толщине кюветы и принять ее равной . В установившемся режиме () из (10–11) имеем для стационарного значения концентрации:

(12)

Считая изменение концентрации поглощающей компоненты малым по сравнению с начальным, имеем где . Тогда из (12) с учетом (8) получаем линеаризованное уравнение по:

(13)

где: , .

Из (13) получаем:

(14)

Для расчета термолинзового сигнала используем выражение для линзовой прозрачности кюветы [10]:

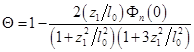, (15)

где , — нелинейный набег фаз в оптической ячейке на оси пучка. Последний включает два вклада, обусловленных термолинзой в слое среды и в окнах кюветы:

. (16)

, (17)

где и постоянные коэффициенты для нелинейной среды и материала окна соответственно, — волновой вектор излучения.

Используя (15–17), получаем:

. (18)

. (19)

Окончательно для стационарного значения линзовой прозрачности кюветы имеем выражение:

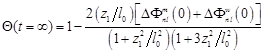. (20)

Полученное выражение позволяет рассчитать влияние термодиффузии на величину стационарного термолинзового отклика тонкослойной оптической ячейки с двухкомпонентной средой.

Выводы

Таким образом, показано, что термолинзовый отклик в двухкомпонентной среде содержит дополнительный вклад, обусловленный термодиффузионным изменением концентрации поглощающей компоненты. Величина этого вклада может быть достаточно большой и иметь разный знак для разных сред в зависимости от знака коэффициента термодиффузии. Также на величину стационарного термолинзового отклика будет влиять и изменение пропускания слоя среды. Таким образом, самоиндуцированную модуляцию коэффициента поглощения необходимо учитывать при анализе данных в термолинзовой спектроскопии многокомпонентных сред [1–3]. Полученные выражения могут быть использованы при экспериментальном определении величин коэффициентов тепломассопереноса в многокомпонентных жидкофазных средах [5–8].

Рецензенты:

Карпец Ю.М., д.ф.-м.н., профессор кафедры «Физика и теоретическая механика» ФГБОУ ВПО «Дальневосточный государственный университет путей сообщения», г. Хабаровск;

Криштоп В.В., д.ф.-м.н., профессор по кафедре физики, проректор по учебной работе ФГБОУ ВПО «Дальневосточный государственный университет путей сообщения Министерства транспорта РФ» , г. Хабаровск.