На сегодняшний день разработано множество методов и средств оценки и повышения надежности программного обеспечения. Существуют несколько подходов к обеспечению необходимого уровня надежности программ, основанных на избыточности: временной, информационной, программной. В свою очередь, основными подходами при обеспечении заданного уровня надежности за счет программной избыточности являются мультиверсионное программирование и блоки восстановления [1, 3].
При обоих подходах для решения критичной задачи разрабатывается или приобретается у сторонних разработчиков несколько функционально эквивалентных программных компонентов. Во втором случае они именуются COTS-компонентами (от англ. commercial off-the-shelf – коробочный программный продукт).
Фактически при реализации программного обеспечения по схеме блоков восстановления используются основные идеи метода контрольных точек и рестарта для компонент программного обеспечения таким образом, что в случае ошибки или отказа одного программного компонента исполняется другой функционально эквивалентный ему программный компонент [9]. В рамках схемы блоков восстановления такие программные компоненты называются альтернативами. Оценка корректности результата выполняется в контрольной точке посредством приемочного теста [8]. Именно здесь принимается решение о целесообразности выполнения другой альтернативы в случае ошибки первой.
Мультиверсионное (или N-вариантное программирование) предполагает одновременное выполнение всего набора функционально эквивалентных программных компонентов [4, 10]. В рамках данного подхода программные компоненты называются версиями. Результаты, возвращенные версиями, оцениваются в контрольной точке, например, посредством голосования абсолютным большинством [6]. Именно здесь определяется корректный результат.
Для обоих подходов справедливо предположение, что потенциальные ошибки могут возникнуть в разных точках исполнения программных компонент. Основой данного предположения служит то, что, и альтернативы, и версии реализуют различные алгоритмы и методы решения одних и тех же задач. Это гарантирует, что ошибки отдельных программных компонент, не выявленные на этапе тестирования, не приведут к отказу всей программной системы, даже в случае отказа отдельных ее компонент [4].
Очевидно, что оба подхода, основываясь на программной избыточности, требуют дополнительных ресурсов на разработку и реализацию программного обеспечения [2, 5]. Это приводит к необходимости решения задачи выбора оптимального состава избыточного программного обеспечения, при котором было бы гарантирован максимальный уровень надежности, с одной стороны, учтены существующие ограничения на ресурсы, с другой стороны.
Схема блока восстановления с согласованием
Рассмотрим подход, комбинирующий мультиверсионное программирование и схему блоков восстановления – схему блока восстановления с согласованием. Данная схема объединяет достоинства двух исходных подходов с целью повышения надежности программного обеспечения.
Предположим, что необходимо выбрать оптимальный набор программных компонент, т. е. оптимальный состав программной системы, которая выполняет ряд функций. Выполнение определенной функции программной системы осуществляется модулями данной системы. Обозначим архитектуру программной системы как S, а количество функций, которые должна выполнять программная система, как L, тогда sl – множество модулей, необходимых для выполнения функции l, sl ∈ S, l ∈ L. Обозначим частоту использования функции l как fl.
Согласно схеме блоков восстановления каждый из n модулей программной системы состоит из mi альтернатив, i = 1, 2, …, n. Однако в схеме блока восстановления с согласованием каждая альтернативу будем рассматривать как мультиверсионную, т. е. каждая альтернатива будет представлена набором версий. Обозначим количество версий, реализующих альтернативу j модуля i, как Vij.
Модель оптимизации выбора компонентов программной системы
Формализуем задачу выбора компонентов программной системы, разрабатываемой согласно схеме блока восстановления с согласованием. Модель оптимизации выбора компонентов может быть записана следующим образом:
![]()
при условиях:
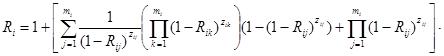
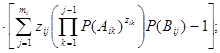
![]()
![]()
![]()
![]()
![]() и
и![]()
![]()
![]() и
и![]()
![]()
![]() и
и![]()
где R – надежность (вероятность безотказной работы) программной системы; Ri – надежность модуля i; Rij – надежность альтернативы j модуля i; xijk – булева переменная, равная 1, если выбрана k-я версия j-й альтернативы модуля i, созданная сторонними разработчиками (COTS-компонент), 0 – иначе; yij – булева переменная, равная 1, если j-я альтернатива модуля i разрабатывается собственными силами, 0 – иначе; zij – булева переменная, равная 1, если j-я альтернатива присутствует в модуле i, 0 – иначе; Aij – событие, соответствующее отклонению результата альтернативы j модуля i; Bij – событие, соответствующее принятию корректного результата альтернативы j модуля i; p1 – вероятность того, что следующая альтернатива не будет вызвана, несмотря на сбой текущей альтернативы; p2 – вероятность неверной оценки корректного результата; p3 – вероятность принятия неверного результата за корректный; Nij+ – количество успешно пройденных тестов; Nij – общее количество тестовых испытаний; qij – вероятность того, что единичное исполнение альтернативы j модуля i не пройдет тест.
Следует отметить, что если альтернатива для модуля i приобретается (т. е. xijk = 1), тогда внутренняя разработка компонента отсутствует (т. е. yij = 0) и наоборот [7]:
![]()
![]()
![]()
В том случае, если используется COTS-компонент, т. е. программный компонент приобретается, то информация о характеристиках компонента и, в том числе, о его надежности предоставляется поставщиком. Таким образом, надежность Rij альтернативы j модуля i программной системы можно представить в виде:
![]()
![]()
![]()
где Rijk – надежность версии k альтернативы j модуля i.
При создании программной системы гарантируется избыточность обоих типов компонентов, как компонентов собственной разработки, так и готовых COTS-компонентов:
![]()
![]()
![]()
![]()
![]()
Стоимость самостоятельной разработки альтернативы j модуля i можно выразить как cij(tij + τijNij), где cij – стоимость единичной разработки альтернативы j модуля i; tij – расчетное время разработки альтернативы j модуля i; τij – среднее время, требуемое на выполнение тестового сценария для альтернативы j модуля i. Тогда общие расходы на разработку и закупку компонент программной системы C должны удовлетворять условию:
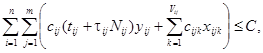
где cijk – стоимость версии k альтернативы j модуля i.
При выборе компонентов программной системы особое внимание стоит уделить сроку поставки готовых компонентов. Срок поставки версии k альтернативы j модуля i dijk указывается поставщиком. Время же собственной разработки компонентов (tij + τijNij) рассчитывается группой разработчиков программной системы.
В реальных условиях довольно сложно получить точные значения этих параметров, так как в процессе разработки или при приобретении компонентов необходимо учесть много факторов. Как правило, эти значения рассчитываются на начальных этапах разработки программной системы. Так, время, требуемое для создания программной системы, определяется временем интеграции различных компонентов в состав программной системы, временем тестирования системы, временем поставки COTS-компонентов. На время создания программной системы влияют такие факторы, как состав группы разработчиков, стратегия тестирования, среда тестирования, доступность компонент на рынке сбыта, сведения о профессиональной квалификации поставщика т. д. При этом точный срок поставки компонентов для разработки программной системы определить достаточно сложно модульной. Вследствие чего приходится закладывать в срок поставки определенный уровень допустимого отклонения. Таким образом, ограничение на срок разработки программной системы может быть записано следующим образом:
![]()
![]()
![]()
где T – максимальный срок разработки программной системы, определяемый проектировщиком системы.
Решение задачи оптимизации состава избыточной программной системы, создаваемой согласно схеме блока восстановления с согласованием, может быть получено с помощью хорошо известных методов дискретной оптимизации или методов принятия решений [4]. Следует отметить, что ряд параметров может быть представлен в виде нечетких чисел, например, сроки поставки готовых программных компонент или время тестирования программной системы. В этом случае решение может быть получено при помощи методов и алгоритмов нечеткой оптимизации [7].
Заключение
Проблема обеспечения высокого уровня надежности программных систем всегда остро стоит перед проектировщиками и разработчиками, и успех ее решения во многом определяет эксплуатационные характеристики создаваемых программных систем. Наряду с классическими методами тестирования и отладки программного обеспечения существенный вклад в повышение надежности вносят новые подходы к структурному построению и выбору состава программных систем. Рассмотренный в данной статье подход позволяет повысить надежность программной системы за счет программной избыточности, применение которой, в свою очередь, приводит к дополнительным затратам. В статье предложена модель, формализующая проблему формирования оптимальной программной системы по схеме блока восстановления с согласованием, которая учитывает наиболее важные ограничения при создании программных систем. Особенностью данной модели является учет возможности формирования программной системы на базе, как готовых программных компонент, так и компонент собственной разработки. Потенциальной областью применения предложенной модели является создание программных систем, к которым предъявляются высокие требования по надежности.
Рецензенты:
Бронов С. А., д.т.н., профессор, руководитель научно-учебной лаборатории систем автоматизированного проектирования кафедры систем искусственного интеллекта Сибирского федерального университета, г. Красноярск.
Ченцов С. В., д.т.н., профессор, зав. кафедрой «Системы автоматики, автоматизированное управление и проектирование» Сибирского федерального университета, г. Красноярск.



