Модель синхронного генератора с демпферными контурами описывается системой из шести дифференциальных уравнений. Два первых дифференциальных уравнения записываются для поперечной и продольной обмоток статора. Три следующих уравнения записываются для обмоток ротора. В обмотки ротора входят поперечная и продольная демпферные обмотки и обмотка возбуждения. Шестое дифференциальное уравнение является нелинейным. Это уравнение описывает связь инерционного, электромагнитного и механического моментов, действующих на вал ротора [1, 5]. Решение этих уравнений является непростой задачей. Однако искусство моделирования состоит не в умении решать сложные уравнения, а в умении без потерь основных, главных свойств явления преобразовывать исходную сложную систему в более простую, руководствуясь при этом условиями которым подвержена исследуемая система. Поэтому цель работы состоит в исследовании моделей генератора в условиях, когда исходную сложную систему можно упростить, но при этом не потерять основные характерные особенности модели [4].
Машина без демпферных обмоток с АРВ сильного действия.
Рассмотрим переходный процесс при внезапном изменении момента первичного двигателя синхронной машины на величину ∆Мт. Для упрощения будем считать, что машина не имеет демпферных обмоток, не будем учитывать явнополюсность и пренебрегаем величиной активного сопротивления статора R. В этом случае уравнения могут быть записаны в следующем виде:
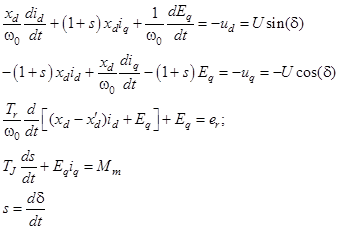(1)
Здесь 
– синхронная ЭДС по поперечной оси, величина пропорциональна току возбуждения 
. Эта величина подлежит определению. 
– постоянная времени контура возбуждения при замкнутых контурах цепи статора. 
– продольный и поперечный токи статора. 
– ЭДС пропорциональная напряжению статора. 
– основные технические данные машины: синхронные реактивные сопротивления по поперечной и продольной осям, переходное сопротивление по продольной оси, активное сопротивление обмотки статора соответственно [6].
Искомые переменные в уравнениях 1: 
– продольный и поперечный токи статора и синхронная ЭДС 
.
Для того чтобы выяснить смысл составляющих напряжения на зажимах машины Ud и Uq в случае примыкания ее к некоторым шинам, напряжение которых мы будем считать имеющим постоянную амплитуду U и синхронную частоту ωo, рассмотрим векторную диаграмму на рис. 1. На этом рисунке изображены поперечная и продольная оси ротора, вращающиеся со скоростью 
и изображающий вектор напряжения шин, вращающийся со скоростью ω0. Из приведенного рисунка следует, что 
Кроме того, из того же рисунка видно, что разность скоростей поперечной оси ротора и изображающего вектора напряжения шин равна производной угла δ, т. е. 
, где s – скольжение машины. Скольжением машины называется величина, равная разности угловой скорости ω1 вращающегося магнитного поля, создаваемого переменным током, протекающим в обмотках статора, и угловой скорости ω ротора машины, отнесённой к ω1 : s = (ω1 - ω)/ω1 [4].
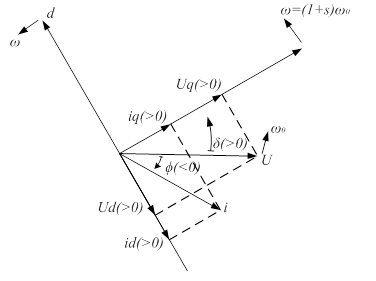
Рис. 1. Векторная диаграмма для определения составляющих напряжения приемных шин по осям q и d
Положим, что в нормальном режиме, предшествующем возмущению, величины токов iq и id, э. д. с. возбуждения Eq, угол δ и скольжение s были равны соответственно 
, 
, 
, 
, 
. Так как в нормальном режиме все эти величины являются постоянными, то они могут быть определены из выше приведенных уравнений, в которых все производные должны быть равны нулю. Поэтому уравнения, определяющие переменные в нормальном режиме, принимают вид:
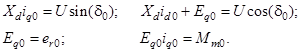(2)
Уравнения (1), являются нелинейными, и решить их операторным методом невозможно. Такое решение может быть, однако, выполнено, если приближенно принять, что отклонения переменных от их начальных значений оказываются в переходном процессе настолько малы, что нелинейные члены в уравнениях (1) могут быть заменены их линейными приближениями. В нашем случае это означает, что изменение момента турбины первичного двигателя, вызывающее переходный процесс, должно быть достаточно мало. Предполагая, что последнее условие выполняется, введем новые переменные, равные отклонениям основных переменных от их значений в нормальном режиме:
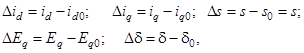
а также отклонения внешних сил от их начальных значений:
В новых переменных нелинейные члены уравнений (1) могут быть представлены в следующем виде:
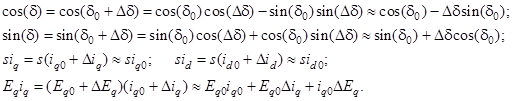
При выводе последних приближенных выражений для нелинейных членов мы пренебрегли квадратами, произведениями и более высокими степенями приращений ∆id, ∆iq и т. д. [4].
Подставляя полученные выражения в уравнения (1) и учитывая уравнения (2), которыми определяются начальные значения всех переменных, получим следующие линейные уравнения относительно приращений основных переменных:
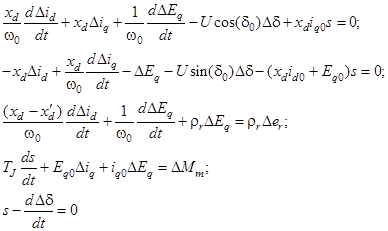(3)
Здесь 
– инерционная постоянная машины. 
– отношение механического момента к базисному моменту. 
– декремент контура ротора.
Будем решать уравнения (3), предполагая наличие безынерционного регулирования возбуждения машины по закону
и считая, что приращение момента первичного двигателя ∆Mт, возникнув в момент t = 0, в дальнейшем остается неизменным.
Коэффициенты k, k’ и k” называются регулирующими. Величины этих коэффициентов выбирают таким образом, чтобы члены, в которые они входят, были бы соизмеримыми с остальными членами в коэффициентах уравнений. В соответствии с этим коэффициент k” должен иметь порядок 
т.е. 103 (при Tj = 10 сек и ωо = 314 будем иметь 
). Коэффициент k` должен иметь порядок 1/ρr, т. е. также 103 (при Tr = 5сек будем иметь 
). Наконец, коэффициент k должен иметь порядок единицы [5].
Приняв значения коэффициентов регулирования, перейдем к решению уравнений. Данные уравнения решаем с помощью программы MathCAD.
Приведем расчет для генератора с паспортными данными в таблице 1.
Таблица 1
Паспортные данные генератора
|
|
|
|
|
|
|
|
1,318 |
0,865 |
5 |
8. |
36о |
1,115 |
, град
Первый этап – определение принужденных составляющих. Система уравнений (1) является нелинейной. Чтобы определить точки положения равновесия 
, необходимо решить стационарное уравнения, приняв все производные в системе уравнений равными нулю и считая отклонения от положения равновесия малыми 
.
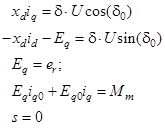(4)
С учетом наличия безынерционного регулирования возбуждения машины получаем выражения для установившегося режима с помощью программно - интегрированной среды MathCAD с использованием функций Given и Find [2]:
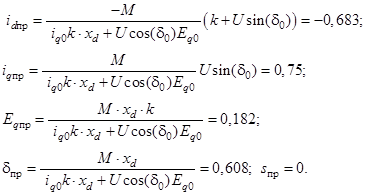
Второй этап – это решения системы дифференциальных уравнений методом пространства состояний. Приводим уравнения (3) к нормализованной форме, разрешая их относительно производных, получаем матрицу состояний и вектор правых частей:
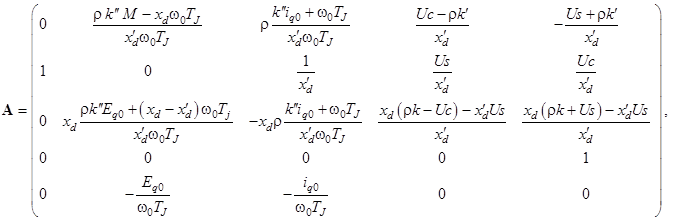
Выбор настроечных коэффициентов.
Коэффициент 
изменяется в пределах единицы. Этот коэффициент препятствует «сползанию» системы. (Большая нагрузка генератора и подход к предельным значениям мощности и угла. Характеризуется вначале медленным, а затем быстрым увеличением угла и выпадением из синхронизма с последующим разрывом передачи). Увеличение коэффициента уменьшает сползание. Однако дальнейшее увеличение этого коэффициента приводит к раскачиванию системы. (Самораскачивание обычно интенсивнее в явнополюсных машинах; при большом возбуждении и работе на большое активное сопротивление. Это может привести к изменению знака демпферной мощности).
Коэффициенты регулирования по производным угла 
не влияют на возникновения сползания, но препятствуют возникновению самораскачивания. При значениях 
система является устойчивой. Наиболее оптимальные значения являются 
[4].
Коэффициент регулирования по второй производной угла 
может изменяться в широких пределах. Для его оптимального выбора был использован корневой годограф. Его оптимальное значение показано на рисунке 2. Оптимальные значения корней выделены зелеными и сиреневыми квадратами. Оптимальные значения настроечного коэффициента при этом равны 
.
В качестве сравнения приведены фазовые портреты (скольжение – угол) переходных процессов с различными регулировочными коэффициентами.
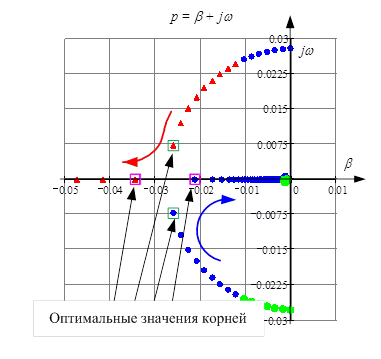
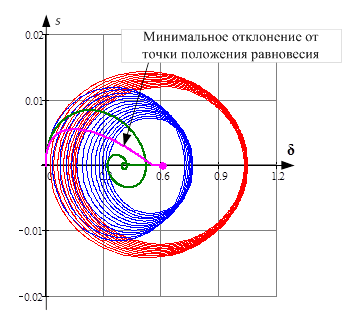
Рис. 2. Корневой годограф
Для неоптимальных коэффициентов область, охватываемая замкнутой фигурой, имеет большую площадь, то есть наибольшее отклонение параметров от положения равновесия. Замкнутость фигур с уменьшающимся радиусом свидетельствует о колебании системы. Для оптимальных коэффициентов кривая имеет минимальное отклонение от точки положения равновесия (сиреневая кривая).
Применение моделей возможно не только в учебном процессе для изучения переходных процессов в сетях содержащих синхронные генераторы, но и для проектирования объектов, содержащих генераторы, в расчетах будут выбираться соответствующие модели в зависимости от расположения приложения точки возмущения переходного процесса.
Рецензенты:
Усов Ю.П., д.т.н., профессор кафедры ЭСиЭ ЭНИН ФГБОУ ВПО «НИ ТПУ», Национальный исследовательский Томский политехнический университет, г. Томск;
Сивков А.А., д.т.н., профессор кафедры ЭПП ЭНИН ФГБОУ ВПО «НИ ТПУ», Национальный исследовательский Томский политехнический университет, г. Томск.