В теории сетей массового обслуживания фундаментальным является понятие состояния сети, при этом важнейшей характеристикой таких сетей являются вероятности их состояний, которые используют для определения наиболее значимых системных параметров информационных сетей, таких как:
- производительность;
- время доставки пакетов;
- вероятности потери сообщений и блокировки в узлах;
- области допустимых значений нагрузки, при которых обеспечивается требуемое качество обслуживания и др.
Базовая сеть коммутации пакетов состоит из множества топологически распределенных узлов коммутации, связанных между собой каналами передачи данных. Абоненты базовой сети являются источниками и потребителями информации, передаваемой посети (рис. 1). Основная информационная единица базовой сети - пакеты данных - передается от источника к адресату через каналы, образуя очереди в буферной памяти узлов коммутации.
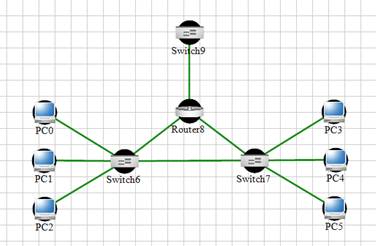
Рис. 1. Пример топологии локальной компьютерной сети.
Адекватными моделями сетей пакетной коммутации являются сети массового обслуживания. Основная задача моделирования состоит в анализе наиболее важных характеристик базовой сети передачи данных, таких как производительность сети и средняя задержка пакетов. Часто представляет интерес и расчет средней задержки между выделенной парой «источник-адресат».
На характеристики сети существенное влияние оказывают протоколы передачи данных. Для обеспечения надежности передачи информации в протоколах различных уровней реализуются механизмы квитирования и периоды ожидания (time-out). В первую очередь следует выделить межконцевое (сквозное) квитирование между источником и адресатом. Копия передаваемого сетью пакета сохраняется в памяти источника до получения квитанции обуспешной доставке. Отсутствие квитанции в течение интервала времен time-out приводит к передаче копии из источника.
Квитирование может также осуществляться и между соседними узлами коммутации пакетов. При этом копия пакета сохраняется в буферной памяти передающего узла коммутации до получения квитанции от соседнего узла. По истечении интервала time-out осуществляется повторная передача пакета по тому же выходному каналу или изменение маршрута.
Различные методы квитирования и ограниченный объем буферной памяти узла коммутации, оказывающие существенное влияние на характеристики базовой сети передачи данных, должны находить отражение в соответствующих моделях сетей массового обслуживания.
Применяемые в настоящее время в локальных сетях протоколы канального уровня используют методы доступа к среде, основанные на ее совместнойэксплуатации несколькими узлами за счет разделения во времени. В этом случае, как и во всех случаях разделения ресурсов со случайным потоком запросов, могут возникать очереди. Для описания этого процесса обычно используются модели теории массового обслуживания.
При аналитическом моделировании исследование процессов или объектов заменяется построением их математических моделей и исследованием этих моделей. В основу метода положены идентичность формы уравнений и однозначность соотношений между переменными в уравнениях, описывающих оригинал и модель. Поскольку события, происходящие в локальных вычислительных сетях, носят случайный характер, то для их изучения наиболее подходящими являются вероятностные математические модели теории массового обслуживания.
Аналитическая модель сети представляет собой совокупность математических соотношений, связывающих между собой входные и выходные характеристики сети. При выводе таких соотношений приходится пренебрегать какими-то малосущественными деталями или обстоятельствами [1].
Телекоммуникационная сеть при некотором упрощении может быть представлена в виде совокупности процессоров (узлов), соединенных каналами связи. Сообщение, пришедшее в узел, ждет некоторое время до того, как оно будет обработано. При этом может образоваться очередь таких сообщений, ожидающих обработки. Время передачи или полное время задержки сообщения D равно:
D = Tp + S + W, (1)
где Tp, S и W соответственно время распространения, время обслуживания и время ожидания. Одной из задач аналитического моделирования является определение среднего значения D. При больших загрузках основной вклад дает ожидание обслуживания W. Для описания очередей в дальнейшем будет использована нотация Д. Дж. Кенделла:
A/B/C/K/m/z,
где А – процесс прибытия;
В – процесс обслуживания;
С – число серверов (узлов);
К – максимальный размер очереди (по умолчанию – ∞);
m – число клиентов (по умолчанию – ∞);
z – схема работы буфера (по умолчанию FIFO).
Буквы А и В представляют процессы прихода и обслуживания и обычно заменяются следующими буквами, характеризующими закон, соответствующий распределению событий:
D – постоянная вероятность;
M – марковское экспоненциальное распределение;
G – обобщенный закон распределения;
Ek – распределение Эрланга порядка k;
Hk– гиперэкспоненциальное распределение порядка k.
Наиболеераспространеннымисхемамиработыбуферовявляются FIFO (First-In-First-Out), LIFO (Last-In-First-Out) и FIRO (First-In-Random-Out). Например, запись M/M/2 означает очередь, для которой времена прихода и обслуживания имеют экспоненциальное распределение, имеется два сервера, длина очереди и число клиентов могут быть сколь угодно большими, а буфер работает по схеме FIFO[2].
Механизм разделения среды протокола Ethernet упрощенно описывается простейшей моделью типа M/M/1 - одноканальной моделью с пуассоновским потоком заявок и показательным законом распределения времени обслуживания. Она хорошо описывает процесс обработки случайно поступающих заявок на обслуживание системами с одним обслуживающим прибором со случайным временем обслуживания и буфером для хранения поступающих заявок на время, пока обслуживающий прибор занят выполнением другой заявки. Передающая среда Ethernet представлена в этой модели обслуживающим прибором, а пакеты соответствуют заявкам.
На рис. 2 приведена простейшая схема такой системы. Она содержит буфер, который может хранить очередь бесконечной длины, состояние которой может быть отождествлено с числом заявок, содержащихся в очереди в каждый момент времени.
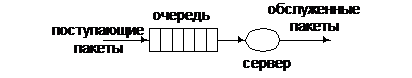
Рис. 2. СМО типа М/М/1.
Поскольку входной процесс одинарный, то в каждый момент времени к очереди может добавиться только одна заявка.Поскольку сервер один, то в каждый момент времени может быть обслужена, то есть уйти из очереди, только одна заявка. Таким образом, рассматриваемая СМО относится к процессу класса «гибели-размножения». Для анализа необходимо конкретизировать параметры системы. Распределение вероятностей входного потока и времени обслуживания позволяет полагать интенсивности вероятностей в модели постоянными.
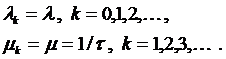 (2)
(2)
(3)
Здесь t – среднее время обслуживания на сервере.
Общее решение позволяет сразу записать вероятность того, что в стационарном состоянии в очереди будет находиться k заявок
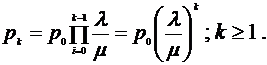 |
(4)
Найдем начальное значение вероятности, учитывая сходимость соответствующего ряда
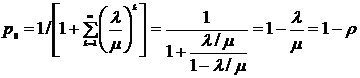
(5)
![]() Окончательно получаем формулу для
вероятности длины очереди
Окончательно получаем формулу для
вероятности длины очереди
(6)
На рис. 3 приведен график вероятностей того, что в очереди находится k заявок в установившемся режиме.
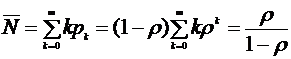 Важной характеристикой системы является
средняя длина очереди. Зная вероятности каждого из возможных значений длины,
найдем математическое ожидание:
Важной характеристикой системы является
средняя длина очереди. Зная вероятности каждого из возможных значений длины,
найдем математическое ожидание:
(7)
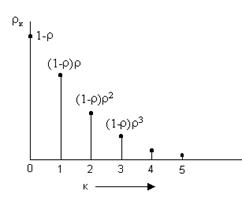
Рис. 3. Стационарные вероятности рк для СМО типа М/М/1.
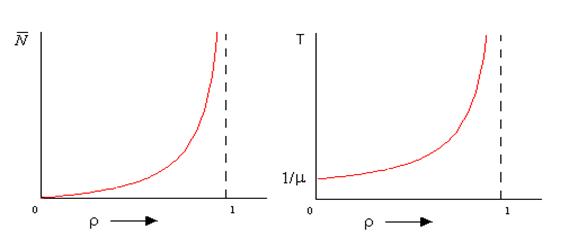
График средней длины очереди заявок в системе в зависимости от значения коэффициента использования или нагрузки показан на рис. 4.
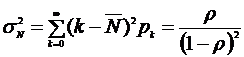 Найдем дисперсию длины очереди:
Найдем дисперсию длины очереди:
(8)
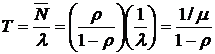 Для нахождения среднего значения времени
пребывания в очереди воспользуемся формулой Литтла.
Для нахождения среднего значения времени
пребывания в очереди воспользуемся формулой Литтла.
(9)
На рис. 5 приведен график зависимости среднего времени пребывания в очереди в зависимости от коэффициента использования (нагрузки).
Рассматривая полученные результаты, можно увидеть, что при увеличении коэффициента использования как длина очереди, так и время пребывания в ней неограниченно возрастают при приближении ρ к единице. Такой вид зависимости от коэффициента использования характерен для почти всех СМО.
|
Рис. 4. Среднее число требований в системе типа M/M/1. |
Рис. 5. Среднее время пребывания требования в системе типа M/M/1 как функция ρ. |
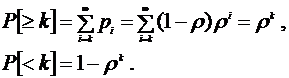 Таким образом, вероятность того, что в
очереди будет находиться не менее чем k заявок, и того, что в очереди менее k
заявок, определяется как:
Таким образом, вероятность того, что в
очереди будет находиться не менее чем k заявок, и того, что в очереди менее k
заявок, определяется как:
(10)
(11)
В ходе анализа простейшей системы М/М/1 возможно в аналитическом виде найти практически все интересные характеристики QoS системы [3-5].
Иногда представляет интерес определение такого показателя, как максимальное время задержки заявки каждого типа в локальной компьютерной сети. Максимальное время – это время, превышение которого допустимо лишь для некоторого, наперед заданного процента заявок каждого типа. Для определения максимального времени используется методика, основанная на аппроксимации функции распределения времени задержки в сети эрланговским или гиперэкспоненциальным распределением, при этом необходимо задавать долю (процент) заявок, для которых рассчитывается максимальное время.
В качестве характеристики производительности коммуникационного оборудования используются единицы кадр/с и бит/с. Чаще используется единицакадр/с, так как для коммуникационного оборудования наиболее тяжелым режимом является обработка кадров минимальной длины. Количество таких кадров,поступающих на устройство в единицу времени, максимально, а на обработкукаждого кадра мост, коммутатор или маршрутизатор тратят примерно одно и тоже время. Другая характеристика производительности коммуникационного оборудования – бит/с – используется реже, так как она не учитывает размер обрабатываемого кадра, а на кадрах максимального размера достичь высокой производительности в бит/с гораздо легче.
При оценке целевой эффективности функционирования локальной компьютерной сети приходится сталкиваться с проблемой множественности показателей целевой эффективности. Известно, что каким-то одним обобщенным показателем ограничиться нельзя. Чем больше показателей участвуют в оценке эффективности процессов функционирования локальной компьютерной сети, тем полнее и глубже оказывается такая оценка, тем более обоснованны решения по совершенствованию и развитию сети, принимаемые на основе анализа факторов и параметров, но тем сложнее и дороже сама оценка. И наоборот, чем меньше показателей привлекается к оценке, тем более поверхностными оказываются результаты оценки и тем менее убедительными будут решения, принимаемые на их основе [6].
Следовательно, при выборе числа показателей для оценки целевой эффективности функционирования локальной компьютерной сети необходимо компромиссное решение. В связи с этим при разработке математических моделей сетей Ethernetв системе автоматизации проектирования «NetworkLab» были использованы такие показатели оценки эффективности функционирования сетей различных топологий, создаваемых для изучения курса сетевых технологий, каквремя передачи или полное время задержки сообщения, пропускная способность канала, длина очереди, производительность, вероятности потери сообщений и блокировки в узлах, области допустимых значений нагрузки, при которых обеспечивается требуемое качество обслуживания.
Рецензенты:
Когут А.Т., профессор, д.т.н., профессор кафедры «Автоматика и системы управления»ОмГУПСа,г.Омск;
Сединин В.И. профессор, д.т.н., зав. каф. САПР СибГУТИ, г.Новосибирск.



