Практически важными задачами в электроэнергетике являются улучшение качества электрической энергии и анализ потерь в линиях электропередачи [7-10]. Решение второй задачи предполагает использование уравнений теплового баланса. Уравнения теплового баланса проводов в общем случае нелинейны (в разных источниках приводятся несколько различающиеся варианты этих уравнений, неодинаковость которых обусловлена принимаемыми допущениями) и поэтому решаются численными [2, 6] или приближенными аналитическими [1, 3, 4] методами. Те и другие имеют известные недостатки: при использовании численных методов затрудняется анализ результатов, а приближенные аналитические методы дают достаточную точность лишь в ограниченном диапазоне исходных данных.
Вместе с тем при теплоотдаче вынужденной конвекцией нелинейность уравнений обусловлена только лучистым теплообменом. Согласно закону Стефана – Больцмана, интенсивность этого теплообмена выражается через четвертые степени температур. Следовательно, уравнение теплового баланса провода при вынужденной конвекции фактически представляет собой алгебраическое уравнение четвертой степени. Такие уравнения поддаются прямому аналитическому решению. Ниже приведены соответствующие формулы и методика расчета.
1. Расчетные формулы
Уравнение теплового баланса провода воздушной линии может быть записано в виде [3]:
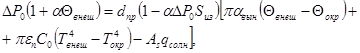(1)
где ΔP0 – потери активной мощности на единицу длины, вычисленные при сопротивлении, приведенном к 0 ºC; α – температурный коэффициент сопротивления; Θвнеш и Θокр – температуры поверхности провода и окружающей среды в ºC; dпр – диаметр провода; Sиз – тепловое сопротивление изоляции на единицу длины провода; αвын – коэффициент теплоотдачи вынужденной конвекцией; εп – коэффициент черноты поверхности провода для инфракрасного излучения; C0 = 5,67·10-8 Вт/(м2·К4) – постоянная излучения абсолютно черного тела; Tвнеш и Tокр – абсолютные температуры поверхности провода и окружающей среды; As – поглощательная способность поверхности провода для солнечного излучения; qсолн – плотность потока солнечной радиации на провод.
Разделим обе части уравнения на 
и перенесем все слагаемые в правую часть с учетом соотношения 
. Тогда после приведения подобных уравнение (1) примет следующий вид:
(2)
Здесь введены следующие обозначения:
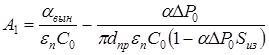, (3)
. (4)
Видно, что выражение (2) представляет собой алгебраическое уравнение четвертой степени относительно температуры Tвнеш. Найдем его решение методом Феррари [5].
Слагаемое, содержащее третью степень неизвестного, отсутствует. Тогда первым шагом решения уравнения методом Феррари является преобразование с помощью вспомогательного параметра β [5]:
(5)
Параметр β выбирается таким образом, чтобы выражение в квадратных скобках было полным квадратом. Это соответствует условию
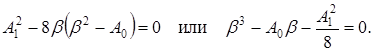(6)
Решая кубическое уравнение (6) по формуле Кардано [5], получим следующее выражение для β:
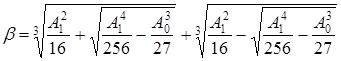. (7)
При таком значении β уравнение (5) сводится к двум квадратным уравнениям:
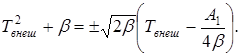(8)
Корни уравнений (8):
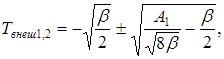(9)
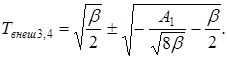(10)
Таким образом, получены формулы для четырех значений температуры, удовлетворяющих исходному уравнению теплового баланса. Очевидно, что реальному режиму соответствует только одно из них, а остальные являются математической абстракцией. Чтобы выбрать «правильный» корень, проведем следующие рассуждения.
1. Предположим, что температурная зависимость сопротивления отсутствует (α=0). Из формул (3), (4) при таком допущении следует, что A1>0, A0<0. Численные расчеты показывают, что такие знаки сохраняются и в реальных условиях при α≠0, по крайней мере при токах, соответствующих нормальным режимам эксплуатации линий.
2. Если A1>0, A0<0, то из формулы (7) видно, что β – действительное положительное число.
3. Так как A1>0 и β>0, то формула (10) дает комплексно-сопряженные корни, а меньший корень, определяемый по формуле (9), представляет собой действительное отрицательное число. Из этого следует, что реальному тепловому режиму линии соответствует больший из корней, определяемых по выражению (9). Таким образом, окончательная расчетная формула для температуры внешней поверхности провода имеет вид
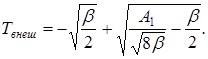(11)
Температура токоведущей части определяется по следующему выражению [10]:
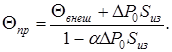(12)
Приведенные формулы справедливы как для изолированных, так и для неизолированных проводов воздушных линий. В последнем случае следует принимать Sиз=0.
2. Пример расчета
Пусть по проводу марки SAX-50 протекает ток 200 А. Исходные данные для расчета (табл. 1) примем те же, что были использованы в [3].
Таблица 1
Исходные данные для расчета температуры провода SAX-50
|
Наименование и обозначение параметра |
Численное значение |
|
Погонное активное сопротивление при 0 ºC r0 |
0,000663 Ом/м |
|
Тепловое сопротивление изоляции на единицу длины Sиз |
0,193566 м∙К/Вт |
|
Температурный коэффициент сопротивления a |
0,0043 ºC-1 |
|
Диаметр провода dпр |
0,0127 м |
|
Коэффициент теплоотдачи вынужденной конвекцией αвын |
13,3764 Вт/(м2∙K) |
|
Степень черноты поверхности провода εп |
0,8 |
|
Поглощательная способность поверхности провода для солнечного излучения As |
0,9 |
|
Температура окружающей среды Θокр |
0 ºC |
|
Плотность потока солнечной радиации qсолн |
526,291 Вт/м2 |
|
Ток в проводе I |
200 А |
Расчет. Потери активной мощности на единицу длины при сопротивлении, приведенном к 0 ºC
Вт/м.
Коэффициенты A1, A0 по формулам (3), (4):
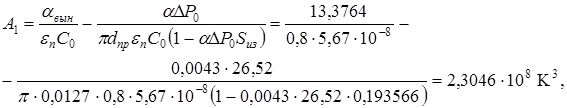
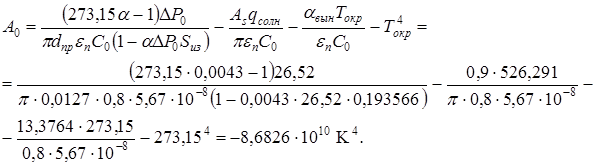
Определяем параметр β по формуле (7):
Температура внешней поверхности провода по формуле (11):
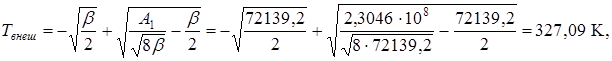
°C.
Температура токоведущей части по формуле (12):
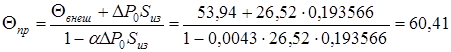°C.
Полученные значения совпадают с результатами численного решения уравнения теплового баланса, приведенными в [3].
Из приведенного расчета видно, что сделанные предположения о знаках коэффициентов для данного примера оказались верными. Однако следует заметить, что это будет справедливо не при любых исходных данных. Так, видно, что при некотором достаточно большом значении потерь мощности (тока) знаменатель во втором слагаемом формулы (3) и в первом слагаемом формулы (4) обращается в ноль. Поэтому коэффициенты A1, A0 при увеличении тока проходят через точки разрыва и меняют знаки. Однако это не свидетельствует о том, что данный метод несправедлив при больших токах, а отражает известный факт, что при больших токах установившегося теплового режима провода не существует. Это является следствием температурной зависимости сопротивления, которая проявляет себя как положительная обратная связь, препятствуя установления теплового равновесия.
Рецензенты:
Черемисин В.Т., д.т.н., профессор, директор Научно-исследовательского института энергосбережения на железнодорожном транспорте, заведующий кафедрой ФГБОУ ВПО «Омский государственный университет путей сообщения», г. Омск;
Кузнецов А.А., д.т.н., профессор, Федерального государственного бюджетного образовательного учреждения высшего профессионального образования «Омский государственный университет путей сообщения», г. Омск.