С развитием информационных технологий физический эксперимент и построенный на его основе традиционный лабораторный практикум существенно преобразились. Можно выделить два основных направления: информатизация натурного эксперимента и включение работ по проведению вычислительного эксперимента.
В первом традиционный лабораторный физический практикум подкрепляется в различной степени компьютерными технологиями. Учащиеся экспериментально исследуют реальные объекты, знакомятся с методами обработки экспериментальных данных, теорией погрешностей, учатся обращению с различными измерительными приборами. Применение информационных технологий заключается в использовании разноцелевого прикладного программного обеспечения: универсальных математических пакетов, электронных таблиц, видео- и аудиоредакторов и др. Специальное программное обеспечение позволяет упростить расчеты, значительно сократив время, необходимое на выполнение рутинных действий. При этом учащиеся применяют навыки, полученные при изучении информатики, для математической обработки экспериментальных данных, вычисления погрешностей, графического представления результатов исследования. Как следствие, возрастает мотивация студентов к самостоятельному изучению и последующему применению различного программного обеспечения для достижения поставленной цели. Тем самым развиваются информационная и научно-исследовательская компетентности [4]. При этом необходимо подчеркнуть, что натурные эксперименты, подкрепленные информационными технологиями, имеют существенный недостаток – ограниченный диапазон варьирования параметров протекания физического эксперимента.
Второе направление информатизации физического эксперимента состоит в использовании компьютера для организации лабораторных работ по компьютерному моделированию и вычислительному эксперименту [5]. Учащиеся на основе математической модели объекта исследования разрабатывают вычислительную модель и проводят с ней серию экспериментов. Изменяя параметры модели, начальные и граничные условия, можно исследовать характерные особенности объекта, прогнозировать его поведение в разнообразных ситуациях. В этом состоит использование математики и компьютера для познания законов реального мира и их применения на практике [2].
Представляется, что необходимым условием для успешного формирования у учащихся глубоких и прочных знаний, практических умений и навыков является координация различных видов учебного эксперимента [1]. Приведем примеры способов организации процесса обучения физике на основе сочетания натурного и вычислительного эксперимента.
1. Параллельное выполнение натурного и вычислительного эксперимента на примере исследования падения тела в вязких и плотных средах.
При движении тел в вязкой жидкости
возникают силы сопротивления. Их происхождение обусловлено двумя различными
механизмами обтекания – ламинарным и турбулентным. При малых скоростях, когда
за телом не образуется вихрей, сила сопротивления определяется только вязкостью
жидкости. В вузовском лабораторном практикуме во время выполнения работы
«Определение коэффициента вязкости глицерина методом падающего шарика»
обтекание свинцового шарика считается ламинарным и силы сопротивления
определяются по формуле Стокса. При этом использование цифровой видеокамеры с
последующим анализом записи в видеоредакторе показывает, что реальное движение
тела является сложным: в начале движения оно будет близким к равноускоренному с
ускорением, почти равным ускорению силы тяжести. Затем ускорение будет
постепенно уменьшаться, и движение станет практически равномерным с
установившейся скоростью 
.
Опыт проведения натурного эксперимента, подкрепленного информационными технологиями, показывает, что падение свинцового шарика радиусом несколько миллиметров в глицерине через 5-8 см становится почти равномерным со скоростью ν. Измеряя эту скорость, можно определить коэффициент вязкости жидкости. При такой организации натурного эксперимента, первый участок движения (с переменной скоростью) остается вне поля исследования. В случае более крупного тела, а также при движении в менее плотных средах (воде, воздухе) обтекание может иметь турбулентный характер. Эти и другие особенности движения тела в вязкой среде целесообразно исследовать в компьютерном эксперименте с использованием поэтапной технологии вычислительной физики [3].
В данной работе параллельное выполнение натурного и вычислительного эксперимента позволяет изучить все этапы движения тела в вязких и плотных средах, что расширяет границы исследования, делает его более целостным и содержательным.
2. Совмещенный натурно-вычислительный эксперимент на примере исследования теплопроводности металлов.
Процессы теплопроводности, как и другие явления переноса, относятся к неравновесным процессам, изучению которых стоит уделять особое внимание. Такие явления обычно экспериментально исследуются при фиксированных (идеализированных) условиях – в стационарных режимах с привлечением сложного лабораторного оборудования.
В данной лабораторной работе предлагается исследовать явление теплопроводности металлов в нестационарном режиме с помощью простого оборудования (рис. 1) и ПК.
Рис. 1. Установка для определения коэффициентов теплопроводности металлов:
1 – нагревательный элемент; 2 – исследуемый металлический стержень; 3 – грузики
равной массы; 4 – парафин.
Распределение температуры вдоль
металлического стержня в отсутствии источников и стоков тепла описывается
классическим уравнением теплопроводности: 
. Для учета стоков (рассеяния в
окружающую среду) тепла необходимо оценить поток тепла 
, отводимого с поверхности стержня.
Поскольку разность температур окружающей среды и тела невелика, то можно
применить уравнение Ньютона: 
, где α
- коэффициент внешней теплопроводности 
, T – температура поверхности стержня, T0 – температура окружающей
среды. При оценке источника тепла qu
предположим, что количество теплоты, производимое им, полностью расходуется на
нагревание: 
. Считая c и m постоянными величинами, и пренебрегая T0 по сравнению с T, получаем: 
.
Таким образом, классическое уравнение теплопроводности примет следующий вид:
.
После ряда преобразований это уравнение приводится к виду:
.
Где χ – коэффициент температуропроводности, T – температура в точке x в момент времени t. Это уравнение положено в основу предлагаемого метода нахождения коэффициента теплопроводности в нестационарном режиме. Оно имеет следующее фундаментальное решение:
.
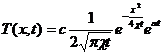Заметим, что температура зависит от времени t, координаты x, а также от характеристик установки (c, α).
В первой части работы ставится фронтальный натурный эксперимент с установкой, представленной на рисунке 1. В ходе эксперимента учащиеся замеряют значение координат x (x1, x2, x3, x4, x5) грузиков и время их выпадения с каждого стержня t (t1, t2, t3, t4, t5).
Во второй части работы студенты производят математическую обработку полученной информации на компьютере с использованием прикладного программного обеспечения. Исходя из того, что выпадение всех грузиков происходит в разное время, но при одной и той же температуре (плавление парафина), можно составить систему из пяти уравнений:
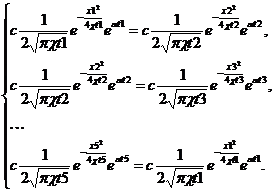
Производя численное решение полученной системы нелинейных уравнений, можно определить характеристики натурной установки α, а затем и c.
Из выражения для температуры 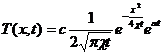видно, что коэффициент
температуропроводности (χ)
не представляется возможным выразить в аналитическом виде, поэтому для его
нахождения также используются методы численного решения при помощи ПК.
Наконец, по известным величинам плотности и удельной теплоемкости образцов можно рассчитать значение коэффициента теплопроводности:
.
Представленная работа подтверждает целесообразность использования в обучении физике такой формы организации исследовательской деятельности студентов, как совмещенный натурно-вычислительный лабораторный эксперимент.
3. Последовательное выполнение натурного и вычислительного эксперимента на примере исследования электростатического поля системы неподвижных зарядов.
Электростатическое поле создается неподвижными точечными зарядами и в каждой точке пространства характеризуется вектором напряженности и потенциалом. Графически такое поле можно представить силовыми линиями и эквипотенциальными линиями или поверхностями.
Экспериментальное изучение электростатического поля сводится к построению карты силовых линий и требует наличия сложной аппаратуры. Поэтому в педагогических вузах происходит изучение натурной модели. Моделирование в таком случае заключается в подмене электростатического поля стационарным электрическим полем, создаваемым в проводящей среде постоянным током между электродами. При этом появляется возможность пользоваться стандартными электроизмерительными приборами. На практике используется следующий прием: экспериментально находятся положения и формы эквипотенциальных поверхностей, а затем, зная, что силовые линии перпендикулярны эквипотенциальным поверхностям, осуществляется построение конфигурации силовых линий.
Исследовательская работа по рассматриваемой теме строится в три этапа:
1) изучение натурной модели;
2) построение вычислительной модели аналогичной натурной;
3) усложнение компьютерной модели и проведение над ней серии вычислительных экспериментов.
На первом этапе студенты получают картины эквипотенциальных поверхностей и силовых линий для плоских и цилиндрических электродов (рис. 2). Использование первых моделирует электростатическое поле конденсатора, вторых – поле двух точечных зарядов одинаковых по величине и противоположных по знаку.
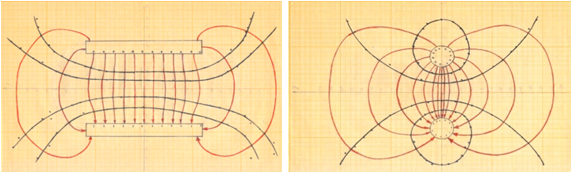
Рис. 2. Карты силовых линий и эквипотенциальный поверхностей (результаты
натурного эксперимента).
Использование такого натурного эксперимента сопровождается двумя ограничениями. Первое – существенные временные затраты для получения качественной картины. Второе ограничение связано с невозможностью исследования электростатического поля от большого числа зарядов. Снять перечисленные ограничения можно путем построения компьютерной модели и проведением над ней вычислительного эксперимента.
Для этого необходимо реализовать следующую последовательность действий:
1) задать количество зарядов, их величины и расположение на плоскости;
2) записать функцию для расчета потенциала электростатического поля:
,
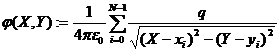где xi, yi – координаты расположения зарядов;
3) задать в пространстве дискретную координатную сетку и рассчитать значение потенциала в ее узлах:
,
где xi, yj – координаты узлов сетки;
4) построить график эквипотенциальных поверхностей (рис. 3, а);
5) построить линии напряженности электростатического поля (рис. 3, б).
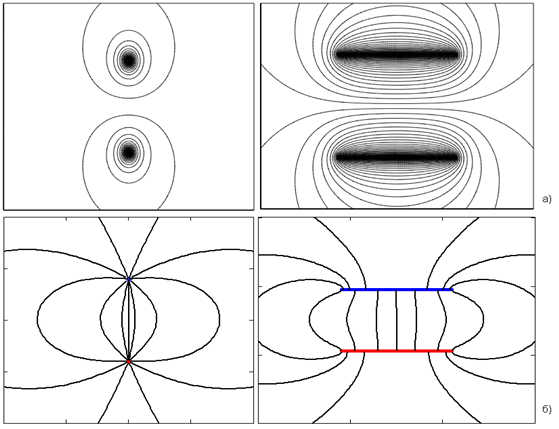
Рис. 3. Результаты вычислительного эксперимента: а) карты эквипотенциальных
поверхностей; б) конфигурация линий напряженности
Сравнение данных натурного и компьютерного экспериментов (изображений электростатического поля, представленных на рис. 2 и 3) можно считать проверкой адекватности компьютерной модели. По результатам сравнения может быть принято решение о необходимости дополнительной корректировки математической модели или о ее достоверности и применимости для моделирования более сложных полей.
На завершающем этапе работы учащиеся выполняют вычислительный эксперимент по изучению электростатического поля сложной конфигурации, образованного большим числом заряженных тел.
Последовательное выполнение различных видов лабораторного эксперимента позволяет расширить границы условий проведения натурного исследования и получить новую информацию о процессах при реализации вычислительного эксперимента.
Учебная практика показывает, что сочетание натурного и вычислительного эксперимента позволяет: повысить предметный уровень обучения студентов благодаря комплексному изучению физических объектов и явлений; показать будущим учителям новые возможности организации обучения за счет внедрения современных информационных технологий в лабораторный физический эксперимент; качественно изменить представления студентов о компьютерном моделировании через проведение аналогии между натурным и вычислительным экспериментом.
Рецензенты:Усольцев А.П., д.п.н., профессор, заведующий кафедрой теории и методики обучения физике, технологии и мультимедийной дидактики, ФГБОУ ВПО «Уральский государственный педагогический университет», г. Екатеринбург.
Ходанович А.И., д.п.н., профессор, заведующий кафедрой математики и физики ФГБОУ ВО «Санкт-Петербургский государственный институт кино и телевидения», г. Санкт-Петербург.