Повышение производительности и увеличении сроков службы машин и механизмов требует постоянного улучшения конструкции и технологии производства подшипников качения, повышения их грузоподъемности и долговечности. В машино- и автомобилестроении широко применяются конические роликовые подшипники, обеспечивающие надежную работу вращающихся узлов при радиальных и осевых нагрузках. Долговечность подшипника в значительной степени определяется качеством изготовления тел качения – роликов. В условиях производства наиболее распространенным методом обработки сферических торцов конических роликов является бесцентровое шлифование периферией круга с непрерывной подачей.
Для образования сферической поверхности ролика на ОАО «ЕПК Волжский» используется, в частности, специальный шлифовальный автомат мод. SXK-5A. Станок обрабатывает ролики с наружным диаметром 6–25 мм и углом конической поверхности 2–8° [6].
Согласно классификации [9], схема базирования относится к способу, когда ролик устанавливается образующей поверхностью по направляющей базе, реализуемой путем контакта ролика с торцовыми поверхностями жестких опорных дисков. Диски установлены соосно и вращаются в противоположные стороны с разной угловой скоростью, обеспечивая вращение заготовки вокруг своей оси и оси круговой подачи. В процессе качения по дискам заготовка вступает в контакт с боковой поверхностью паза направляющего приспособления деталей, соосно установленного с дисками. Скорость подачи базовой поверхности ролика определена в работе [2].
В работах [1; 3; 5; 8] выполнен анализ существующих способов шлифования. Для разработки математической модели формообразования сферы исследована кинематика движения абразивного зерна. С целью обеспечения стабильного параметра «длина ролика» исследовано влияние различных погрешностей, возникающих в процессе шлифования. Приведены результаты испытаний, полученных при шлифовании различными кругами поверхности сферы ролика.
Абразивный инструмент на операции сферошлифования состоит из трех кругов различных характеристик и высоты. Это позволяет в одном проходе ролика через зону обработки соединить черновое, получистовое и чистовое шлифование. Известно, что производительность процесса и качество обработанной поверхности во многом зависят от интенсивности съема припуска. В частности, это убедительно показано на операции глубинного шлифования [4; 7].
На станке SXK-5A удаление заданного припуска обеспечивается в результате смещения центра вращения прижимных дисков и направляющего приспособления с роликами относительно центра правки шлифовального круга.
Цель данной работы заключалась в создании математической модели скорости съема припуска за период движения ролика конического подшипника в зоне шлифования на станке SXK-5A.
Для достижения поставленной цели были решены следующие задачи:
-
определена закономерность изменения величины радиального съема материала и скорости её изменения за период шлифования;
-
исследовано влияние высоты шлифовального круга и радиуса сферической поверхности ролика на съем припуска и скорость его изменения за время шлифования.
Закономерность изменения величины припуска определена исходя из геометрических размеров зоны шлифования без учета характеристики инструмента и размеров обрабатываемой поверхности.
Согласно кинематической схеме станка (рис. 1) для обеспечения снятия припуска ось окружной подачи ролика (ось направляющего приспособления деталей) необходимо смещать на величину [10]:
![]()
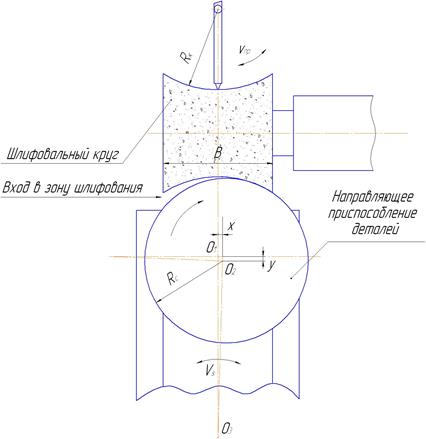
Рис. 1. Схема шлифования и правки на станке SXK-5A:
vпp – возвратно-поступательная скорость подачи правящего инструмента; vs – скорость подачи ролика; Rc – радиус направляющего приспособления деталей.
где Rs – радиус сферического торца ролика; B – высота шлифовального круга; Т – величина снимаемого припуска. Для определения радиуса правки шлифовального круга там же рекомендована следующая формула:

Смещение на величину х обеспечивается поворотом направляющего приспособления вокруг центра О3 (рис. 1). В результате первоначальный центр вращения сепаратора О1 занимает положения О2, т.е. смещается не только по оси абсцисс на величину х, но и по оси ординат на величину у. Так как радиус вращения значительно превышает величину х, смещение у будет не более 0,1 мкм. В связи с малой величиной в дальнейших расчетах смещение у не учитывали.
Кинематическая схема зоны шлифования на станке SXK-5А приведена на рис. 2. Перед тем как войти в зону шлифования, ролик попадает под направляющую пластину, что обеспечивает плавное врезание.
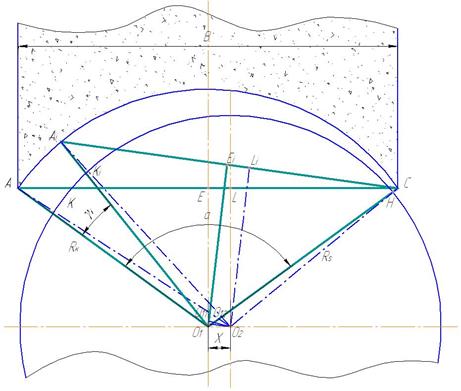
Рис. 2. Схема зоны шлифования станка SXK-5A.
Припуск, снимаемый за период обработки:
![]() ,
,
где АК – расстояние от вершины ролика до опорного диска в момент входа в зону шлифования; СН – расстояние от вершины ролика до опорного диска.
АК находим из формулы:
![]() , (1)
, (1)
где AE=1/2B; ЕL=х; АО1 =Rк.
После подстановки в (1) получаем:
![]() (2)
(2)
В произвольной точке Аi величина снимаемого припуска Тi будет равна:
![]() , (3)
, (3)
где AiKi – расстояние от вершины ролика до опорного диска при некотором угле поворота ролика в зоне шлифования γi.
После преобразований получаем формулу для нахождения AiKi:
![]() , (4)
, (4)
где KiO2= KO2.
Подставив (2) и (4) в (3), получаем величину снимаемого припуска Ti:
![]() , (5)
, (5)
где α - центральный угол, зависящий от высоты шлифовального круга В.
Для определения скорости изменения величины припуска углы (α) и (γ) представим в виде переменных от времени шлифования (τ):
α=τпw=τп360n /60=6nτп и γ= τw=τ360n/60=6nτ,
где n – число оборотов направляющего приспособления деталей; τп – полное время шлифования одного ролика; τ – время прохождения ролика при повороте на угол γi , 0≤τ≤τп.
После подстановки τп и τ в (5), получим:
![]() . (6)
. (6)
Для определения скорости изменения припуска найдем производную от Т по времени τ:
![]() . (7)
. (7)
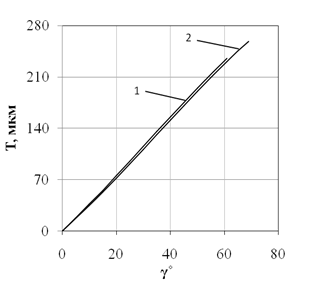
По формулам (6) и (7) для роликов 7305А.04 и У-1027313А.04 рассчитаны значения Т и Q за период шлифования на станке SXK-5A и построены графики зависимостей от угла α (рис. 3а) и от времени τ (рис. 3б).
Исходные данные для расчета: высота шлифовального круга (В) – 140 мм; частота вращения направляющего приспособления деталей (n) – 2 об/мин; радиус сферы ролика (Rs) – 128-10 мм (для ролика У-1027313А.04); 143-10 мм (для ролика 7305А.04).
 а
а 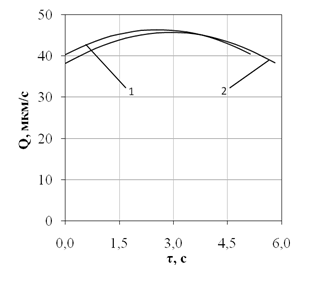 б
б
Рис. 3. Изменение величины удаляемого припуска Т от угла γ (а) и скорости удаления припуска Q от времени шлифования τ (б); 1 - ролик 7305А.04; 2 - ролик У-1027313А.04.
Время обработки зависит от высоты шлифовального круга радиуса сферы ролика, с увеличением которых при прочих равных факторах время обработки возрастает. Для ролика 7305А.04 время шлифования 5,13 с; для ролика У-1027313А.04 – 5,81 с.
Выводы
Разработаны математические модели величины припуска и скорости её изменения за время прохождения роликом зоны шлифования, учитывающие смещение оси вращения роликов в направляющем приспособлении после правки шлифовального круга.
В результате дифференцирования математической модели припуска по времени установлено, что до середины пути ролика в зоне шлифования скорость съема припуска возрастает (на 15% у ролика 7305А.04, на 13% у ролика У-1027313А.04), затем снижается почти до исходных значений.
Для рассмотренных примеров шлифования сферы величина снимаемого припуска изменяется почти пропорционально углу поворота ролика в зоне обработки.
Рецензенты:
Пушкарев О.И., д.т.н., профессор кафедры «Общетехнические дисциплины» Волжского института строительства и технологий (филиал) ФГБОУ ВПО «Волгоградский государственный архитектурно-строительный университет», г. Волгоград;
Санинский В.А., д.т.н., профессор кафедры «Технология и оборудование машиностроительных производств» Волжского политехнического института (филиал) ФГБОУ ВПО «Волгоградский государственный технический университет», г. Волгоград.



