Базой для построения математической модели служат основополагающие принципы теоретической механики и теории механизмов и машин [1–3]. Рабочее оборудование (РО) экскаватора соответствует определению механической системы как совокупности материальных тел, положения и движения которых взаимосвязаны. Удобно представить РО в виде кинематической цепи, состоящей из жестких звеньев, входящих в кинематические пары. Здесь уместна аналогия с конструкциями робототехнических устройств [4, 5]. РО экскаватора, так же, как и оборудование робота, включает в себя несущую механическую систему (НМС) и исполнительную систему (ИС).
НМС обладает расчетной прочностью и жесткостью – это каркас, скелет. Задача ИС – обеспечение определенности движения звеньев НМС. ИС содержит силовые модули, размещенные на звеньях НМС.
НМС экскаватора обратная лопата с гидравлическим приводом показана на рис. 1 в виде кинематической цепи в системе координат Охуz.
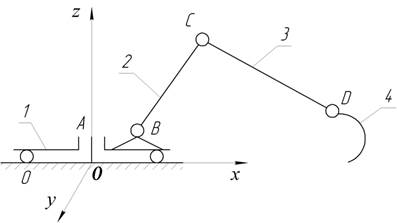
Рис. 1. Несущая механическая система в виде кинематической цепи:
0 – рама экскаватора с механизмом передвижения (стойка); 1 – поворотная платформа; 2 – стрела; 3 – рукоять; 4 – ковш;
А, В, С, D – кинематические пары
Легко подсчитать, что НМС представляет собой кинематическую цепь с четырьмя степенями подвижности. При выполнении операции копания звено 1 заторможено относительно стойки, звенья 2, 3, 4 совершают сложное движение в плоскости Oxz, поэтому число степеней подвижности уменьшается на единицу и становится равным трем.
Для обеспечения определенности движения кинематической цепи по рис. 1 требуются четыре силовых модуля, по числу степеней подвижности (механизм поворота платформы, гидроцилиндры стрелы, рукояти и ковша).
Кинематическая цепь РО в целом включает в себя в качестве звеньев и элементы ИС. Данное обстоятельство приводит к трансформации кинематической цепи по рис. 1 в вид, показанный на рис. 2. Модуль, осуществляющий поворот платформы, не показан.
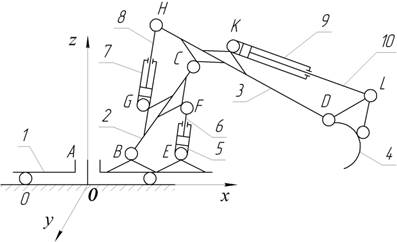
Рис. 2. Рабочее оборудование в виде кинематической цепи:
0 – рама экскаватора; 1 – поворотная платформа; 2 – стрела; 3 – рукоять;
4 – ковш; 5, 6 – гильза и шток гидроцилиндра стрелы; 7, 8 – гильза и шток гидроцилиндра рукояти;
9, 10 – гильза и шток гидроцилиндра ковша;
А, В, С, D, E, F, G, H, K, L – кинематические пары вращения
Модули ИС, ответственные за рабочие движения при копании, представляют собой три гидроцилиндра, каждый из которых входит в кинематическую цепь в виде двух звеньев – гильзы и штока, вместе составляющих пару поступательного движения. Все кинематические пары – пятого класса.
Целесообразно рассмотреть вопрос о правомерности включения гидроцилиндров в кинематическую цепь. По функциональному признаку это двигатели прямолинейного движения, они могут быть представлены в виде дополнительных масс звеньев НМС. Однако с точки зрения конструкции это однозначно пары поступательного перемещения, и в таком качестве их введение в кинематическую цепь вполне обоснованно.
Силы, действующие на кинематическую цепь, разделяются на внешние, приложенные к звеньям со стороны не входящих в состав цепи тел, и внутренние – между звеньями в кинематических парах (реакции связей). Реакции связей представляют собой силы (моменты сил) действия одного звена пары на другое.
В реальных кинематических парах вращательного движения возникают моменты сил трения в шарнирах, в парах поступательного движения – силы трения между ползуном и направляющей. Часто в проектировочных и оценочных расчетах полагают кинематические пары идеальными и силы (моменты сил) трения в них не учитывают. В дальнейшем в общих рассуждениях при упоминании таких силовых факторов, как силы трения (сопротивления) и инерции, используется общий термин сила, при этом момент силы подразумевается.
Особо следует отметить силы, развиваемые модулями ИС. По отношению к кинематической цепи по рис. 1 эти силы внешние, т.к. силовые модули в НМС не входят. Однако после включения модулей в кинематическую цепь их элементы становятся звеньями, как это показано на рис. 2. Поэтому силы, развиваемые рабочей жидкостью в полостях гидроцилиндров и действующие на гильзу и шток как на звенья кинематической пары поступательного движения, в кинематической цепи РО следует отнести уже к категории внутренних сил.
В силовых расчетах механизмов исходной внешней силой является сопротивление объекта воздействия перемещению концевого звена кинематической цепи. Для РО экскаватора такой силой считают силу сопротивления грунта копанию. На стадии проектирования определить ее величину можно только приближенно, ориентируясь на ожидаемые характеристики грунта.
К внешним относятся также силы тяжести звеньев РО. Силы тяжести играют роль движущих, когда при перемещении ковша по заданной траектории центр тяжести РО опускается. В противном случае силы тяжести выступают как силы сопротивления.
Известны два метода динамического расчета систем: метод, основанный на непосредственном решении общих теорем динамики, и метод кинетостатики. Сравнение этих методов будет выполнено ниже; здесь же укажем, что обязательным условием достоверного кинетостатического анализа реальной кинематической цепи является учет сил инерции звеньев.
Очевидно, что не только трудоемкость формирования математической модели, но и сама возможность решения входящих в нее уравнений находятся в непосредственной зависимости от теоретических положений, лежащих в ее основе. Поэтому прежде, чем приступать к составлению модели, следует адекватно оценить предлагаемые теорией методы динамического расчета систем.
Первый из них – метод решения основных уравнений динамики механических систем (обозначим его через МДС). Он создан на базе фундаментальных исследований Л. Эйлера, Ж. Даламбера, Ж. Лагранжа и др. В частности, Ж. Лагранжем разработан общий аналитический способ решения задач динамики на основе принципа возможных перемещений. В числе положений, которыми оперирует МДС, важное место занимает известная теорема о конечном изменении кинетической энергии, которая в общем виде выражается формулой
К – К0 = Ае + Аi (1)
где К0, К – значения кинетической энергии системы в начальном и текущем положениях; Ае, Аi – работа внешних и внутренних сил соответственно.
К внешним силам для кинематической цепи РО, как было показано выше, относятся силы тяжести звеньев и сопротивление грунта, к внутренним – реакции связей. Поскольку связи на данном этапе исследования считаются идеальными, то трение в них не учитывается.
Реакции в шарнирной паре приложены в одной точке, действуют на разные звенья, равны по модулю и противоположно направлены, поэтому их работа равна нулю.
Реакции в поступательных парах – гидроцилиндрах – равны силам давления жидкости и приложены к поршням и гильзам. В процессе движения РО точки приложения реакций в каждой из поступательных пар перемещаются по разным траекториям, причем поршни со штоками смещаются вдоль гильз. Таким образом, эти реакции в k-ой поступательной паре совершают работу, которая на перемещении dsk равна
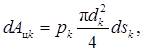 (2)
(2)
где pk – давление в k-ом гидроцилиндре; dk – диаметр k-го гидроцилиндра; dsk – элементарное перемещение штока k-го гидроцилиндра относительно гильзы.
Может возникнуть впечатление, что утверждение о том, что внутренние силы совершают работу, противоречит приведенному выше выводу о равенстве нулю работы реакций в шарнирах. В действительности же это противоречие кажущееся. Следует учесть, что поступательные пары функционально являются двигателями. Силы давления по своей сути относятся к движущим силам, а внутренние они постольку, поскольку одновременно играют роль реакций в парах.
После подстановки выражений работ формула (1) принимает вид
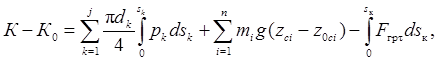 (3)
(3)
где j – число гидроцилиндров; sk – перемещение штока k-го гидроцилиндра относительно гильзы; mi – масса i-го звена; z0ci, zci – начальная и конечная высотные координаты центра тяжести i-го звена; g – ускорение свободного падения; Fгрτ – составляющая силы сопротивления грунта, касательная к траектории движения режущей кромки зуба ковша; sк – перемещение режущей кромки зуба ковша.
Первые два слагаемых в правой части (3) могут быть как положительными, так и отрицательными; третье, очевидно, присутствует при врезании ковша и заполнении его грунтом.
Таким образом, силовые расчеты РО с использованием МДС выполняются по следующему алгоритму:
– в соответствии с видом землеройных работ пооперационно определить траектории движения ковша в трехмерной системе координат;
– по каждой операции цикла установить требуемые значения вектора скорости ковша;
– по геометрическим параметрам траектории и техническому заданию на разработку экскаватора предварительно принять размеры и массы звеньев РО;
– по техническому заданию на разработку экскаватора определить ожидаемые прочностные характеристики наиболее «тяжелого» грунта;
– составить систему уравнений динамики вида (3) в интегральной или дифференциальной форме;
– решить систему относительно первого слагаемого в правой части.
В результате будут получены значения движущих сил в аналитическом виде, что даст возможность:
а) выполнить расчет гидропривода РО;
б) на основе прочностных расчетов уточнить размеры и массы звеньев;
в) провести оптимизацию конструкции РО и экскаватора в целом по заданному критерию.
Вторым методом решения задач динамики систем является метод кинетостатики. Суть его в том, что дифференциальным уравнениям движения системы придается вид уравнений статики: к звеньям кинематической цепи прикладываются силы инерции, после чего считается, что система под действием активных сил и сил инерции находится в равновесии. Для такой системы справедливы уравнения:
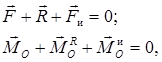 (4)
(4)
где ![]() – главные векторы активных сил, реакций и сил инерции, действующих на систему, соответственно;
– главные векторы активных сил, реакций и сил инерции, действующих на систему, соответственно; ![]() – главные моменты активных сил, реакций и сил инерции относительно выбранного центра (точки О).
– главные моменты активных сил, реакций и сил инерции относительно выбранного центра (точки О).
Порядок практического силового расчета кинематической цепи методом кинетостатики следующий [3]:
– выполняют кинематический анализ системы;
– расчленяют кинематическую цепь на кинематические пары с нулевой степенью подвижности;
– к звеньям каждой кинематической пары прикладывают известные силы активные и инерции;
– из условий равновесия пар находят неизвестные силы, в том числе реакции в кинематических парах.
Силовой анализ методом кинетостатики хорошо зарекомендовал себя в расчетах кинематических цепей с одной степенью подвижности, звенья которых совершают сложное плоское движение. Однако применительно к цепям с бóльшим числом степеней подвижности расчеты серьезно усложняются. Как справедливо указано в [2], метод кинетостатики не имеет никаких преимуществ перед МДС и с развитием современных компьютерных технологий все более уступает место методу аналитической динамики.
Изложенные выше рассуждения приводят к выводу о целесообразности построения математической модели процесса экскавации на базе основных уравнений динамики механических систем.
Общее уравнение динамики дает возможность составлять дифференциальные уравнения движения, не содержащие реакции идеальных связей. Для сравнительно простых систем непосредственное применение этого уравнения вполне оправдано, однако в более сложных случаях использование общего уравнения динамики приводит, как правило, к относительно сложным преобразованиям. Поэтому значительно удобнее пользоваться не общим уравнением динамики, а вытекающими из него уравнениями Лагранжа второго рода, в которых основные преобразования, представляющие наибольшие трудности, проделаны в общем виде.
Рецензенты:
Готлиб Б.М., д.т.н., профессор, заведующий кафедрой «Мехатроника» ФГБОУ ВПО «Уральский государственный университет путей сообщения» Министерства образования и науки Российской Федерации, г. Екатеринбург;
Залазинский А.Г., д.т.н., профессор, заведующий лабораторией системного моделирования, Федеральное государственное бюджетное учреждение науки Институт машиноведения Уральского отделения Российской академии наук, г. Екатеринбург.



