Одной из важнейших задач, относящихся к проблеме поддержания требуемого уровня качества целевого применения ракетно-космических комплексов (РКК), является обоснование решений по управлению техническим состоянием систем телекоммуникационного обеспечения эксплуатации и применения (СТКО ЭП) РКК, позволяющих обеспечить оперативный сбор, обработку и передачу информации о состоянии РКК, принятых решениях по его управлению и результатах реализации управляющих воздействий [1-5].
СТКО ЭП РКК являются сложными техническими системами. В состав СТКО входят многочисленные автоматизированные рабочие места для сбора и обработки информации, аппаратура обработки и передачи сигналов, каналы связи, обеспечивающие системы, здания и сооружения. Вследствие принципа неравнопрочности компонентов сложной технической системы составные части СТКО неравномерно расходуют заложенный при проектировании и изготовлении запас технического ресурса. Кроме того, часть оборудования подвергается моральному старению [5]. Из-за этого в процессе эксплуатации СТКО периодически возникает необходимость обоснования решений о проведении тех или иных мероприятий по восстановлению ресурса составных частей.
Выбор оптимального варианта развития обычно производится с помощью показателей эффективности W, которые определяются как мера достижения цели управления развитием [4,5]. Если таких целей оказывается несколько, то соответствующие задачи называются многокритериальными [4].
На практике крайне редко встречаются случаи, когда один вариант развития или системы превосходит другие по всем выделенным показателям. Возможность получения интегральной оценки каждого варианта развития связана с проблемой шкалирования как количественных, так и качественных показателей, причем среди количественных показателей выделяются такие (например, аппаратурная сложность), которые для различных вариантов развития с большим трудом могут быть выражены в одинаковых единицах измерения. Кроме того, должна быть решена проблема одновременного использования количественных и качественных показателей. Использование теории нечетких множеств [1,2,3] позволяет успешно решить обе эти проблемы.
Цель исследования
Цель исследования заключается в разработке математических моделей определения оптимального варианта развития систем телекоммуникационного обеспечения эксплуатации и применения ракетно-космических комплексов в нечетко заданных условиях.
Исходные предположения и допущения метода исследования
Предлагается общую задачу определения оптимального варианта развития решать в два этапа.
На этапе 1 в качестве процедуры определения множества субоптимальных вариантов целесообразно использовать метод выделения множества недоминируемых альтернативных вариантов развития (АВР) на основе нечетких отношений предпочтения на парах альтернатив [3]. В этом случае по каждому аспекту сравнения в результате опроса экспертов строится нечеткое отношение предпочтения, представляемое в виде матрицы функций принадлежности:
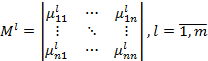 ,
,
где ![]() — количество аспектов сравнения;
— количество аспектов сравнения; ![]() — количество АВР в исходном наборе.
— количество АВР в исходном наборе.
На этапе 2 для выбора лучшего варианта из множества субоптимальных вариантов целесообразно использовать идею метода целевого программирования, которая состоит в отыскании решений, расположенных как можно ближе к вектору одновременно недостижимых целей (идеальной точке) [3]. На этом этапе используются как качественные, так и количественные показатели. В отличие от этапа 1, задаются не нечеткие отношения предпочтения, а нечеткие подмножества на множестве субоптимальных вариантов ![]() по терминологии Кофмана [2], т.е. задается набор функций принадлежности, определенных непосредственно на
по терминологии Кофмана [2], т.е. задается набор функций принадлежности, определенных непосредственно на ![]() , а не на парах альтернатив.
, а не на парах альтернатив.
Постановка задачи исследований
Математически постановка задачи исследования представляется в следующем виде.
Этап 1. Заданы: набор альтернативных вариантов ![]() ; множество аспектов сравнения
; множество аспектов сравнения ![]() ; вектор нечетких отношений предпочтения
; вектор нечетких отношений предпочтения ![]() , где
, где ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Требуется определить множество субоптимальных вариантов ![]() , где
, где ![]() — знак нестрогого нечеткого предпочтения на множестве аспектов сравнения.
— знак нестрогого нечеткого предпочтения на множестве аспектов сравнения.
Этап 2. Заданы: множество субоптимальных вариантов ![]() ; множество показателей эффективности
; множество показателей эффективности ![]() , причем
, причем![]() — количественные;
— количественные; ![]() — качественные; значения показателей
— качественные; значения показателей![]() и их допустимые диапазоны изменения
и их допустимые диапазоны изменения ![]() , (
, (![]() ); количество уровней градаций
); количество уровней градаций ![]() по каждому показателю
по каждому показателю ![]() , (
, (![]() ).
).
Требуется определить оптимальный вариант ![]() , для которого выполняется условие
, для которого выполняется условие ![]() , где
, где![]() — знак строгого предпочтения по множеству показателей
— знак строгого предпочтения по множеству показателей ![]() .
.
Разработка математических моделей выбора оптимального варианта
Рассмотрим первоначально вопрос определения множества субоптимальных вариантов при наличии одного нечеткого отношения предпочтения (НОП). В этом случае поставленная на этапе 1 задача представляется парой <![]() >, где
>, где ![]() — множество АВР, a
— множество АВР, a ![]() — нечеткое отношение предпочтения, определяемое как нечеткое подмножество декартова произведения
— нечеткое отношение предпочтения, определяемое как нечеткое подмножество декартова произведения ![]() , характеризующееся такой функцией принадлежности
, характеризующееся такой функцией принадлежности ![]() , что
, что ![]() , причем
, причем ![]() принимается как субъективная мера выполнения отношения
принимается как субъективная мера выполнения отношения ![]() . Иначе:
. Иначе: ![]() , где
, где ![]() .
.
Каждому ![]() соответствует строгое НОП
соответствует строгое НОП![]() , функция принадлежности которого определяется по формуле:
, функция принадлежности которого определяется по формуле:
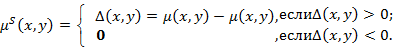 (1)
(1)
Очевидно, что для любых АВР![]() величина
величина ![]() есть степень, с которой АВР у доминируется АВР х.
есть степень, с которой АВР у доминируется АВР х.
При фиксированном ![]() функцию
функцию ![]() можно рассматривать как функцию принадлежности нечеткого множества всех АВР х, которая строго доминируется АВР у. Отсюда следует, что множество всех АВР х, которые не доминируются альтернативой у, представляет собой дополнение в х введенного множества
можно рассматривать как функцию принадлежности нечеткого множества всех АВР х, которая строго доминируется АВР у. Отсюда следует, что множество всех АВР х, которые не доминируются альтернативой у, представляет собой дополнение в х введенного множества ![]() . Следовательно, это новое нечеткое множество описывается функцией принадлежности вида:
. Следовательно, это новое нечеткое множество описывается функцией принадлежности вида:
![]() ,
,![]() . (2)
. (2)
Отсюда следует, что для выделения в X подмножества всех АВР, каждая из которых не доминируется ни одной АВР из X, необходимо взять пересечение нечетких подмножеств (2) по всем ![]() . Такое пересечение может быть определено как нечеткое множество недоминируемых АВР, функция принадлежности
. Такое пересечение может быть определено как нечеткое множество недоминируемых АВР, функция принадлежности ![]() которой определяется согласно правилам нахождения пересечения нечетких множеств:
которой определяется согласно правилам нахождения пересечения нечетких множеств:![]() =
= ![]()
или ![]() =
= ![]() . (3)
. (3)
Согласно (3) ![]() представляет собой степень, с которой АВР не доминируется ни одной из АВР множества Х.
представляет собой степень, с которой АВР не доминируется ни одной из АВР множества Х.
В [3] на основе (1) вводится также множество четко недоминированных решений (в данном случае – АВР) в виде:
![]() =
= ![]() . (4)
. (4)
Альтернативный вариант![]() будем называть максимальным в X в соответствии с НОП Р, если не существует такого
будем называть максимальным в X в соответствии с НОП Р, если не существует такого ![]() , включая само х, для которого выполнялось бы условие
, включая само х, для которого выполнялось бы условие ![]() , что соответствует
, что соответствует ![]() > 0.
> 0.
Понятие множества Парето впервые было сформулировано для многокритериальных задач принятия решений, или, что то же самое, для многих отношений предпочтения. Для нечетких задач принятия решения множество Парето вводится и для случая одного НОП. При этом оно определяется как множество всех максимальных элементов в X по отношению Р и обозначается ![]() .
.
В [1] доказываются следующие утверждения:
1. ![]() =
= ![]() .
.
2. Если X конечно, а Р транзитивно, то![]() и внешне устойчиво.
и внешне устойчиво.
Под свойствами транзитивности НОП Р понимается выполнение условия:
![]() ,
,![]() ,
, ![]() . (5)
. (5)
Иначе: если х предпочтительнее z, az предпочтительнее у, то условие транзитивности выполнено при предпочтительности х перед у.
Внешне устойчивым является также подмножество![]() , если для любого
, если для любого
![]() найдется такое
найдется такое ![]() , что выполняется условие
, что выполняется условие![]() .
.
Однако главной целью является получение множества Парето или его аналога для нечетких многокритериальных задач. Формулы (2) и (3) не могут быть использованы для этой цели.
В [1] предлагается следующий подход.
1. Определяется понятие четкого отношения предпочтения, которое является согласованным с нечетким отношением предпочтения Р на одном и том же множестве альтернативных вариантов.
2. Доказывается, что множество Парето такого четкого отношения и множество четко недоминируемых альтернатив отношения Р совпадают.
3. Вводится четкое отношение предпочтения F, соответствующее конкретному НОП Р в следующем виде:
![]() . (6)
. (6)
4. Доказывается, что F согласовано с Р и, следовательно,
![]() =
= ![]() . (7)
. (7)
Рассмотрим нечеткую многокритериальную задачу принятия решений. Такая задача представляется парой <X, P>, где
![]() ,
, ![]() ;
;![]() .
.
В этом случае Р является векторным нечетким отношением предпочтения (ВНОП). Его компонентами являются обычные (одномерные или скалярные) отношения предпочтения, рассмотренные выше. Множество Парето в этом случае выражается через множество четко недоминируемых альтернатив по всему вектору![]() .
.
Каждому ![]() ,
,![]() соответствует согласованное с ним четкое отношение предпочтения
соответствует согласованное с ним четкое отношение предпочтения ![]() в соответствии с формулой (7). Тогда на основе вектора Р с нечеткими компонентами можно сформировать некоторое четкое векторное отношение предпочтения в виде:
в соответствии с формулой (7). Тогда на основе вектора Р с нечеткими компонентами можно сформировать некоторое четкое векторное отношение предпочтения в виде: ![]() , для которого обычными способами определяются Парето-доминирование
, для которого обычными способами определяются Парето-доминирование ![]() и соответствующее множество Парето
и соответствующее множество Парето ![]() . Соответственно
. Соответственно ![]() . В [4] показано, что если все компоненты вектора Р транзитивны, а X — конечно, то
. В [4] показано, что если все компоненты вектора Р транзитивны, а X — конечно, то ![]() и внешне устойчиво.
и внешне устойчиво.
Если имеется m показателей (аспектов, критериев) сравнения АВР, то отношения четкого предпочтения F могут быть представлены с помощью m матриц смежности
![]() ,
, ![]() . Каждая строка и столбец такой матрицы соответствуют некоторому
. Каждая строка и столбец такой матрицы соответствуют некоторому
АВР, а элемент матрицы 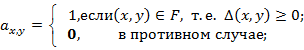 .
.
Множество Парето ![]() определится как совокупность некоторого количества АВР, для которых все элементы соответствующих им строк во всех матрицах
определится как совокупность некоторого количества АВР, для которых все элементы соответствующих им строк во всех матрицах ![]() ,
,![]() равны 1.
равны 1.
Результаты исследования и их обсуждение
Обеспечить транзитивность всех компонент вектора Р удается далеко не во всех случаях, так как соблюдение условия (5) требует выполнения особых правил получения функций принадлежности нечетких отношений предпочтения. В связи с этим в общем случае четкое множество Парето ![]() может быть пусто. При
может быть пусто. При ![]() для определения множества субоптимальных вариантов предлагается использовать понятие r-недоминируемых альтернатив и нечеткого множества Парето. Последовательность действий при этом сводится к следующему.
для определения множества субоптимальных вариантов предлагается использовать понятие r-недоминируемых альтернатив и нечеткого множества Парето. Последовательность действий при этом сводится к следующему.
1. С помощью линейной свертки
![]() , (8)
, (8)
где ![]() – коэффициент важности частных показателей сравнения
– коэффициент важности частных показателей сравнения
![]() ; m — количество частных показателей сравнения; осуществляется переход от векторного к скалярному НОП.
; m — количество частных показателей сравнения; осуществляется переход от векторного к скалярному НОП.
2. Аналогично формулам (1), (7) определяется![]() и
и![]()
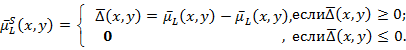 (9)
(9)
![]() . (10)
. (10)
Очевидно, что ![]() является по-прежнему функцией принадлежности альтернативы х множеству альтернатив, не доминируемых ни одним
является по-прежнему функцией принадлежности альтернативы х множеству альтернатив, не доминируемых ни одним![]() , но уже в соответствии с новым «свернутым» по формуле (8) НОП. Если
, но уже в соответствии с новым «свернутым» по формуле (8) НОП. Если ![]() для некоторой альтернативы
для некоторой альтернативы ![]() , тогда
, тогда ![]() может доминироваться другими АВР со степенью (1–r).
может доминироваться другими АВР со степенью (1–r).
3. Вводятся нечеткое множество Парето ![]() и множество r-недоминируемых альтернатив
и множество r-недоминируемых альтернатив![]() :
:
![]() ;
; ![]() , (11)
, (11)
где 0 ≤ r ≤ 1.
Если ![]() = Ø, то все множество АВР находится между гипотетическими границами множеств
= Ø, то все множество АВР находится между гипотетическими границами множеств ![]() и
и ![]() [1].
[1].
4. Начиная с r = 1, через заданный интервал осуществляется понижение порога (уровня) доминирования до тех пор, пока очередное множество r-недоминируемых АВР не будет иметь мощность не более некоторой заранее определенной величины.
При решении задачи, поставленной на этапе 2, сделаем предположение, что все используемые на этом этапе показатели положительно ориентированы.
Введем нечеткое множество ![]() — «оптимальные варианты» по показателю
— «оптимальные варианты» по показателю ![]() ,
,
![]() . Тогда для каждого АВР
. Тогда для каждого АВР ![]() ,
, ![]() (K — мощность множества субоптимальных вариантов
(K — мощность множества субоптимальных вариантов![]() ) по каждому показателю
) по каждому показателю ![]() ,
,![]() , величина
, величина ![]() определяется как функция принадлежности альтернативы
определяется как функция принадлежности альтернативы ![]() нечеткому множеству
нечеткому множеству ![]() .
.
Значения оценок количественных показателей, получаемые для каждого субоптимального варианта с помощью имитационного моделирования на ЭВМ, могут быть нечеткими. «Размытость» количественных показателей при этом связана с корректностью реализуемых моделью зависимостей и точностью моделирования. Согласно [2] функция принадлежности для количественного показателя в этом случае может быть задана в виде:
![]() , (12)
, (12)
где ![]() — диапазон изменения i-го показателя,
— диапазон изменения i-го показателя, ![]() — нижний (в смысле худший) предел диапазона изменения i-го показателя. Для каждого АВР может быть получен набор функций принадлежности
— нижний (в смысле худший) предел диапазона изменения i-го показателя. Для каждого АВР может быть получен набор функций принадлежности ![]() ,
,![]() .
.
Дальнейшее использование ![]() связано с употреблением в том или ином виде свертки набора функций принадлежности:
связано с употреблением в том или ином виде свертки набора функций принадлежности:
![]() ;
; ![]() , (13)
, (13)
где коэффициент ![]() — важность i-го показателя качества, определяемый экспертным способом (0 £
— важность i-го показателя качества, определяемый экспертным способом (0 £ ![]() £ 1).
£ 1).
Как правило, ![]() = const при изменении
= const при изменении![]() внутри диапазона
внутри диапазона ![]() , что соответствует линейной зависимости
, что соответствует линейной зависимости ![]() . Однако приращение показателя
. Однако приращение показателя ![]() имеет большую важность в верхней части диапазона
имеет большую важность в верхней части диапазона ![]() , чем в нижней (пример — приращение вероятности безотказной работы устройства). Для введения нелинейной зависимости
, чем в нижней (пример — приращение вероятности безотказной работы устройства). Для введения нелинейной зависимости ![]() целесообразно диапазон изменения показателя
целесообразно диапазон изменения показателя ![]() разделить на некоторое число поддиапазонов
разделить на некоторое число поддиапазонов ![]() величиной
величиной ![]() :
: ![]() и для каждого
и для каждого![]() -го поддиапазона задать коэффициент важности
-го поддиапазона задать коэффициент важности ![]() при условии нормировки
при условии нормировки ![]() . Тогда функция принадлежности АВР
. Тогда функция принадлежности АВР ![]() по i-му нечеткому количественному показателю, имеющему значение
по i-му нечеткому количественному показателю, имеющему значение ![]() и относящемуся к
и относящемуся к ![]() -му поддиапазону, определяется следующим образом:
-му поддиапазону, определяется следующим образом: ![]() , где
, где ![]() определяется из (12). В этом случае (13) представляется в виде:
определяется из (12). В этом случае (13) представляется в виде:
![]() , где
, где![]() выбирается из множества
выбирается из множества![]() в соответствии с условиями: (
в соответствии с условиями: (![]() )
)![]() ;
;![]() ;
;![]() .
.
Выводы
В статье описывается использование двухэтапной процедуры выбора оптимального варианта развития систем телекоммуникационного обеспечения эксплуатации ракетно-космических комплексов в нечетко заданных условиях. На первом этапе из заданного набора вариантов выделяется множество лучших по заданным критериям вариантов (субоптимальных вариантов). На втором — определяется (с использованием имитационного моделирования или аналитических зависимостей) лучший вариант из множества субоптимальных вариантов, называемый оптимальным.
Рецензенты:
Козлов В.В., д.т.н., профессор, профессор кафедры ФГКВОУ ВПО «Военно-космическая академия имени А.Ф. Можайского» Министерства обороны РФ, г. Санкт-Петербург;
Смагин В.А., д.т.н. профессор, профессор кафедры ФГКВОУ ВПО «Военно-космическая академия имени А.Ф. Можайского» Министерства обороны РФ, г. Санкт-Петербург.



