В современных условиях развития экономики, производственной сферы и наукоемких технологий к инженерам предъявляются новые требования, сформулированные в ФГОС ВО по направлению подготовки бакалавров «Технология лесозаготовительных и деревоперерабатывающих производств» в виде комплекса компетенций, среди которых выделяются компетенции, связанные с исследовательской деятельностью инженера, с его способностью применять математические знания и методы при решении инженерных задач, что обуславливает вовлечение студента в подобную деятельность. Однако в настоящее время наблюдается противоречие между предъявляемыми требованиями к бакалавру-инженеру, заключающееся в необходимости применения математических знаний и методов в профессиональной деятельности, и недостатком получения опыта подобной деятельности в вузе. Разрешение этого противоречия возможно при выполнении организационно-педагогических условий, направленных на формирование исследовательской деятельности студентов после завершения освоения основного курса математики, в рамках поликонтекстного образовательного модуля «Математика в лесоинженерном деле» [3, 5].
Цель настоящей статьи заключается в описании методических возможностей формирования исследовательской деятельности бакалавров лесоинженерного дела в условиях поликонтекстного образовательного модуля «Математика в лесоинженерном деле».
Описывая методику формирования исследовательской деятельности студентов остановимся на ее целевом, содержательном, организационном и оценочном компонентах. Цели формирования исследовательской деятельности студента в процессе математической подготовки ориентированы на личностное развитие, профессиональное самоопределение и карьерный рост, направлены на усвоение знаний, умений, навыков и способов математической деятельности, перенос их во вне предметную область, формирование способности к самостоятельному проведению исследования [5]. Содержание образовательного модуля ориентировано на междисциплинарность, на будущую профессиональную деятельность, на их интеграцию. В основу поликонтекстного содержания образовательного модуля положена теория контекстного обучения [2], направленная на постепенное вовлечение студента в профессиональную деятельность. Используя опыт других авторов в определении принципов проектирования содержания междисциплинарного образовательного модуля [6] и учитывая требования нормативных документов, мы сформулировали принципы формирования содержания образовательного модуля «Математика в лесоинженерном деле»:
- реализация практико-ориентированного, междисциплинарного и профессионального контекстов;
- принцип доступности (студентам предлагается содержание, соответствующее курсу обучения);
- принцип дифференцируемости (ориентация на студентов различного уровня подготовки).
Основным средством достижения обозначенных целей являются математические задачи с практико-ориентированным, междисциплинарным и профессионально-ориентированным контекстами исследовательской направленности, образующие специальный комплекс задач. Среди предложенных задач встречаются как задачи, направленные на формирование отдельных компонент исследовательской деятельности, так и задачи, требующие комплексного исследования, результат решения которых может быть оформлен студентом в виде статьи.
Рассмотрим пример поэтапного решения математической задачи исследовательской направленности с контекстом деревообработки. Представленная задача способствует вовлечению студента в исследовательскую деятельность и направлена на формирование ее основных элементов. В задаче отражено профессиональное содержание, необходимо применить известные знания и методы в новой ситуации, но проводимые вычисления не являются громоздкими. Преподаватель при решении этой задачи подчеркивает ее актуальность и выполняет консультирующую функцию.
Задача: из круглого бревна определенного диаметра требуется вырезать стойку прямоугольного сечения таким образом, чтобы она могла воспринимать наибольшую нагрузку. Какими должны быть размеры сечения [4].
1. Организационно-мотивационный этап. На этом этапе студенты высказывают свои предположения о важности подобных расчетов. Определяются с понятием «стойка прямоугольного сечения». Здесь акцентируется востребованность деревянных стоек и колонн при малоэтажном строительстве, актуальность просчета несущих конструкций.
2. Этап постановки проблемы. Проблема заключается в определении размеров стойки для восприятия максимальной нагрузки.
3. Этап сбора фактического материала, его систематизации и анализа. Стойка является элементом конструкции, работающим на сжатие, значит, наибольшая нагрузка воспринимается в случае наибольшей площади поперечного сечения. Необходимо обозначить известные величины. Диаметр обозначается за d. Для нахождения наибольшего значения необходимо выразить наибольшую величину.
4. Этап формулирования гипотезы. Если площадь сечения прямоугольника выразить как функцию от сторон и исследовать ее на наибольшее значение, то прямоугольник наибольшей площади, который можно вписать в круг заданного диаметра будет найден, т. е. будут найдены размеры стойки.
5. Проверочный этап. На проверочном этапе студенты производят необходимые расчеты. Нужно длину одной стороны прямоугольника обозначить через x и выразить вторую, используя диаметр. Тогда площадь прямоугольника равна ![]() . Далее требуется найти производную функции
. Далее требуется найти производную функции ![]() , приравнять производную к нулю, решить полученное уравнение и записать корни.
, приравнять производную к нулю, решить полученное уравнение и записать корни.
6. Этап формулирования выводов. На этом этапе дается ответ на вопрос задачи. Так как x – длина, то критической точкой является положительное значение. Необходимо обосновать, что при найденном x функция S(x) достигает максимума. Функция достигает максимума, т. е. площадь максимальная в случае, когда стороны равны. А значит, стойка воспринимает наибольшую нагрузку, когда ее поперечное сечение квадрат. Студент должен проверить, что полученный результат имеет смысл для конкретной задачи и подробно оформить решение.
7. Рефлексивный этап. Проверяется выполнение всех вычислений, оценивается возможность применения метода для решения других задач.
Остановимся на компонентах исследовательской деятельности, формируемых при решении предложенной задачи. Профессионально-ориентированный контекст задачи повышает интерес к ее постановке и решению, способствует пониманию значимости исследовательской деятельности для будущей профессиональной деятельности, ориентирован на усвоение предметных знаний в процессе решения задачи. Процесс поэтапного решения предложенной задачи ориентирован на приобретение студентами опыта в формулировании цели исследования, постановке проблемы, выдвижении гипотезы и ее проверке, выборе метода решения, анализа полученных результатов и их обоснования. На рефлексивном этапе решения предложенной задачи формируются такие компоненты исследовательской деятельности как самоконтроль и оценка своей деятельности. Мы различаем три уровня сформированности выделенных компонент исследовательской деятельности: репродуктивный, эвристический и творческий. В основу выделенных уровней сформированности деятельности студентов положен подход В.П. Беспалько, который выделяет четыре уровня, исходя из степени самостоятельности обучающегося в процессе решения задачи [1, с. 55].
Среди методов формирования исследовательской деятельности, в том числе и в процессе решения исследовательских задач и представления результатов, в условиях образовательного модуля основными являются активные и интерактивные методы, ориентированные на обучение в деятельности, на взаимодействие студентов и преподавателя, на контекст: деловая игра, метод «мозгового штурма», «круглого стола», научно-исследовательского семинара и другие. Одним из ключевых организационных моментов в процессе освоения образовательного модуля является ориентация студента в предложенной теме. На лекции – беседе, лекции – дискуссии, лекции с заранее запланированными ошибками обозначается контекст, в котором применяются математические знания, происходит их актуализация для других дисциплин, ставится проблема. Подобные лекции ориентируют студента на дальнейшее исследование. На лекции-конференции студенты представляют достигнутые результаты, обсуждают их, обмениваются опытом.
При формировании исследовательской деятельности велико значение самостоятельной работы. Как показывает анализ рабочих программ, более 60% из запланированного рабочего времени отводится на самостоятельную работу. В процессе самостоятельной работы студенты находят решение исследовательской задачи, используют для этого прикладные компьютерные программы. Организация самостоятельной работы студентов зависит от их личностных качеств, уровня предметных знаний, от готовности к проведению исследования. Самостоятельная работа студентов может быть индивидуальной – в этом случае студент полностью сам выполняет исследование. Самостоятельная работа с консультантом, в случае если уровень подготовки студента недостаточен для самостоятельного проведения исследования. Групповая самостоятельная работа студентов по решению поставленной задачи применяется в случае объемной задачи, которую можно разбить на несколько более узких задач, а также в случае недостаточного уровня подготовки студентов к исследовательской деятельности.
Реализация поликонтекстного образовательного модуля «Математика в лесоинженерном деле» способствует повышению уровня сформированности исследовательской деятельности студентов в процессе математической подготовки, что подтверждается проводимой диагностикой. При диагностике учитывалась самооценка студентов, экспертная оценка, результаты самостоятельной работы, в которую были включены математические софизмы, математические и прикладные задачи исследовательской направленности, решение которых основано на применении математических знаний в новой предметной области. На рисунках 1 и 2 представлены данные стартовой диагностики и диагностики уровня сформированности исследовательской деятельности студентов «на выходе».
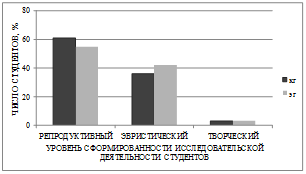
Рис. 1. Уровень сформированности исследовательской деятельности студентов «на входе»
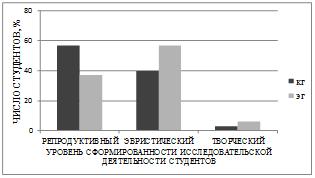
Рис. 2. Уровень сформированности исследовательской деятельности студентов «на выходе»
В экспериментальной группе при изучении основного курса математики студентам предлагались математические задачи исследовательской направленности, поэтому здесь перед освоением образовательного модуля эвристический уровень сформированности исследовательской деятельности несколько выше. При диагностике на завершающем этапе получены следующие результаты: в экспериментальной группе – это студенты, продолжившие математическую подготовку в рамках образовательного модуля «Математика в лесоинженерном деле», эвристический уровень сформированности исследовательской деятельности повысился на 15%, творческий на 3%, в то время как в контрольной группе соотношение уровней существенно не изменилось.
Формирование исследовательской деятельности средствами образовательного модуля осуществляется в условиях актуализации и ориентировании студентов в проблеме на лекции, самостоятельном поиске необходимых знаний и исследовании поставленных задач, обсуждении затруднений в рамках семинарских занятий, представлении результатов на лекции-конференции. Предлагаемая методика, основанная на использования математических задач с различными контекстами исследовательской направленности в рамках образовательного модуля, ориентирована на личностную заинтересованность студента, направлена на его самостоятельность и активность, повышает качество математической подготовки, способствует формированию исследовательской деятельности студентов, его готовности к применению математических знаний и методов в новых условиях, в том числе и при решении профессиональных задач.
Рецензенты:
Шершнева В.А., д.п.н., доцент, профессор кафедры прикладной математики и компьютерной безопасности Института космических и информационных технологий, Сибирский федеральный университет, г. Красноярск;
Шкерина Л.В., д.п.н., профессор, заведующий кафедрой математического анализа и методики обучения математике в вузе, Красноярский государственный педагогический университет им. В.П. Астафьева, г. Красноярск.



