В настоящее время значительное внимание уделяется проблеме применения вибрации при обработке почвы, являющейся наиболее энергоемкой операцией сельскохозяйственного производства. Внимание вызвано главным образом тем, что использование конструкций с колеблющимися рабочими органами позволяет снизить тяговое сопротивление. Вместе с тем, применение конструкций способных обеспечить оптимальный режим колебаний упругого рабочего органа на разных по физико-механическим свойствам почвах является достаточно актуальной проблемой.
Для решения данной проблемы предложена конструкция рабочего органа культиватора [2, 5] С-образная стойка которого выполнена в виде гибкого трубчатого элемента, представляющего собой герметичную трубу некруглого поперечного сечения (см. рис. 1).
Принцип действия рабочего органа заключается в следующем. При подаче давления в полость стойки 2 через штуцер 3 рабочей жидкости либо воздуха происходит деформация сечения, в результате этого её свободный конец с рыхлительной лапой 1 совершает перемещение. При подаче пульсирующего давления рыхлительная лапа совершает колебательные движения с определенной амплитудой и частотой, которые зависят от параметров подаваемого давления. Изменяя параметры давления, можно задать различные режимы колебания, что позволит снизить тяговое сопротивление.
Цель исследования
Целью работы является обоснование параметров рабочего органа культиватора со стойкой в виде гибкого трубчатого элемента, обеспечивающего снижение тягового сопротивления и повышение качественных показателей обработки почвы.
Для решения задач проектирования рабочего органа со стойками в виде гибкого трубчатого элемента необходима математическая модель взаимодействия рабочего органа с почвой, которая с наименьшими временными затратами и с приемлемой для инженерной практики точностью позволит оптимизировать параметры рабочего органа с учетом различных факторов.
Метод исследования
Действие внутреннего давления р проявляется в том, что свободный конец полой стойки, в месте крепления рыхлительной лапы, совершает перемещение. Величина изгибающего момента, возникающего в сечении стойки, пропорциональна величине давления р и может быть определена на основании полубезмоментной теории оболочек [3]. Поэтому задача об определении перемещения стойки под действием давления эквивалентна задаче перемещения трубки под действием момента, приложенного к ее свободному концу. Таким образом, внутреннее давление р входит в уравнения движения (1) посредством изгибающего момента fм.
Стойка представляет собой трубку постоянного плоскоовального либо эллиптического сечения, изогнутую по дуге окружности, один конец которой жестко закреплен, а другой свободен, рис. 1. На свободном конце закреплена рыхлительная лапа массой m1.
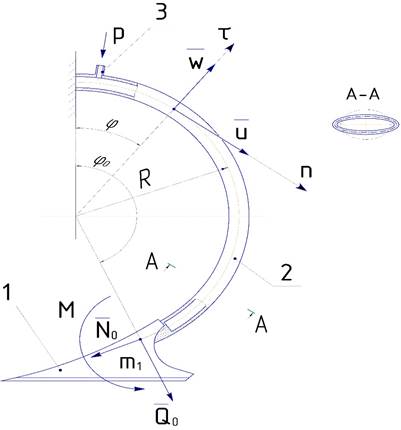
Рис. 1. Расчетная схема рабочего органа культиватора со стойкой в виде гибкого трубчатого элемента: 1 – рыхлительная лапа; 2 – стойка; 3 – штуцер
Внутри трубки может создаваться переменное давление p(t). Давление p(t) вызывает изменение кривизны от трубки и, следовательно, перемещение её свободного конца. Кроме того, на груз, то есть на конец трубки, может действовать осевая сила N и поперечная Q, направленные по касательной и по нормали к оси стержня, а также момент M, рис. 1.
Длина трубки во много раз превосходит размеры поперечного сечения, поэтому трубку будем рассматривать как стержень, изогнутый по дуге окружности радиуса R. Масса груза m1 значительно больше массы трубки m0.
Уравнение движения стержня можно получить из уравнения равновесия В.В. Новожилова с помощью принципа Даламбера [4].
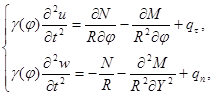(1)
N=
,
, 
. (2)
Граничные условия в точке φ=0:
u(0,t)=0, w(0,t)=0, 
. (3)
В точке φ = φ 0:
. (4)
Начальные условия запишем в виде:
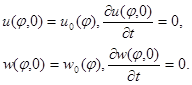(5)
В этих уравнениях:u(
,t), w(,t) – перемещения точки оси стержня с координатой φ;N(,t),Q(,t) – осевая и поперечная (перерезывающая) сила; M(,t) – изгибающий момент в сечении ;
– осевая жесткость трубки; 
– изгибная жесткость трубки; E – модуль упругости материала трубки; 
– погонная масса трубки;
и 
– осевая и нормальное распределение нагрузки на стержень, они могут зависеть от φ,t, u, w, p,
причем зависимость в общем случае может быть нелинейной и достаточно сложной;
– силы, приложенные к рыхлительной лапе и действующие со стороны почвы, они также могут зависеть от φ, t, u, w, p, и от физико-механических свойств почвы[1].
Кроме того, на решение также влияет масса лапыm1, которая непосредственно не входит в уравнения (1) – (5). Для учета массы лапы будем считать погонную массу трубки, перемещенной по длине. При численном решении задачи это более простой вариант. Поэтому приближенно систему можно рассматривать как материальную точку, на которую действуют силы упругости со стороны стержня и внешние силы 
.
Распределенные нагрузки 
и действуют на небольшую часть стойки и значительно меньше по величине, чем силы 
и 
, или будем пренебрегать. Рассмотрим движение точки только в плоскости кривизны трубчатого элемента, поэтому точка имеет две степени свободы uи w.
Для решения динамической задачи для материальной точки необходимо определить зависимость сил упругости, действующих на точку от её перемещений. Так как массой стержня и распределенными нагрузками и пренебрегаем, то уравнения (1) примут вид:
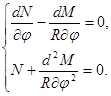(6)
Граничные условия при =0:
u=w=w’=0. (7)
При =0,будем считать заданными перемещения и угол поворота 
:
(8)
Продифференцируем первое уравнение (6)по и сложим со вторым:
.
Общее решение этого уравнения:
(9)
Из (5) и (6,1) находим:
(10)
Из (10) находим
.
Отсюда
. (11)
Из полученных соотношений (9), (10), (11)выразим 
черезN, Q и M:
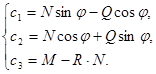(12)
Определим перемещения из (5) имеем:
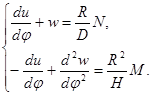(13)
Складываем почленно:
.
В реальных задачах безразмерная величина
. (14)
Будем пренебрегать этой величиной по сравнению с 
. Такое допущение эквивалентно предположению, что осевая жесткость D бесконечно большая величина, то есть ось трубки в процессе деформации не удлиняется.
Итак, получим:
.
Общее решение этого уравнения может быть представлено в виде суммы общего решения однородного и частного решения неоднородного уравнений:
. (15)
Найдем еще производную:
. (16)
Из (13) находим
.
Подставляем сюда выражения (9) и (15) и интегрируем:
. (17)
С помощью граничных условий (7)выразим неопределенные коэффициенты 
через 
Подставляем в (17), (15) и (16) =0, получим:
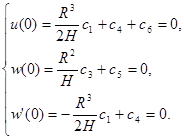
Отсюда находим:
, 
, 
.
Учитывая еще выражения (12) получим:
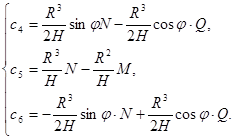(18)
Подставляем в (17) и (15) полученные зависимости (18) и (12), получим выражение для перемещений через усилияN, Q и M:
(19)
Если подставить =0, то получим перемещения груза 
и
в зависимости от сил 
и момента
, приложенных к концу стержня.
Запишем (19) в виде:
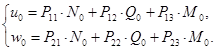
Здесь
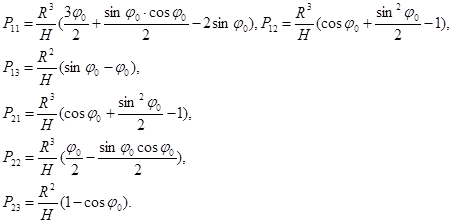(20)
Выразим 
через
:
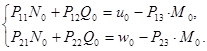
Решаем эту систему по формулам Крамера:
Получим:
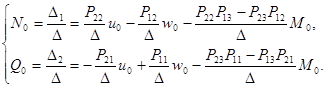
Обозначим:
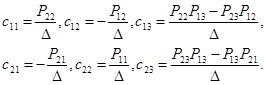(21)
Тогда:
(22)
В этих выражениях: N0 и Q0 – силы, действующие на пружину со стороны лапы; u0 и w0 – перемещения конца стойки, М0 – момент, действующий на стойку.
Момент М0. может создаваться внутренним давлением p, вызывающим изменение кривизны стойки. При определении перемещений конца стойки предполагается, что момент во всех сечениях одинаков, поэтому его можно считать приложенным к концу стойки и равным М0.
Для составления дифференциальных уравнений движения лапы необходимо знать действующие на него силы. Со стороны пружины на лапу действуют силы 
и
направленные в противоположные стороны по отношению к силам 
и 
. Кроме того, на него действуют внешние силы 
и 
, заданные в граничных условиях (4).
Запишем дифференциальные уравнения движения лапы в системе координат с осями 
и
, (рис. 1.)
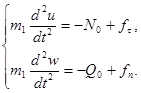
Подставляем сюда выражения для и из (22):
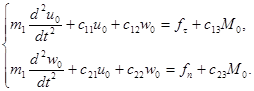(23)
Величины 
– постоянные, определяются из (20), (21), силы и могут зависеть от 
и от других параметров, причем эта зависимость может быть нелинейной и сложной.
Уравнения движения (23) являются системой обыкновенных дифференциальных уравнений. Общее решение для произвольной правой части получить невозможно, но для некоторых частных случаев аналитическое решение можно получить.
Таким образом, получена математическая модель активного рабочего органа культиватора со стойкой в виде гибкого трубчатого элемента, позволяющая учитывать действие пульсирующего давления и силовых факторов со стороны почвы.
Рецензенты:
Чумаков В.Г., д.т.н., доцент, заведующий кафедрой тракторов и сельскохозяйственных машин ФГБОУ ВПО «Курганская государственная сельскохозяйственная академия имени Т.С. Мальцева», Курганская область, с. Лесниково;
Фоминых А.В., д.т.н., профессор, заведующий кафедрой механизацииживотноводства ФГБОУ ВПО «Курганская государственная сельскохозяйственная академия имени Т.С. Мальцева», Курганская область, с. Лесниково.