Анализ и синтез сложных систем непосредственно связан с решением известных прямых и обратных задач. В прямой задаче предполагается определение с помощью операторного уравнения выходной координаты по известному возмущению, известным характеристикам помехи, оператору системы или ее звеньев (рис.1):
;
– управляющий сигнал, 
– выходная координата (реакция на управляющий сигнал), 
– оператор объекта управления.
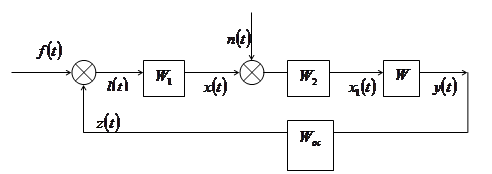
Рис.1. Система с возмущениями и помехами
С учетом взаимодействия управляющего сигнала и помехи:
.
Так что
.
В системах с обратной связью управляющий сигнал 
формируется по сигналу обратной связи 
и возмущению 
, действующему на входе системы:
.
Таким образом, здесь
.
Две обратные задачи связаны с использованием реализации случайных процессов системы, регистрируемых в режиме ее функционирования. В первой задаче определяется оператор системы; она известна как задача идентификации. Вторая обратная задача связана с отысканием статистических характеристик внешних возмущений , действующих на систему, внутренних помех 
и мест их локализации (идентификация возмущений и помех). К сожалению, одновременное решение этих двух задач невозможно [1,2, 3, 5].
Так, идентификация динамических характеристик может производиться лишь при наличии экспериментальных данных о сигналах и априорных сведений о внутренних помехах (необходимы в случаях, когда они коррелированы с внешними возмущениями). Во многих случаях данные о помехах могут быть получены априори только в режиме отладки систем при отсутствии внешних возмущений. Поэтому полученные в результате идентификации динамические характеристики системы могут отличаться от тех, которые соответствуют режиму функционирования системы.
При решении задачи идентификации помех необходимо иметь экспериментальные данные и знать динамические характеристики системы или ее звеньев. Очевидна необходимость использования метода итераций. Что касается методических вопросов идентификации возмущений и помех, действующих в сложных многомерных системах, в том числе с перекрестными связями, то удовлетворительного решения на сегодня нет.
Описание систем в частотной области оказывается более удобным и экономичным, особенно для стационарных систем. Здесь динамические характеристики и взаимная спектральная плотность не зависят от времени и возможно определение частотной характеристики идентифицированной системы по известным спектральным плотностям:
.
Однако при идентификации динамической системы, функционирующей задолго до момента анализа 
(накопление энергии к моменту ), возможно получение больших ошибок, связанных с влиянием погрешностей вычисления корреляционных функций, а затем и спектральных плотностей.
Основная сложность в решении уравнения идентификации связана с некорректностью задачи (даже при вычислении корреляционных функций и спектральных плотностей с высокой степенью точности). Действительно, импульсная переходная функция
.
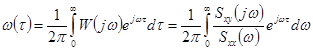При ошибке
вычисления взаимной корреляционной функции 
спектральная плотность также будет вычислена с ошибкой 
. Вместо истинной импульсной переходной функции получим ее оценку
;
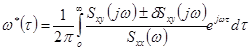норма ошибки
.
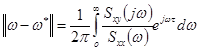Как видим, норма ошибки может быть как угодно большой в зависимости от распределения спектральной плотности 
. Задача идентификации является не корректной. Для классически корректно поставленной задачи произвольно бесконечно малым возмущениям исходных данных должны соответствовать бесконечно малые возмущения решения. Если и 
имеют нули одинаковой кратности в какой-либо конечной точке оси 
, то погрешность решения также может быть значительной. К сожалению, решение уравнения идентификации в частотной области принципиально возможно лишь для непрерывно и длительно функционирующих систем со стационарными или стационаризируемыми (нестационарные сигналы, корреляционные функции которых определяются двойным усреднением: сначала – по времени определяется 
, а затем – по ансамблю 
) входными сигналами. Даже в этом случае возникают трудности из-за плохой обусловленности решения и связанной с этим некорректностью задачи. Корректность решения, в первую очередь, зависит от распределения спектральной плотности входного сигнала.
Для восстановления идентифицируемых характеристик в случаях, когда начало идентификации совпадает с началом функционирования системы, частотные методы, строго говоря, не применимы (нет возможности перехода к спектральным плотностям).
Для колебательных систем весьма актуально решение уравнения идентификации
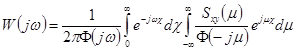
для системы, находящейся под воздействием стационарных или стационаризируемых входных сигналов. Известно, корректность решения связана с выполнением условий:
- спектральная плотность
должна содержать четные степени , если степень числителя 
меньше степени знаменателя 
;
- знаменатель не должен иметь действительных корней и превращаться в нуль, или быть достаточно близок к нему;
- числитель не должен иметь действительных корней;
- коэффициенты полиномов и должны быть действительными.
Точность идентификации будет тем больше, чем больше отличается от нуля при всех действительных в диапазоне исследуемых частот.
При решении ряда задач виброзащиты [6,7] нами использовался приводимый ниже алгоритм решения уравнения идентификации (система на подвижном основании со стационарным или стационаризируемым сигналом; моменты начала идентификации и функционирования совпадают).
1. Определение по экспериментальным данным корреляционной функции входного сигнала и взаимной корреляционной функции 
.
2. Вычисление .
3. Представление в виде ;
и – полиномы относительно , содержащие только четные степени относительно частоты ( – четная функция).
4. Определяется частотная характеристика
так называемого формирующего фильтра (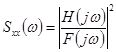
). Для этого и разлагаются на множители; отбираются в полученных разложениях множители, соответствующие корням, расположенным в верхней полуплоскости комплексной переменной 
, добавляются к таким множителям 
(
– коэффициент при 
в разложении полинома ) и 
(
– коэффициент при 
в разложении полинома ).
5. Определение спектральной плотности 
по корреляционной функции 
.
6. Наконец, определяется
.
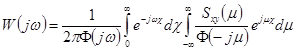Справедливо:
,
.
Предложенный алгоритм прошел положительную апробацию при определении характеристик, как объекта, так и оператора по данным нормального функционирования транспортной эргатической системы [4, 6-9].
Рецензенты:
Родионов Ю.В., д.т.н., профессор, заведующий кафедрой «Эксплуатация автомобильного транспорта», декан автомобильно-дорожного института ПГУАС, г. Пенза;
Кошев А.Н., д.х.н., профессор, профессор кафедры «Информационно-вычислительные системы» Пензенского государственного университета архитектуры и строительства, г. Пенза.