В концепции активных баз данных (АБД) возникающие в базе данных события обрабатываются активными правилами – объектами специального вида, которые хранятся наравне с обычными данными. Если обработка одного события подразумевает генерацию другого события, то последнее становится промежуточным. Особенностью активных правил является отсутствие ограничения на количество промежуточных событий, если активные правила остаются корректными не конфликтуют друг с другом.
Система управления активными базами данных (СУАБД) имеет в своём составе специальную подсистему статической проверки, которая при создании очередного активного правила выявляет возможные сценарии взаимодействия с другими правилами, выбирает среди них конфликтные и определяет параметры событий, приводящих к ним. Статическая проверка позволяет определить, могут ли правила работать корректно вне зависимости от обрабатываемых событий или же могут возникнуть такие события, обработка которых приведёт к нежелательным результатам.
Проблема эффективности статической проверки имеет два аспекта. Один состоит в отсутствии чётко сформулированных критериев корректности правил. Другой относится к математической модели, с помощью которой данные критерии должны проверяться.
Терминальность и конфлюентность набора активных правил
Из-за отсутствия ограничения на количество промежуточных событий в случае активных правил остро стоит проблема зацикливания. Она заключается в том, что при обработке некоторого события некорректные правила начинают бесконечно вызывать друг друга через одинаковые повторяющиеся промежуточные события.
В работах, посвящённых статической проверке правил, широко используется понятие терминальности (termination), которое определяет свойство набора правил, означающее, что для них невозможно зацикливание, какое бы событие ни возникло.
Также в дополнение к терминальности часто упоминается понятие конфлюентности (confluence), означающее невозможность возникновения ситуации, когда инициированные одним событием правила одновременно пытаются изменить один объект базы данных и тем самым конфликтуют друг с другом. Данную ситуацию можно назвать состоянием гонки по аналогии с похожи конфликтом транзакций в системе управления базами данных (СУБД).
Терминальные и конфлюентные правила являются корректными и не вступают в конфликты друг с другом при обработке событий.
На сегодняшний день существует несколько подходов к проверке терминальности, реже уделяется внимание проблеме конфлюентности.
Наиболее известный подход к описанию потенциальных взаимодействий правил предложен в работе [2]. Он основан на принципе инициируемости вызова правил. В качестве критерия инициируемости использовано совпадение типов генерируемого одним правилом и обрабатываемого другим событий. В рамках данного подхода в качестве модели описания взаимодействия правил использован граф срабатываний (triggering graph). Его вершины соответствуют активным правилам, а дуги означают инициируемость правил. В качестве критерия терминальности правил подразумевалась ацикличность графа срабатываний.
Основным недостатком описанного подхода является то, что вызов активных правил не всегда приводит к запуску действия, так как контекст события должен удовлетворять условию правила. Данное обстоятельство означает, что наличие путей в графе срабатывании не гарантирует, что соответствующий вариант последовательного инициирования правил возможен.
В качестве усовершенствования описанного подхода в ряде исследований [2, 3, 5, 6] рассматривается возможность использования графа активации (activation graph), в котором в качестве критерия инициируемости использовалось пересечение области значений инициирующего правила с областью определений инициируемого.
Несмотря на то что использование графа активации позволяет повысить точность критерия терминальности, наличие пути от одного правила к другому в графе не гарантирует возможность опосредованного инициирования, так как в нём не учитывается то, что инициирующее правило само может быть инициируемым.
В работе [4] рассмотрено моделирование опосредованного инициирования правил, заданных в виде вещественных функций. Авторами было показано, что в случае инициирования область значений активного правила меняется в зависимости от того, какая последовательность правил приводит к его запуску. В данной работе решалась задача проверки терминальности для правил с вещественными параметрами путём решения системы уравнений, построенной на основе арифметических функций, описывающих выходные параметры правил. Математической модели для статической проверки правил общего типа предусмотрено не было.
Граф областей значений активных правил
Для проверки терминальности и конфлюентности набора правил в рамках статической проверки предложена модель описания потенциальных взаимодействий правил в виде графа областей значений GR. Вершины графа соответствуют оценкам областей значений правил. Если область значений одного правила пересекается с областью определений другого, то между вершинами, сопоставленными с соответствующими оценками, в графе присутствует дуга ![]() :
:
![]()
где vi – оценка области значений потенциально инициирующего правила, vj – оценка области значений потенциально инициируемого правила, ϕ(r,C) – область значений правила r относительно области определения, входящей в C, y (v) – множество правил, инициируемых событиями из множества v.
Множество областей значений правил не известно заранее, однако может быть определён порядок последовательного добавления в него новых элементов. В случае графа областей значений добавление вершин может осуществляться одновременно с добавлением входящих дуг, поэтому весь процесс может быть описан как алгоритм построения графа GR., представленный на рисунке 1.
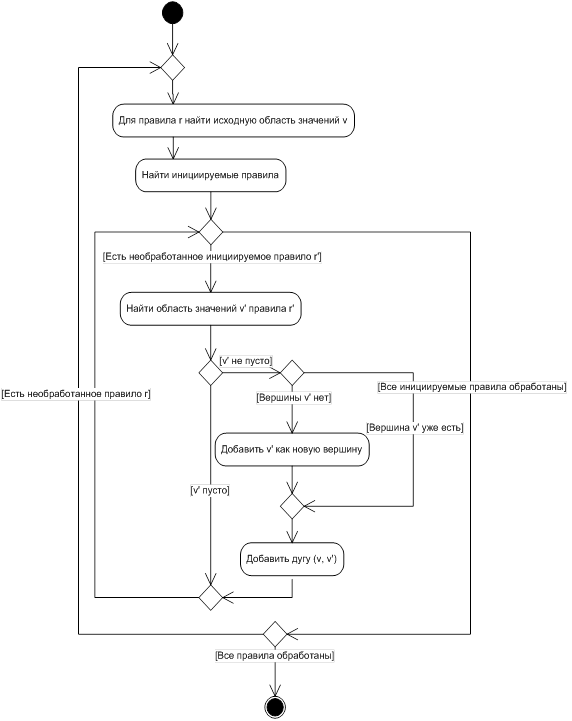
Рис. 1. Алгоритм построения графа областей значений.
Терминальность правил может определяться путём проверки ацикличности графа областей значений [1]. По нему предлагается определить, с какого правила начнётся зацикливание, какие правила опосредованно в нём будут участвовать, какие правила будут выполнены непосредственно перед зацикливанием, а также области значений параметров всех правил при этом.
Наличие нескольких пересекающихся циклов означает, что правило может опосредованно вызывать себя несколькими способами.
Неконфлюентность правил также может быть проверена с помощью графа областей значений. Состояние гонки возникает, когда с одним событием связаны две цепочки запусков правил и они выполняют противоречащие друг другу действия с одним и тем же объектом.
Программные средства, реализующие статическую проверку на основе графа областей значений, были реализованы в электронной карте города Пензы, обслуживаемой МУП «Объединённая городская служба архитектуры, градостроительства и технической инвентаризации». Статическая проверка была разбита на два этапа: построение графа срабатываний и построение графа областей значений. Построение графа срабатываний требует значительно меньше времени вычислений, так как не включает процедуру оценивания, и использовалось для того, чтобы выявить заведомо не связанные с другими правила и исключить их из дальнейшей проверки.
Пример графа областей значений приведён на рисунке 2.
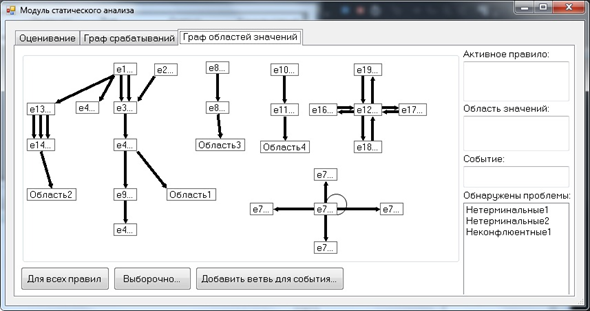
Рис. 2. Граф областей значений для разработанных активных правил
Граф областей значений был построен для 28 активных правил, обрабатывающих события, которые возникают при работе с адресами и полигонами земельных участков в электронной карте. Было выявлено две группы нетерминальных правил и одна неконфлюентных. В обоих случаях нетерминальности после исправления соответствующих активных правил оказалось, что возможное число промежуточных событий превосходит допустимый лимит запуска триггеров в используемой СУБД, оставаясь при этом конечным. Таким образом, триггеры не могли быть использованы для решения тех задач, что и разработанные активные правила.
Заключение
Введение понятия графа областей значений позволяет решать основные задачи статического анализа: проверку правил на терминальность и конфлюентность. Также с его помощью может осуществляться выявление и исследование возможных сценариев взаимодействия правил при обработке событий.
Рецензенты:
Макарычев П.П., д.т.н., профессор, заведующий кафедрой «МОиПЭВМ» ФГБОУ ВПО «Пензенский Государственный Университет», г. Пенза;
Зинкин С.А., д.т.н., профессор, профессор кафедры «Вычислительная техника» ФГБОУ ВПО «Пензенский Государственный Университет», г. Пенза.



